Задачи и Упражнения по Общей Астрономии<< 5. Астрономическая рефракция | Оглавление | 7. Суточное движение Солнца >>
6. Движение Земли вокруг Солнца
Как известно, Земля обращается по своей орбите вокруг Солнца. Для нас,
находящихся на поверхности Земли людей, такое годовое движение Земли
вокруг Солнца заметно в виде годового перемещения Солнца на фоне звезд.
Как мы уже знаем, путь Солнца среди звезд является большим кругом небесной
сферы и называется эклиптикой. Значит, эклиптика является небесным отражением
орбиты Земли, поэтому плоскость орбиты Земли называют еще плоскостью эклиптики.
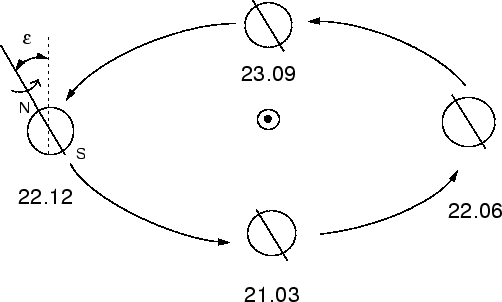
Ось вращения Земли не перпендикулярна плоскости эклиптики, а отклоняется от
перпендикуляра на
угол
. Благодаря этому на Земле происходит смена времен
года (см. рис. 12). Соответственно, и плоскость земного экватора наклонена
на этот же угол к плоскости эклиптики. Линия пересечения плоскости
земного экватора и плоскости эклиптики сохраняет (если не учитывать
прецессию) неизменноое положение в пространстве. Один ее конец указывает на
точку весеннего равноденствия, другой - точку осеннего равноденствия. Эти
точки неподвижны относительно звезд (с точностью до
прецессионного движения!) и вместе с ними участвуют в суточном вращении.
Вблизи 21 марта и 23 сентября Земля расположена относительно Солнца таким образом, что граница света и тени на поверхности Земли проходит через полюса. А поскольку каждая точка на поверхности Земли совершает суточное движение вокруг земной оси, то ровно половину суток она будет на освещенной части земного шара, а вторую половину - на затененной. Таким образом, в эти даты день равен ночи, и они называются соответственно днями весеннего и осеннего равноденствий. Земля в это время находится на линии пересечения плоскостей экватора и эклиптики, т.е. в точках весеннего и осеннего равноденствий, соответственно.
Выделим еще две особенные точки на орбите Земли, которые называются точками солнцестояний, а даты, на которые приходится прохождение Земли через эти точки, днями солнцестояний.
В точке летнего солнцестояния, в которой Земля бывает вблизи 22 июня (день летнего солнцестояния), северный полюс Земли направлен в сторону Солнца, и большую часть суток любая точка северного полушария освещена Солнцем, т.е. в эту дату день - самый длинный в году.
В точке зимнего солнцестояния, в которой Земля бывает вблизи 22 декабря (день зимнего солнцестояния), северный полюс Земли направлен в сторону от Солнца, и большую часть суток любая точка северного полушария находится в тени, т.е. в эту дату ночь - самая длинная в году, а день - самый короткий.
Из-за того, что календарный год по продолжительности не совпадает с периодом
обращения Земли вокруг Солнца, дни равноденствий и солнцестояний в разные годы
могут приходиться на разные дни (
один день от названных выше дат).
Однако в дальнейшем при решении задач мы будем пренебрегать этим и считать,
что дни равноденствий и солнцестояний всегда приходятся на указанные выше даты.
6.1. Видимое годовое движение Солнца
Перейдем от реального движения Земли в пространстве к видимому движению Солнца
для наблюдателя, находящегося на широте 
, . В течение года центр Солнца
движется по большому кругу небесной сферы, по эклиптике, против часовой
стрелки. Поскольку плоскость эклиптики в пространстве неподвижна относительно
звезд, то эклиптика вместе со звездами будет участвовать в суточном вращении
небесной сферы. В отличие от небесного экватора и небесного меридиана эклиптика
будет менять свое положение относительно горизонта в течение суток.
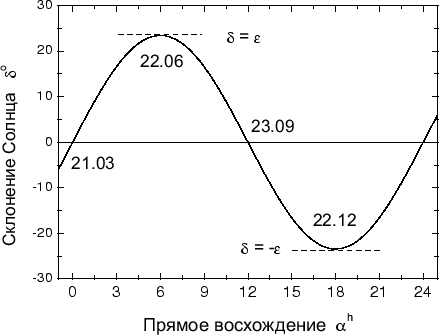
Как изменяются координаты Солнца в течение года? Прямое восхождение
изменяется от 0 до 24h, а склонение
изменяется от -
до +. Лучше всего это можно увидеть на
небесной карте экваториальной зоны (рис. 13).
Для четырех дней в году мы знаем координаты Солнца точно. Ниже в таблице даны эти сведения.
В таблице указана также полуденная (в момент верхней кульминации) высота
Солнца на эти даты. Для того, чтобы вычислить высоту Солнца в моменты
кульминаций на любой другой день года, нам необходимо знать
в этот день:
Таким образом, перед нами встает задача научиться приближенно рассчитывать координаты Солнца на любой день года.
В первом приближении Солнце движется по эклиптике равномерно: за 365d
проходит 360o, примерно 1o в сутки, а точнее 59'.2. Как будут при
этом меняться
и
? Точный ответ можно получить
только из решения сферических треугольников, и в данном курсе мы этим заниматься
не будем. Важно понять, что даже при строго равномерном движении Солнца по
эклиптике (что, вообще говоря, не так из-за эллиптичности земной орбиты: вблизи
перигелия Земля, а соответственно и Солнце среди звезд, движется быстрее, чем в
афелии), изменение экваториальных координат Солнца происходит неравномерно.
Мы пренебрежем здесь неравномерностью в изменении прямого восхождения, и будем
считать, что суточное изменение 
= 59'.2. Склонение быстрее всего
изменяется вблизи равноденствий, примерно 
в сутки в течение 30d
до и в течение 30d после равноденствия. Медленнее всего изменения склонения
Солнца происходят вблизи солнцестояний: 
в сутки в течение 30d
до и в течение 30d после солнцестояния. В промежутках скорость изменения
склонения Солнца приблизительно 
в сутки.
Подробнее скорость изменения склонения в разное время года представлена в
таблице 2.
| Даты |  /сутки |
| 19 февраля - 20 апреля | + 0o.4 |
| 21 апреля - 22 мая | + 0o.3 |
| 23 мая - 22 июня | + 0o.1 |
| 22 июня - 22 июля | - 0o.1 |
| 23 июля - 21 августа | - 0o.3 |
| 22 августа - 23 октября | - 0o.4 |
| 24 октября - 22 ноября | - 0o.3 |
| 23 ноября - 22 декабря | - 0o.1 |
| 22 декабря - 21 января | + 0o.1 |
| 22 января - 18 февраля | + 0o.3 |
Этой таблицей мы будем пользоваться, чтобы вычислять склонение Солнца на любой день года.
Задачи
20. Какова максимальная высота Солнца в Казани (
)
4 октября? Рефракцию не учитывать.
Решение: Максимальную высоту Солнце имеет в момент верхней кульминации. Для того, чтобы ее рассчитать, нам необходимо приближенно вычислить склонение Солнца 4 октября. Делается это следующим образом:
1) Необходимо определить ближайшую к данной дату, на которую склонение Солнца
нам известно точно, т.е. либо день солнцестояния, либо день равноденствия, и
зафиксировать значение склонения Солнца в этот день.
В данном случае это день осеннего равноденствия 23 сентября и
в этот день равно 0o00'.
2) Рассчитать количество дней, прошедших с этой даты до дня, на который нам необходимо узнать склонение Солнца. В нашем случае это 11 дней, 7 дней в сентябре и 4 дня в октябре.
3) Выяснить по таблице 3 скорость изменения склонения в этот период. Это -0o.4 день.
4) Сосчитать полное изменение склонения за этот период. Оно составляет
.
5) Прибавить полученное изменение склонения к известному зафиксированному
значению склонения в том случае, если рассматриваемая дата идет позже
даты, от которой мы считаем склонение. Если мы ищем склонение Солнца на дату
предшествующую той, от которой мы считаем склонение Солнца, то полное изменение
склонения необходимо вычесть. В нашем случае мы вели отсчет от 23 сентября и
в этот день. Следовательно, склонение Солнца
4 октября будет суммой склонения 23 сентября и изменением склонения за период
с 23 сентября по 4 октября
.
Заметим, что точное значение склонения на 4 октября 2002 г. составляет
-4o 12'.
6) Рассчитать высоту Солнца в верхней кульминации по формуле (10). hmax= -4o 24' + 90o-55o47' = 29o 49'
21.Какова максимальная высота Солнца в Казани (
)
8 февраля? Рефракцию не учитывать.
Решение:
1) Необходимо определить ближайшую к данной дату, на которую склонение Солнца
нам известно точно, т.е. либо день солнцестояния, либо день равноденствия, и
зафиксировать значение склонения Солнца в этот день.
В данном случае это день весеннего равноденствия 21 марта и
в этот день равно 0o00'.
2) Рассчитать количество дней, прошедших с этой даты до дня, на который нам необходимо узнать склонение Солнца. В нашем случае это 41 день, 20 дней в феврале и 21 день в марте.
3) Выяснить по таблице 3 скорость изменения склонения в этот период. Это +0o.4 день с 19 февраля по 21 марта и +0o.3 в день с 8 февраля по 19 февраля.
4) Сосчитать полное изменение склонения за этот период. Оно составляет
.
5) Прибавить полученное изменение склонения к известному зафиксированному
значению склонения в том случае, если рассматриваемая дата идет позже
даты, от которой мы считаем склонение. Если мы ищем склонение Солнца на дату
предшествующую той, от которой мы считаем склонение Солнца, то полное изменение
склонения необходимо вычесть. В нашем случае мы вели отсчет от 21 марта и
в этот день. Следовательно, склонение Солнца
8 февраля будет разностью склонения 21 марта и изменением склонения за период
с 8 февраля по 21 марта
(точное значение склонения Солнца на 08.02.2002 -15o 07').
6) Рассчитать высоту Солнца в верхней кульминации по формуле (10): hmax= -15o 18' + 90o-55o47' = 18o 55'. Необходимо отметить, что если бы мы стали вычислять склонение Солнца от 22 декабря, мы получили бы несколько иной результат из-за того, что наши вычисления приближенные.
22. Какова максимальная высота Солнца в день Вашего рождения?
23. На какой широте 22 июня в момент нижней кульминации нижний край Солнца лежит точно на горизонте? Учесть рефракцию.
Решение:.
Будем искать широту места на основе соотношения между высотой светила в
нижней кульминации, его склонением и широтой места наблюдения:
В этой формуле под высотой светила в момент нижней кульминации имеется в виду высота центра истинного или теоретического (без учета рефракции) Солнца. А в условиях задачи нам дана высота, равная нулю, нижнего края наблюдаемого (с учетом рефракции) Солнца. Следовательно, высота центра наблюдаемого Солнца больше на величину его углового радиуса
. А высота центра теоретического Солнца
меньше высоты центра наблюдаемого Солнца на величину рефракции
.
Следовательно, она должна быть рассчитана по формуле
Получаем:
откуда
Склонение Солнца 22 июня нам известно,
. Заметим, что это склонение центра истинного Солнца.
Вычисления дают
.
24. Какова высота верхнего края Солнца в меридиане в день летнего
солнцестояния в Санкт-Петербурге (
)? Учесть рефракцию.
25. Как глубоко опускается центр Солнца под горизонт в полночь 22
декабря в Архангельске (
)?
<< 5. Астрономическая рефракция | Оглавление | 7. Суточное движение Солнца >>
|
Публикации с ключевыми словами:
задача - общая астрономия - Небесная сфера - системы координат - суточное вращение - рефракция - Сумерки - время - движение планет - расстояние - звезды - галактика
Публикации со словами: задача - общая астрономия - Небесная сфера - системы координат - суточное вращение - рефракция - Сумерки - время - движение планет - расстояние - звезды - галактика | |
См. также:
Все публикации на ту же тему >> | |
