Спиральная галактика NGC 23. Фотометрия и кинематика
<< 1. Введение | Оглавление | 3. Анализ фотометрических данных >>
- 2.1 Определение параметров диска по фотометрическим данным
- 2.2 Определение параметров диска по кинематическим данным
2. Выбор параметров диска
Одним из важных этапов при обработке как кинематических, так и фотометрических данных является правильный выбор ориентации галактики. Необходимо определить 4 основных параметра:1) положение центра диска;
2) позиционный угол большой оси диска;
3) наклонение плоскости диска к лучу зрения;
4) среднюю лучевую скорость галактики (скорость центра).
Если определение 4-го параметра возможно только по полю скоростей, то определение первых трех может быть произведено как по фотометрическим, так и по кинематическим данным.
2.1 Определение параметров диска по фотометрическим данным
Для определения параметров ориентации диска по фотометрическим данным существует несколько методов.Самый простой метод (без применения Фурье-анализа) - определение параметров эллиптических изофот. Для этого проводится поверхностная фотометрия галактики, затем анализируется поведение параметров эллиптических изофот (размеры осей и позиционного угла большой оси эллипса) в зависимости от расстояния от центра, исходя из чего можно определить первые три параметра. Наличие мощных спиральных ветвей искажают параметры изофот, что может привести к неточному определению ориентации галактики.
Методы, основанные на Фурье-анализе, позволяют в ряде случаев уточнить параметры диска. Ошибка в каждом из параметров ориентации влияет на определенную гармонику (гармоники), что позволяет выяснить, какой из параметров определен неточно. Например: если имеется диск с не слишком сильными спиральными ветвями, то при неправильном задании угла наклона, фаза второй гармоники ляжет либо точно вдоль большой оси диска (если заданный угол наклона меньше реального -- тогда в каждом кольце соответствующая яркая часть диска будет занимать только симметричные области вблизи большой оси, при этом предполагается, что яркость диска падает к краю), либо вдоль малой, если заданный угол наклона больше реального -- прямо противоположная ситуация. Разумеется, мощная двухрукавная спираль будет искажать картину -- при мощных спиральных ветвях фаза второй гармоники может ложиться на них в достаточно широком интервале углов наклона.
Довольно оригинальный метод был предложен недавно О.В.Хоружим [11] для определения позиционного угла диска и угла наклона к лучу зрения при известном положнии центра. На первом этапе устанавливается произвольный позиционный угол и нулевой угол наклона. После этого производится рассчет Фурье-гармоник. Тогда, очевидно, фаза второй гармоники будет представлять собой зависимость эффективного позиционного угла от радиуса. При этом участки, где спирали не очень сильны, будут выглядеть радиальными прямыми линиями, являющимися отрезками большой оси диска галактики, что позволяет с точностью до 0.5-1 градуса выставить значение позиционного угла. После установки позиционного угла начинаем менять наклонение к лучу зрения. В какой-то момент эти отрезки большой оси резко переместятся на малую ось (см. выше). Этот момент перехода соответствует правильному значению угла наклонения, который таким образом можно определить с точностью 2-3 градуса.
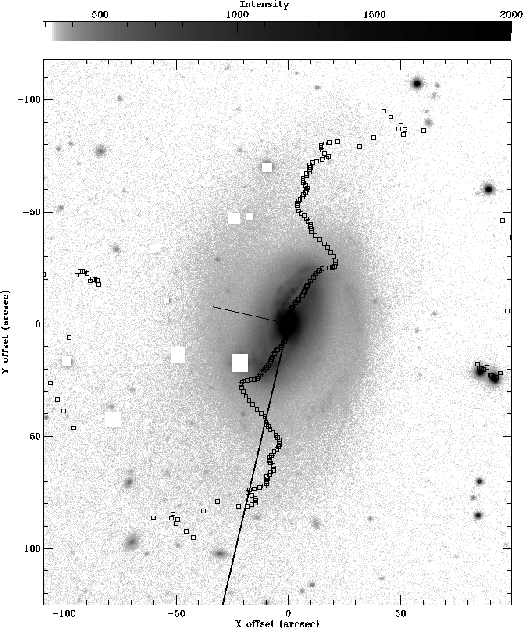 |
| Рис. .1 Изображение галактики NGC 23 в фильтре R (JKT), на которое наложена фаза второй Фурье-гармоники, рассчитанная в предположении нулевого угла наклона. Она показывает зависимость позиционного угла от радиуса, определенную формально без учета влияния спиралей и других морфологических составляющих галактики. |
NGC 23 имеет достаточно сложную морфологию и мощные спиральные ветви,
в связи с чем параметры,
определенные по изображениям с телескопа JKT, на которых видны очень
далекие от центра области галактики, отличаются от параметров согласно
каталогу RC3 (![]() ,
, ![]() )
и составляют: наклонение
)
и составляют: наклонение
![]() ,
позиционный угол большой оси
,
позиционный угол большой оси
![]() .
Выбранные параметры совпадают с параметрами, предложенными в работе [1]
.
Выбранные параметры совпадают с параметрами, предложенными в работе [1]
![]() в пределах ошибок.
При этом различие с параметрами из RC3 вызвано способом их определения в этом
каталоге. В каталоге RC3 параметры определялись, основываясь на изображениях
галактики на картах Паломарского обзора. На этих изображениях внешняя
часть диска галактики оказывается под пределом чувствительности фотопластинки,
а внешние части спиральных ветвей остаются видимыми. Они создают
видимую иллюзию поворота всей галактики.
в пределах ошибок.
При этом различие с параметрами из RC3 вызвано способом их определения в этом
каталоге. В каталоге RC3 параметры определялись, основываясь на изображениях
галактики на картах Паломарского обзора. На этих изображениях внешняя
часть диска галактики оказывается под пределом чувствительности фотопластинки,
а внешние части спиральных ветвей остаются видимыми. Они создают
видимую иллюзию поворота всей галактики.
2.2 Определение параметров диска по кинематическим данным
Существует несколько методов для определения параметров ориентации галактики по кинематическим данным.Исторически первый метод - определение позиционного угла и угла наклона диска по нескольким кинематическим разрезам, проходящим через центр галактики. Для этого берутся несколько разрезов, сделанных под разными позиционнными углами и депроецируются в предположении чисто кругового движения согласно известным тригонометрическим формулам. При правильных параметрах ориентации депроецированные кривые вращения совпадут [2]. Этот метод не принимает во внимание отклонения от кругового движения, в частности, возмущения скорости в спиральной волне.
При анализе двумерных кинематических данных (полей лучевых скоростей) Фурье-методами возможны следующие пути определения параметров галактики:
1) Минимизация отклонений от кругового вращения. При этом ищутся такие
параметры диска, при которых отклонения от кругового вращения
минимальны. Этот метод по сути является обощением вышеописанного
метода на двумерные данные. Он также может дать сбой при мощных возмущениях
скоростей спиральными волнами плотности, поскольку 2-рукавная спираль
дает вклад в 1-ю, 2-ю и 3-ю Фурье-гармоники скорости [3], в результате чего
кривая вращения отличается от амплитуды ![]() -компоненты на
величину порядка скоростей некруговых движений.
-компоненты на
величину порядка скоростей некруговых движений.
2) Можно попробовать уточнить параметры, минимизируя отклонения от низких гармоник (0, 1, 2, 3). При этом 2-рукавная спираль будет учтена, но метод обладает невысокой устойчивостью, связанной с малыми значениями амплитуд всех гармоник, кроме первой, что также может вызвать произвол в определении параметров.
3) Исходя из физических свойств спиральной волны плотности,
можно потребовать минимизации среднего значения Фурье-гармоник по радиусу
(за исключением ![]() ), но это также может привести к ошибкам
в ряде случаев, к примеру, когда поле скоростей (и соответственно
гармоники) на больших расстояниях известно плохо.
), но это также может привести к ошибкам
в ряде случаев, к примеру, когда поле скоростей (и соответственно
гармоники) на больших расстояниях известно плохо.
Как показывает опыт, наилучшие результаты обычно дает подход, когда параметры, полученные с помощью минимизации на ЭВМ среднеквадратичного отклонения от кругового вращения, корректируются с учентом некруговых движений для каждой галактики индивидуально, поскольку спиральная структура в каждой галактике по-своему уникальна.
В NGC 23 кинематическое определение параметров влечет за собой
серьезные проблемы в связи с хорошей заполненностью данных только во
внутренних областях галактики, где оказывают сильное влияние спиральные
ветви и, возможно, бар.
То есть методы в автоматическом режиме минимизации на ЭВМ дают отличие на
![]() по позиционному углу и
по позиционному углу и ![]() по углу наклона, но в то же время
при установке вышеназванных параметров, определенных из фотометрии,
гармоники остаются в пределах, соответствующих правильной ориентации.
по углу наклона, но в то же время
при установке вышеназванных параметров, определенных из фотометрии,
гармоники остаются в пределах, соответствующих правильной ориентации.
<< 1. Введение | Оглавление | 3. Анализ фотометрических данных >>
|
Публикации с ключевыми словами:
галактика - кинематика галактик - фотометрия галактик - NGC 23 - конкурс
Публикации со словами: галактика - кинематика галактик - фотометрия галактик - NGC 23 - конкурс | |
См. также:
Все публикации на ту же тему >> | |