Астронет > 9.5 Устойчивость релятивистских звезд

по текстам по ключевым словам в глоссарии по сайтам перевод

Физические основы строения и эволюции звезд

<< 9.4 Общие свойства равновесия ... | Оглавление | 9.6 Несферические поля ... >>

9.5 Устойчивость релятивистских звезд

Точно также, как и в случае белых карликов, можно показать, что первый максимум на кривой $M(\rho_c)$ соответствует устойчивости (см. раздел; 7.2). Однако появление минимума $M(\rho_c)$ здесь уже не означает возврата к устойчивому состоянию. Оказывается, что в -ом экстремуме кривой $M(\rho_c)$ теряет устойчивость -я собственная мода радиальных колебаний.

Устойчивыми оказываются только звезды с $\rho_c<\rho_{c\;\max}$ . Однако они устойчивы только относительно малых возмущений. Сейчас мы докажем, что относительно достаточно больших возмущений неустойчиво любое равновесие (теорема Зельдовича).

Когда мы говорим, что при некотором $\rho_{c0}$ равновесие звезды устойчиво, то это значит, что любые неравновесные конфигурации с тем же числом барионов (т. е. с тем же ) имеют в окрестности нашего решения $M(\rho_c)>M(\rho_{c0})$ . Покажем, что при больших $\rho_c$ есть конфигурации с очень малой массой: $M\ll M(\rho_{c0})$ (при той же ), т. е. относительно больших возмущений всегда есть неустойчивость.

Напишем выражение для массы звезды, которое, как мы уже говорили, верно и для неравновесных конфигураций:

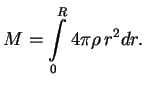
$\displaystyle M=\int\limits^R_0 4\pi\rho\,r^2dr.$

Число барионов

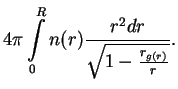
$\displaystyle 4\pi\int\limits^R_0 n(r){r^2dr\over{\sqrt{1-{r_{g(r)}\over r}}}}.$

Считаем, что для барионов справедливо уравнение состояния ультрарелятивистского газа:

$\displaystyle \rho\sim n^{4/3}.$

Пусть

$\displaystyle \rho=A/r^2,\,$ следовательно $\displaystyle ,\,r_g(r)/r=8\pi AG/c^2.$

Теперь получим, что

$\displaystyle M=$ const $\displaystyle \cdot N^{3/2}A^{1/2}(1-8\pi AG/c^2).$

Видно, что всегда можно выбрать

так, что

сколь угодно мало: $M\longrightarrow0$ при $\rho_c\longrightarrow\infty$ . Но ясно, что при конечных $\rho_c$ должны быть точки с малым

, что и доказывает неустойчивость любого состояния.

Оценим величину барьера, который надо преодолеть, чтобы звезда потеряла устойчивость. Будем работать в системе единиц $\hbar=c=1\,(G\ne 1)$ . В этих единицах размерность длины совпадает с размерностью обратной массы:

$\displaystyle [px]=[h]=[mcx],\qquad [x]=[h/mc]=[1/m].$

$\displaystyle [$ Энергия $\displaystyle ]=[E]=[mc^2]=[m]=[1/x],\,[Gm^2]=[e^2]=[Ex]=[x^0],$

т. е.

в этих единицах безразмерно.

В ультрарелятивистском газе энергия частицы $E=cp_F=n^{1/3}$ , следовательно, энергия звезды (масса)

$\displaystyle M=EN=Nn^{1/3},$

а радиус

$\displaystyle R\sim (N/n)^{1/3}.$

Теперь мы хотим, чтобы радиус конфигурации, состоящей из данного числа барионов, равнялся гравитационному радиусу звезды

$\displaystyle r_g=GM=GN(n)^{1/3}=N^{1/3}n^{-1/3}=R,$

т. е.

$\displaystyle n=N^{-1}G^{-3/2}.$

Чтобы сжать вещество до такой плотности, надо затратить энергию

$\displaystyle \Delta\,M=N^{2/3}G^{-1/2}-Nm.$

Отсюда видно, что при $N=N_{\mbox{крит}}(Gm^2)^{-3/2}$ барьера вообще нет. Это критическое число барионов соответствует максимальной равновесной массе, так как она может сколлапсировать без барьера (см. раздел 2.4). Для малых $N<N_{\mbox{крит}}$ относительная величина барьера растет:

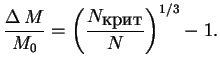
$\displaystyle {\Delta\,M\over{M_0}}=\left({N_{\mbox{крит}}\over N}\right)^{1/3}-1.$

Пример Земли: $M_{\oplus}=3\cdot10^{-6}\,M_\odot$ . Для того, чтобы перейти барьер, необходимо затратить энергию около 100 $\,M_{\oplus}c^2$ .

Однако в действительности эта оценка барьера не имеет смысла. Мы определили величину барьера из соображений подобия, т. е. считали, что звезда сжимается гомологически. А это вовсе не обязательно. Экономнее сжать в центре малую часть и заставить ее сколлапсировать. Потом на образовавшуюся черную дыру упадет все вещество. Беря все меньшее количество вещества, необходимо затрачивать все меньшее количество энергии, чтобы заставить его сколлапсировать.

Хотя для малых масс энергия мала, этот результат нельзя найти методом малых возмущений, так как $\delta E/E$ становится все больше и больше. Еще раз повторим, что плотность, до которой надо сжать вещество, с уменьшением массы возрастает (см. раздел 7.1):

$\displaystyle \rho=2\cdot10^{16}\,(M_\odot/M)^2\,[$ г/см $\displaystyle ^3].$

Таким образом, в классической ОТО барьер сводится к нулю. Однако, как обычно считают, квантовые эффекты становятся важными при $r_g<10^{-33}$ см, т. е. $m\sim 10^{-5}$ г. Здесь барьер $\sim mc^2=10^{16}\,$ эрг

Дж (это не так мало). Однако трудность здесь не в энергии, а в том, чтобы создать столь малый радиус. Надо различать явления необходимые (т. е. неизбежные) и возможные, по крайней мере, в принципе. Коллапс холодного вещества с массой $M>2\,M_\odot$ необходим, т. е. массивные звезды должны коллапсировать после исчерпания ядерного горючего. Можно сомневаться, сколько их в нашей Галактике:

или

. Но в принципе они должны существовать.

Те маломассивные черные дыры, о которых мы выше говорили, не обязательно существуют, так как они не получаются в результате эволюции звезд. Однако они могут в принципе образоваться на самых ранних стадиях расширения Вселенной из первичного вещества и приводить к интересным космологическим следствиям. Как показал Хокинг, такие черные дыры за счет квантовых процессов испускают тепловое излучение с эффективной длиной волны . При этом черная дыра, теряя массу, ``испаряется''.

Для черных дыр звездного происхождения $M\sim M_\odot$ эффект испарения ничтожен, увеличение массы в результате процессов аккреции окружающего газа гораздо сильнее. Для малых черных дыр, в особенности первичных, эффект велик, возникает множество интересных вопросов, которые однако, лежат за пределами данной книги.

<< 9.4 Общие свойства равновесия ... | Оглавление | 9.6 Несферические поля ... >>

Публикации с ключевыми словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы

См. также:

Туманность Кошачий глаз: переобработка данных космического телескопа

Кошачий глаз в ширину и глубину

Двойная звезда φ Персея

Эта Киля в рентгеновских лучах

Туманность Кошачий глаз

Планетарная туманность Стухшее Яйцо

Туманность Эскимос в обновленный телескоп Хаббла

Все публикации на ту же тему >>

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце