Колебания и волны. Лекции.
В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)Издательство Физического факультета МГУ, 2001 г. Содержание
Лекция 6
Волны на поверхности жидкости. Гравитационные волны. Капиллярные волны. Цунами. Внутренние волны. Акустические волны большой амплитуды. Линейный и нелинейный режимы распространения. Уединенные волны (солитоны).
Волны на поверхности жидкости. Гравитационные волны.
Многие из нас могут долго любоваться поверхностью моря или реки, по которой перекатываются волны. Рожденные ветром, они распространяются затем за счет силы тяжести. Такие волны называются гравитационными. Частицы воды совершают в них движение по круговым и эллиптическим траекториям ("вверх - вниз" и "вперед - назад" одновременно), поэтому такие волны (как и волны Лява) нельзя отнести ни к продольным, ни к поперечным. Гравитационные волны обладают рядом удивительных свойств, к анализу которых мы и приступим.
Пусть по поверхности водоема глубиной ![]() распространяется вдоль оси Ox
поверхностная гармоническая волна
распространяется вдоль оси Ox
поверхностная гармоническая волна
| (6.1) |
где ![]() - смещение поверхности воды вверх от равновесного горизонтального
положения, отмеченного на рис. 6.1 пунктиром. Будем считать, что
- смещение поверхности воды вверх от равновесного горизонтального
положения, отмеченного на рис. 6.1 пунктиром. Будем считать, что ![]()
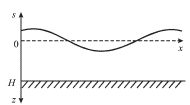 |
| Рис. 6.1. |
Предположим, что давление жидкости на глубине ![]() равно:
равно:
| (6.2) |
где ![]() - добавка к гидростатическому давлению
- добавка к гидростатическому давлению ![]() обусловленная волновым движением поверхности. Сделаем также предположение,
что
обусловленная волновым движением поверхности. Сделаем также предположение,
что
| (6.3) |
Выражение (6.3) записано в приближении, что возмущение давления вблизи
поверхности ![]() определяется дополнительным гидростатическим
давлением
определяется дополнительным гидростатическим
давлением ![]() связанным с изменением уровня жидкости при
распространении волны:
связанным с изменением уровня жидкости при
распространении волны:
| (6.4) |
причем с глубиной это возмущение должно убывать. Следовательно, функция
![]() с ростом
с ростом ![]() также должна убывать, при этом
также должна убывать, при этом ![]() Позже мы
докажем, что представление возмущения давления в виде (6.3) оправданно.
Позже мы
докажем, что представление возмущения давления в виде (6.3) оправданно.
Для описания волнового движения жидкости нам необходимо, во-первых, для
заданной частоты ![]() найти
найти ![]() то есть установить дисперсионную
зависимость
то есть установить дисперсионную
зависимость ![]() и, во-вторых, определить вид функции
и, во-вторых, определить вид функции
![]() Это можно сделать, если с учетом (6.2) записать уравнения Эйлера для
движения несжимаемой и невязкой жидкости в плоскости XOZ (см. уравнение
(3.30) в лекции по гидродинамике):
Это можно сделать, если с учетом (6.2) записать уравнения Эйлера для
движения несжимаемой и невязкой жидкости в плоскости XOZ (см. уравнение
(3.30) в лекции по гидродинамике):
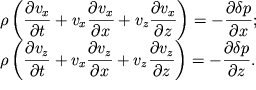 | (6.5) |
При записи (6.5) мы предполагаем, что движение частиц по оси Oy отсутствует.
Учтем далее, что членами ![]() и
и ![]() в силу их малости можно пренебречь. Тогда получаем
в силу их малости можно пренебречь. Тогда получаем
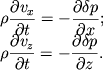 | (6.6) |
Эти уравнения дополним условием несжимаемости:
| (6.7) |
Уравнения (6.6) и (6.7) при заданных граничных условиях дают возможность
рассчитать ![]() и
и ![]() и, тем самым, получить решение
задачи о движении жидкости, включая движение ее поверхности.
и, тем самым, получить решение
задачи о движении жидкости, включая движение ее поверхности.
Продифференцируем первое из уравнений (6.6) по ![]() а второе - по
а второе - по ![]() :
:
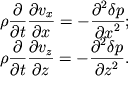 | (6.8) |
В левых частях этой системы уравнений изменен порядок дифференцирования.
Сложим теперь уравнения (6.8). Тогда с учетом (6.7) можем записать:
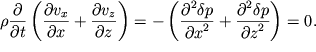 | (6.9) |
Уравнение
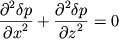 | (6.10) |
является знаменитым уравнением Лапласа, используемым во многих разделах физики. Поэтому его решение хорошо известно.
На поверхности водоема при ![]() граничным условием является равенство
(6.4), а на дне при
граничным условием является равенство
(6.4), а на дне при ![]() должно выполняться условие
должно выполняться условие ![]() из
которого с учетом второго уравнения (6.6) получаем:
из
которого с учетом второго уравнения (6.6) получаем:
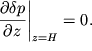 | (6.11) |
Подставим далее (6.3) в (6.10) и учтем, что 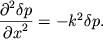
Тогда (6.10) примет вид:
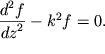 | (6.12) |
С методом решения таких уравнений мы познакомились в лекциях по колебаниям.
Используя подстановку ![]() получаем характеристическое
уравнение
получаем характеристическое
уравнение ![]() откуда
откуда ![]() и
общее решение (6.12) может быть записано в виде функции:
и
общее решение (6.12) может быть записано в виде функции:
| (6.13) |
при этом граничные условия для ![]() следующие:
следующие:
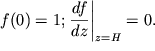 | (6.14) |
Подставляя (6.13) в (6.14), получаем:
| (6.15) |
Отсюда
![$ f(z) = {\displaystyle \frac{\displaystyle {\displaystyle {\displaystyle \rm ch}\;{\displaystyle \left[ {\displaystyle k(z - H)} \right]}}}{\displaystyle {\displaystyle ch(kH)}}}, $](http://images.astronet.ru/pubd/2002/04/09/0001175791/tex/formula1189.gif) | (6.16) |
где функция ![]() -гиперболический косинус.
-гиперболический косинус.
График функции ![]() изображен на рис. 6.2. Теперь осталось только
определить волновое число
изображен на рис. 6.2. Теперь осталось только
определить волновое число ![]() входящее в (6.1) и (6.3). Это можно сделать,
если сначала из (6.1) найти вертикальное ускорение частицы на поверхности
жидкости. При этом надо учесть, что положительные значения
входящее в (6.1) и (6.3). Это можно сделать,
если сначала из (6.1) найти вертикальное ускорение частицы на поверхности
жидкости. При этом надо учесть, что положительные значения ![]() соответствуют уменьшению
соответствуют уменьшению ![]() :
:
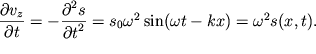 | (6.17) |
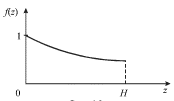 |
| Рис. 6.2. |
Подставим (6.17) в левую часть второго уравнения (6.6), а правую часть этого уравнения запишем, используя представление (6.3). Тогда получим
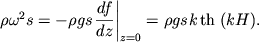 | (6.18) |
В (6.18) учтено, что ![]() Поэтому дисперсионное соотношение получается в виде:
Поэтому дисперсионное соотношение получается в виде:
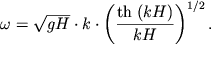 | (6.19) |
Обозначим ![]() Тогда
Тогда
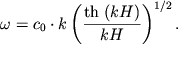 | (6.20) |
На рис. 6.3 эта зависимость изображена сплошной линией, а пунктиром показана
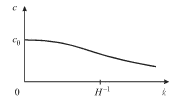
прямая ![]() Фазовая скорость волны
Фазовая скорость волны ![]() как
функция волнового числа показана на рис. 6.4.
как
функция волнового числа показана на рис. 6.4.
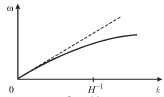 |  |
| Рис. 6.3. | Рис. 6.4. |
Таким образом, поверхностные гравитационные волны подвержены сильной
дисперсии. Эффект дисперсии ярко выражен у океанских волн, зарождающихся в
удаленных штормовых районах. Поскольку длинные волны (с меньшим ![]() ) движутся
быстрее, чем короткие, то они приходят к берегам раньше коротких на 1-2
дня.
) движутся
быстрее, чем короткие, то они приходят к берегам раньше коротких на 1-2
дня.
Эффект дисперсии может использоваться при определении места возникновения волн, прошедших до точки наблюдения чрезвычайно большие расстояния. Расстояние от штормового района до места, где волны фиксируют, подсчитывается по разности времен прибытия волн разной длины волны и, следовательно, разной частоты. Преобладающая частота прибывающих волн растет во времени, а длина пройденного пути находится по скорости изменения частоты. Так, по оценке, один из пакетов волн, наблюдавшихся в северной части Тихого океана, прошел половину окружности земного шара от Индийского океана по дуге большого круга, проходящей южнее Австралии.
Реальные волны, как уже говорилось раньше, представляют собой суперпозицию
волн, или волновые пакеты, которые движутся с групповой скоростью ![]() Скорость
Скорость ![]() группы меньше, чем скорости
группы меньше, чем скорости ![]() каждой
из волн в группе. Если рассматривать отдельную волну, то можно видеть, что
она перемещается быстрее, чем группа. При достижении фронта группы она
затухает, а ее место занимают волны, догоняющие группу с тыла.
каждой
из волн в группе. Если рассматривать отдельную волну, то можно видеть, что
она перемещается быстрее, чем группа. При достижении фронта группы она
затухает, а ее место занимают волны, догоняющие группу с тыла.
Фазовая скорость волны c, как следует из (6.20), зависит от параметра ![]() Поэтому различают волны глубокой и мелкой воды.
Поэтому различают волны глубокой и мелкой воды.
|
Публикации с ключевыми словами:
колебания - волны
Публикации со словами: колебания - волны | |
|
См. также:
| |