10.3 Определение расстояния Солнца от центра Галактики

Лекция 10. Вращение Галактики

10.3 Определение расстояния Солнца от центра Галактики

Формулы дифференциального вращения Галактики дают возможность по измеренным лучевым скоростям и расстояниям от Солнца звёзд и звёздных скоплений оценить расстояние Солнца от оси вращения Галактики. 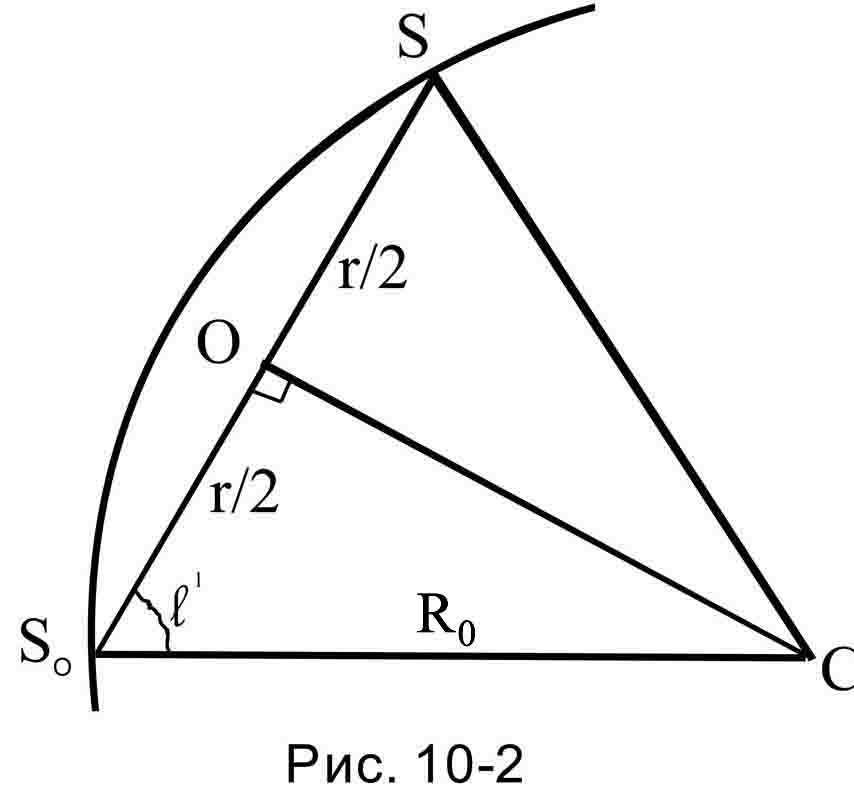Рассмотрим один из методов оценки величины R₀ по кинематическим данным, прежде всего - по лучевым скоростям. Используем для оценки R₀ выражение (10-9). Из него видно, что составляющая лучевой скорости, вызванная дифференциальным вращением Галактики, равна нулю для объектов, находящихся, как и Солнце, на расстоянии R₀ от центра Галактики. Понятно, что вращение здесь рассматривается в рамках той же модели, что и ранее - модели кругового баротропного вращения. Рис. 10-2 поясняет дальнейшие выкладки. На рисунке С - центр Галактики, S₀ отмечает положение Солнца, а S - положение объекта, также находящегося на расстоянии R₀ от оси вращения Галактики. Если мы найдем угол , который соответствует нулевой составляющей лучевой скорости, вызванной вращением Галактики, мы легко запишем выражение для определения R₀: Пусть мы выбрали группу объектов с почти одинаковыми расстояниями от Солнца. Построим график зависимости исправленных за движение Солнца в пространстве величин Δv_r от для этих объектов. Проведем через точки этой зависимости кривую, которую в случае небольшого интервала величин можно считать прямой, и найдем величину cos l , при котором уравнение этой прямой дает нуль. Это и будет значение cos l', которое надо подставить в выражение (10-20) для получения расстояния Солнца от центра Галактики. Так как в величины лучевой скорости входят пекулярные составляющие, разброс точек на зависимости Δv_r от cos l будет велик, и уравнение прямой следует получать методом наименьших квадратов. Реально выборку подходящих объектов делят на интервалы для разных значений r, и получают оценки R₀ по отдельности для каждой группы, которые потом усредняют.

Придумано много модификаций метода определения расстояния Солнца от оси вращения Галактики из кинематических данных. Эти методы можно найти в научной литературе. Для определения величины R₀ естественно использовать объекты большой светимости с наименьшей дисперсией остаточных скоростей. Такими объектами являются О и В звёзды, рассеянные звёздные скопления и классические цефеиды. Именно по этим объектам всегда и оценивалась эта величина. Так, по рассеянным звёздным скоплениям, шкала расстояний которых была согласована с тригонометрическими параллаксами Hipparcos, Локтин и Герасименко из Уральского университета, используя разные кинематические методы и данные о 170 объектах, получили оценку R₀ = 8.3 ± 0.3 кпк.

Ни один кинематический метод не учитывает возможные крупномасштабные отклонения от кругового движения центроидов. Поэтому результаты, получаемые кинематическими методами, нуждаются в уточнении. Независимым методом является, в частности, исследование изменения плотности некоторых объектов в направлении галактического центра. Так недавно, Макнамара и др. в исследовании изменения плотности переменных типа δ Щита и RR Лиры получили оценку R₀ = 7.9 ± 0.3 кпк. Эта оценка, как мы видим, мало отличается от приведенного выше значения, полученного по лучевым скоростям рассеянных звёздных скоплений. Можно считать, что расстояние Солнца от центра Галактики близко к величине 8 кпк.

Публикации с ключевыми словами: звездная астрономия Публикации со словами: звездная астрономия
См. также: Елене Вячеславовне Глушковой - 50 ! Конференция «Современная звездная астрономия - 2014» Конференция "Современная звездная астрономия" К 100-летию со дня рождения Петра Григорьевича Куликовского Лекции по Галактической Астрономии. 5–8 Лекции по Галактической Астрономии. 3–4 Лекции по Галактической Астрономии. 1–2 Все публикации на ту же тему >>