 Может ли наша Вселенная быть конечной и топологически сложной?
Может ли наша Вселенная быть конечной и топологически сложной?30.12.2003 20:14 | М. Е. Прохоров/ГАИШ, Москва
В самом начале 2003 года появились первые данные наблюдений реликтового фона, выполненные на космическом зонде WMAP (Wilkinson Microwave Anisotropy Probe). Впервые множество космологических параметров были измерены с необычайно высокой точностью. Но за несколько месяцев первые, самые важные результаты и предсказания были сделаны, восторги поутихли и любопытство ученых переместилось от полученных результатов к проблемам, оставшимся необъясненными.
Наблюдения
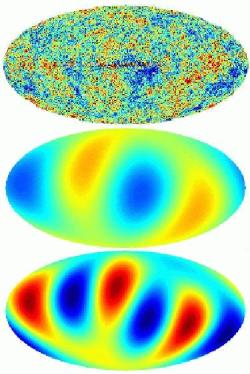
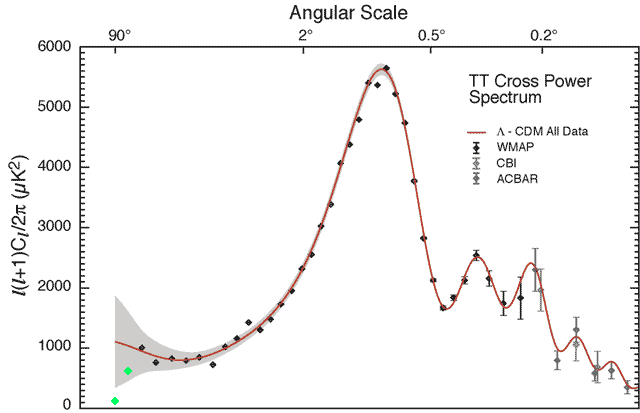
Одна из этих проблем - очень низкие амплитуды двух низших мультиполей (сферических гармоник) реликтового фона: квадруполя и октуполя. Эта проблема была известна и ранее, то только в очень точных данных WMAP она встала "во весь рост". На самом деле самой низкой сферической гармоникой является диполь. Он описывает поведение реликта на угловых масштабах равных 180o : в одном полушарии небесной сферы температура и яркость микроволнового фона оказывается выше, а в другой - ниже. К сожалению эту гармонику невозможно отделить от влияния на фон эффекта Допплера, связанного с движением наблюдателя. Вторая гармоника (квадруполь) описывает распределение флуктуаций температуры реликта на угловых масштабах в 90o, а третья гармоника (октуполь), соответственно на 60o (см. Рис. 1). Оказалось, что наблюдаемая амплитуда квадруполя составляет только 1/7 от предсказываемого теорией уровня, а амплитуда октуполя - 72% (см. Рис. 2). Это отклонение слишком велико и его трудно объяснить случайными флуктуациями наблюдаемого микроволнового космического фона. Некоторые исследователи начали предлагать ввести для объяснения этого отклонения "новую физику" (см., например, препринт astro-ph/0306597), другие с ними не соглашались (astro-ph/0306431). Пока, однако, никто не предложил какой-либо физический механизм, который привел бы к уменьшению амплитуд двух низших гармоник.
|
| Рис. 1. Карта анизотропии реликтового излучения по данным WMAP (вверху), ее квадруполь (в середине) и октуполь (внизу) из препринта astro-ph/0307282. |
|
|
Рис. 2.
Спектр мощности угловых распределений флуктуаций реликтового фонового
излучения по данным WMAP и некоторых других экспериментов. По вертикали
отложена амплитуда флуктуаций, по горизонтали номера гармоник (начиная
с l=2) или угловые масштабы. Черные точки - наблюдательные
данные, красная линия - предсказания теоретической модели для плоской
Вселенной, лучше всего согласующиеся с наблюдениями, серая полоса -
допустимая ошибка теоретических предсказаний. Слишком низкие значения
двух низших гармоник показаны зеленым цветом.
Низкая амплитуда только одного октуполя (l=3) недостаточно значима, но вместе с очень низким значением второй гармоники они становятся важным наблюдательным фактом. |
Топология
В работе, Люмине и др. опубликованной в Nature, такое решение предложено, только оно оказалось связанным не с физикой, а с геометрией, точнее с топологией.
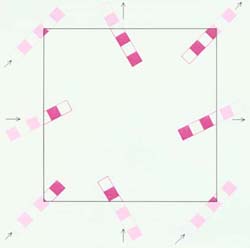
Основная суть этого решения заключается в том, что наша Вселенная имеет конечный объем и размеры, которые не может превышать длина волны самого крупномасштабного возмущения в таком Мире. А тот факт, что мы не видим каких-либо его границ, объясняется сложной топологией. Идея Вселенной со сложной топологией отнюдь не нова. Фридмановские модели обладают самыми простыми из возможных топологий: плоская и открытая модели по топологической структуре эквивалентны плоскости, а замкнутая модель - сфере (приведены двумерные аналогии). Следующая по сложности, после плоскости и сферы, фигура - тор. Только не надо его представлять в виде бублика, гораздо более подходящее для наших целей представление - прямоугольник у которого склеены противоположные стороны. Очень хорошая аналогия - экран некоторых игровых приставок: объект, уходящий за правую границу экрана, появляется слева, а ушедший вниз - сверху. При этом геометрия такого тора остается Евклидовой, т.е. параллельные линии не пересекаются, сумма углов треугольника равна 180o и т.д.
|
| Рис. 3. Двумерный тор. |
Чтобы получить трехмерный тор надо попарно склеить противоположные стороны прямоугольного параллелепипеда (бруска). В этом случае получится бесконечное пространство не имеющее границ, но с конечным объемом, и в какую бы стороны мы ни смотрели мы будем глядеть в затылок своим собственным изображениям.

|
| Рис. 4. Вид, открывающийся наблюдателю внутри трехмерного тора, похож на то, что можно увидеть в комнате, все стены, пол и потолок которой зеркальны; только изображение, в отличие от обычного зеркального отражения, не перевернуто. Луч зрения уходит, скажем, сквозь правую стену и возвращается из левой стены; поэтому, глядя направо, наблюдатель видит комнату так, как будто он смотрит на нее снаружи сквозь прозрачную левую стену (только при этом он видит в комнате своего двойника). Аналогичные картины возникают при взгляде вперед или вверх. Так как луч зрения при продолжении неограниченно пронизывает трехмерный тор, комната будет выглядеть как простирающаяся во все стороны бесконечная прямоугольная решетка. Но трехмерный тор не бесконечен, поскольку все видимые образы, составляющие бесконечную прямоугольную пространственную решетку, - изображения одного и того же предмета. |
Давайте посмотрим из каких фигур можно строить топологически сложные пространства. Условия, которые на них налагаются логичны и понятны.
- Тела свободно пересекают грани исходной фигуры (грань - не стенка): не должно оставаться не склеенных граней.
- В пространстве нет дыр и разрывов: грани склеиваются целиком, т.е. имеют одинаковую форму.
- Тела при пересечении грани фигуры не меняют своих размеров: склеиваемые грани должны быть одного размера (они склеиваются без растяжения).
- Тела при пересечении ребра или вершины не разрываются:
- соседние грани фигуры склеиваются с соответствующей парой соседних граней;
- сумма двугранных углов вокруг ребра должна составлять
2
 , а трехгранных углов у вершины - 4
, а трехгранных углов у вершины - 4 .
.
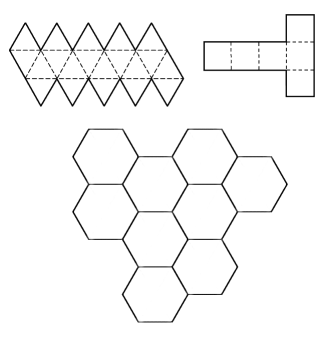
Построение пространства со сложной топологией можно представить себе и по другому: не как склейку граней одной фигуры, а как заполнение пространства бесконечным числом копий начальной фигуры. (Перечисленные выше ограничения для такой процедуры означают, что пространство заполняется копиями фигуры без зазоров и растяжений.) Процедура заполнения пространства имеет наглядную аналогию в двумерии - задачу о "паркете" (или "мозаике") - о мощении плоскости без зазоров одинаковыми геометрическими фигурами. Плоскость можно без зазоров покрыть треугольниками, параллелограммами и центрально-симметричными шестиугольниками.
|
| Рис. 5. Три возможных варианта покрытия плоскости правильными многоугольниками. |
Для заполнения трехмерного пространства пригодно также небольшое число фигур: параллелепипеды и шестигранные призмы. Из пяти правильных многогранников (так называемых Платоновых тел) для заполнения Евклидова пространства годится только куб (см. Рис. 6). Если для заполнения пространства используются фигуры (прямоугольные параллелепипеды, кубы, правильные шестигранные призмы) обладающие дополнительными симметриями, то соседние фигуры могут быть повернуты друг относительно друга (на 90o, 180o или 60o), что соответствует склейке граней фигуры с соответствующим поворотом. Разные "повороты" при склейке создают пространства с разными топологиями.
[Более подробно о таких пространствах со сложной топологией можно прочитать в статье "Какую форму имеет наша Вселенная".]
|
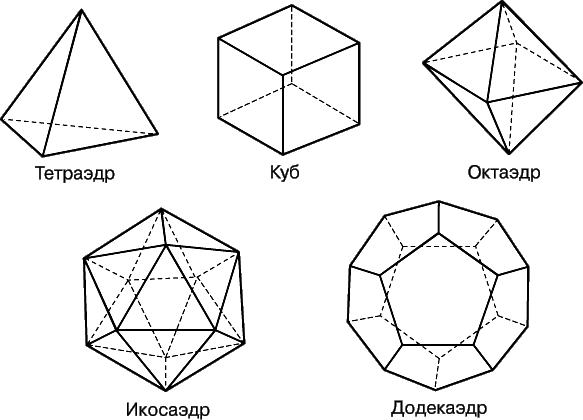
| Рис. 6. Правильные многогранники - Платоновы тела. Грани этих фигур являются одинаковыми правильными многоугольниками и в каждой вершине сходится одно и то же число граней. |
Искривленные пространства
А вот заполнить плоскость другими правильными многоугольниками не удастся. Например у правильного пятиугольника угол при вершине равен 108o. Если сложить три пятиугольника, то останется зазор в 36o, а если четыре, то они станут накладываться друг на друга (сумма углов при вершинах будет равна 432o, что превышает 360o). Для многоугольников с числом сторон большим шести наложение возникает уже при попытке сложить вместе три фигуры (поскольку углы правильного n-угольника равны 180o-360o/n).
|
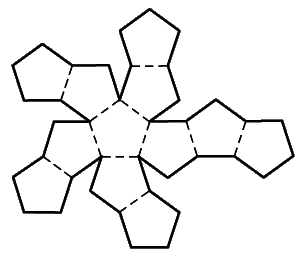
| Рис. 7. Попытка покрыть плоскость правильными пятиугольниками. |
Эта картина очень похожа на то, что получается при заполнении пространства додекаэдрами. Это правильные многогранники, у которых 12 граней, 20 вершин и 30 ребер, все их грани являются правильными пятиугольниками, а в каждой вершине сходятся три грани и, соответственно, три ребра (см. Рис. 6). Как при попытке сложить ребрами три таких фигуры, так и при совмещении вершин четырех многогранников остаются "щели".
Что изменится если попробовать выложить паркет не на плоской, а на кривой поверхности? Для того чтобы элементы паркета в разных местах поверхности оставались одинаковыми по форме поверхность должна обладать постоянной кривизной. В двумерном случае постоянной отрицательной кривизной обладают гиперболические поверхности, положительной - сферы, а плоскость является промежуточным случаем - поверхностью с постоянной нулевой кривизной. Примеры этих поверхностей показаны на Рис. 8.
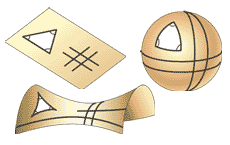
|
| Рис. 8. Двухмерные аналоги евклидовой, сферической и гиперболической геометрий. В плоском евклидовом пространстве параллельные прямые нигде не пересекаются, а сумма углов любого треугольника равна 180o. На сферической поверхности все параллельные пересекают друг друга, а сумма углов треугольников всегда больше 180o. На гиперболоиде сумма углов треугольника меньше 180o, а параллельные прямые расходятся. |
Прямыми на этих поверхностях являются кратчайшие линии, соединяющие пары точек. На сфере такими линиями являются дуги больших кругов (кругов, плоскости которых проходят через центр сферы). Соответственно, фигуры бывшие на плоскости треугольниками, квадратами и многоугольниками на сфере превращаются в сферические треугольники и многоугольники. Интересной особенностью этих фигур является зависимость суммы углов при их вершинах от размера фигуры (точнее от ее площади). Так у маленького сферического треугольника сумма углов только слегка превышает 180o, а у треугольника занимающего почти половину сферы она приближается к 360o (см. Рис. 9). На гиперболоиде наблюдается противоположная картина: сумма углов многоугольника меньше, чем на плоскости и убывает с ростом его размеров.

|
| Рис. 9. С увеличением размеров сферического треугольника его углы становятся более тупыми, а их сумма увеличивается. |
Если взять правильный пятиугольник на сфере, то при определенных размерах его углы станут равными 120o (а не 108o, как на плоскости) и три таких пятиугольника будут без зазоров стыковаться друг с другом, если их сложить вершинами. Более того, двенадцать пятиугольников такого размера без зазоров покрывают всю сферу. Эта фигура вам наверняка хорошо известна: некоторое время назад так шили футбольные мячи. (Сейчас их чаще всего собирают из двух типов фигур: пяти и шестиугольников.) По-другому, показанную фигуру можно представить, как проекцию ребер и граней правильного додекаэдра на описанную вокруг него сферу.
 |
 |
| Рис. 10. Футбольный мяч - сфера, собранная из двенадцати сферических пятиугольников. | |
Аналогичная картина получается при заполнении трехмерного пространства "трехмерными пятиугольниками" - додекаэдрами. Заполнить ими Евклидово пространство "без щелей" не удается. Но в пространстве положительной кривизны их углы (и двугранные углы при ребрах фигуры, и телесные при вершинах) с увеличением размеров фигуры растут таким образом, что в определенный момент все зазоры исчезают и 120 сферических додекаэдров (каждый из которых сам напоминает футбольный мяч) целиком заполняют поверхность трехмерной гиперсферы.

|
| Рис. 11. Сто двадцать сферических додекаэдров, полностью заполняющих трехмерную гиперсферу. |
[Не менее интересные результаты получаются и в гиперболических пространствах с отрицательной кривизной. Более подробно об этом можно прочитать в статье "Математика трехмерных многообразий".]
Вселенная, построенная из двенадцатигранников, обладает по крайней мере двумя преимуществами по сравнению с основанной на кубических торах.
- Додекаэдральная структура жесткая, в отличие от кубической, обладающей шестью степенями свободы (растяжения по каждой из трех осей и перекосы).
- Додекаэдральное пространство глобально однородно, его геометрия и наблюдаемый в нем спектр флуктуаций не зависят от положения наблюдателя внутри исходного многогранника.
Периодичность
Во вселенной (специально пишу это слово с маленькой буквы) конечного размера мы не можем создать структуру, масштаб которой превосходят ее размер. Склейка граней исходной фигуры или заполнение трехмерного пространства копиями исходной области приведут к тому, что в видимой нами безграничной Вселенной размеры структур и возмущений будут ограничены тем же масштабом.
А какие возмущения мы увидим на небе? Как они будут распределяться по небесной сфере во Вселенной со сложной топологией?
Если бы Вселенная не эволюционировала со временем, то все видимые нам копии исходного мира полностью совпадали бы друг с другом. Тогда во Вселенной построенной из кубов мы бы видели картину, показанную на Рис. 4. Каждый объект был бы окружен шестью своими копиями, расположенными вдоль ребер куба. Дипольная и квадрупольная составляющая в такой структуре точно равны нулю, а третья гармоника (октуполь) может иметь произвольное высокую амплитуду.
Во Вселенной, построенной из додекаэдров (см. Рис. 11), картина была бы несколько другой: каждый объект был бы окружен дюжиной своих копий, в такой структуре строго равна нулю амплитуда диполя, следующие две гармоники (квадруполь и октуполь) подавлены, а амплитуды остальных определяются распределением структур в начальном многограннике. Не правда ли, эта картина очень похожа на наблюдаемую? (см. Рис. 2.)
Очень легко представить и противоположную ситуацию, когда размеры видимой части Вселенной меньше начальной фигуры. В этом случае наблюдаемая нами картина не будет отличаться от того, что мы бы увидели в бесконечной Вселенной с простой топологией (это отличие может появиться на более поздних - в космологических масштабах - временах).
На самом деле все более сложно. Когда мы наблюдаем другие галактики, то мы смотрим не только в даль, но и в прошлое. Это связано с конечность скорости света. Если бы размер нашей Вселенной составлял несколько мегапарсек, свет от копий нашей Галактики доходил бы к нам за несколько миллионов лет, за это время галактика изменяется не слишком сильно, и мы смогли бы "узнать себя" в этих "отражения", а может быть даже попытались отыскать в них Солнечную систему. Если увеличить размеры начального мира до сотен тысяч световых лет подобное опознание становится затруднительным, а узнать Млечный Путь за 2-3 миллиарда лет до нашей эры мы бы просто не смогли. Однако, все поиски периодической структуры с размерами от 1000 мегапарсек и меньше, которые проводились последние 10-20 лет, не дали положительного результата. Это означает, что если наша Вселенная и имеет ограниченный объем, то его размеры очень велики, если мы и видим самих себя, то в настолько далеком прошлом, что какое-либо отождествление с современными объектами становится практически невозможным.
Космология
Какие предсказания дает додекаэдральная модель Вселенной и как они соотносятся с наблюдениями?
В данной модели пространство должно обладать положительной кривизной
(быть замкнутым), причем обладать строго определенным значением
отношения средней плотности к критической
![]() (это значение - математическая
константа, которую можно вычислить с любым числом знаков после
запятой). И это значение попадает внутрь допустимого диапазона! Данные
WMAP дают
(это значение - математическая
константа, которую можно вычислить с любым числом знаков после
запятой). И это значение попадает внутрь допустимого диапазона! Данные
WMAP дают
![]() .
.
[Более того, если рассчитать ожидаемый спектр возмущений не для
плоской модели с ![]() , как показано на Рис. 2, а для
, как показано на Рис. 2, а для ![]() , то
окажется, что и октуполь, и диполь гораздо лучше согласуются с
наблюдениями!]
, то
окажется, что и октуполь, и диполь гораздо лучше согласуются с
наблюдениями!]
Как устроена такая Вселенная?
Для космологической модели с ![]() радиус горизонта
будет составлять 38% от радиуса кривизны Вселенной (R), а
границы додекаэдра будут лежать в интервале от 31% R
(центры граней) до 39%R (вершины) от его центра. Объем
такого многогранника будет составлять 83% от объема сферы горизонта.
Отношение размеров додекаэдра к радиусу кривизны остается постоянным,
поскольку при расширении Вселенной эти величины изменяются
пропорционально друг другу. Горизонт Вселенной ведет себя по-другому.
Его поведение зависит от закона расширения, более подробно это описано
в статье С.Попова (и ссылках приведенных в
ней).
радиус горизонта
будет составлять 38% от радиуса кривизны Вселенной (R), а
границы додекаэдра будут лежать в интервале от 31% R
(центры граней) до 39%R (вершины) от его центра. Объем
такого многогранника будет составлять 83% от объема сферы горизонта.
Отношение размеров додекаэдра к радиусу кривизны остается постоянным,
поскольку при расширении Вселенной эти величины изменяются
пропорционально друг другу. Горизонт Вселенной ведет себя по-другому.
Его поведение зависит от закона расширения, более подробно это описано
в статье С.Попова (и ссылках приведенных в
ней).
Пятна на небе
Сложная топология нашей Вселенной будет проявляться в наблюдения только в том случае, если размеры горизонта превосходят размеры исходного многогранника и в доступную нам область Вселенной хотя бы частично попадают участки его копий. Если же исходная фигура превосходит по размерам горизонт, но наблюдаемая картина не будет отличаться от вида бесконечной Вселенной. Схематически данное утверждение показано на Рис. 12.
|
|
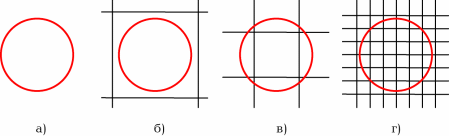
Рис. 12.
Возможные соотношения размеров горизонта (красная окружность) и
исходных многогранников: а) бесконечная Вселенная, б) горизонт меньше
исходного многогранника, в) горизонт слегка больше исходного многогранника,
г) горизонт охватывает много копий исходного многогранника.
В случаях а) и б) различий наблюдаться не будет. |
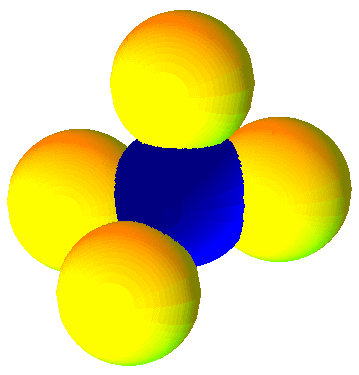
Для указанного выше размера горизонта (0.38R) наличие копий Вселенной будет проявляться в виде шести пар расположенных в противоположных направлениях на небесной сфере кругов диаметром 70o. Они образуются при пересечении сферы последнего рассеяния с гранями додекаэдра. Сфера последнего рассеяния (граница рекомбинации) по данным WMAP расположена на среднем красном смещении z=1089$\pm$1, т.е. слегка меньше горизонта. Температура реликтового излучения в каждом из кругов такой пары будет одинаковым образом отличаться от среднего ее значения, т.к. регистрируемое от кругов излучение испускается областями Вселенной, заполненных одним и тем же веществом (см. Рис. 13).
|
| Рис. 13. Пересекающиеся сферы последнего рассеяния для основного многогранника (показана синим цветом) и для некоторых его копий (желтым). |
Теоретические аспекты
То, что наша Вселенная может оказаться замкнутой, ставит определенные вопросы перед инфляционным сценарием, который сегодня успешно объясняет большинство свойств окружающей нас Вселенной. Полной ясности в этой проблеме (инфляция в замкнутой Вселенной) пока нет, но, кажется, космологи готовы к ее решению.
Заключение
Как подтвердить или опровергнуть модель, описанную в данной статье? Она предсказывает два следствия, которые допускают экспериментальную проверку, причем в ближайшее время:
- Вселенная должна быть замкнутой с
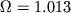 ;
;
- На небе должны наблюдаться 6 пар кругов диаметром 70o (центры которых соответствуют серединам граней правильного додекаэдра) распределение возмущений реликтового излучения в которых должно попарно кореллировать друг с другом.
И, конечно, остается возможность, что для приведенных в начале данной статьи фактов найдутся совсем другие объяснения. (Этого вполне можно ожидать, так как указаний в пользу именно такой топологически сложной модели Вселенной очень мало. Пока ими являются только низкие амплитуды двух первых гармоник спектра мощности реликтового излучения. Этого достаточно, чтобы начать обсуждать данную модель, но чтобы убедить научную общественность в ее "серьезности" нужны дополнительные аргументы.)
|
Публикации с ключевыми словами:
топология Вселенной - структура Вселенной - топология
Публикации со словами: топология Вселенной - структура Вселенной - топология | |
См. также:
Все публикации на ту же тему >> | |