Астронет > Чандрасекара предел

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

На сайте

Астрометрия

Астрономические инструменты

Астрономическое образование

Астрофизика

История астрономии

Космонавтика, исследование космоса

Любительская астрономия

Планеты и Солнечная система

Солнце

Чандрасекара предел

верхний предел массы ${\mathfrak M}_Ч$ холодного невращающегося белого карлика. Установлен С. Чандрасекаром (США) в 1931 г. Давление p внутри белого карлика (Б.к.) определяется электронным вырожденным газом и зависит только от плотности вещества $\rho$ . С увеличением $\rho$ электронный газ становится релятивистским, и эта зависимость асимптотически приближается к закону
$p=K\rho^{4/3}$ , (1)
где
$K={1\over 8} \left({3\over {\pi}} \right)^{1/3} {hc\over {(m_u\mu_e)^{4/3}}} \approx {1,244\cdot 10^{15}\over {\mu_e^{4/3}}} \left[ {см^3\over {с^2\cdot г^{1/3}}} \right]$ . (2)

Здесь m_u атомная единица массы, $\mu_e$ - молекулярная масса, приходящаяся на один электрон [число электронов в ед. объема равно $\rho/(m_u\mu_e)$ ]. Чем больше масса ${\mathfrak M}$ Б.к., тем точнее выполняется соотношение (1) и тем лучше строение Б.к. соответствует модели политропного шара. Теория политропных газовых шаров - гидростатически равновесных сферически-симметричных конфигураций, внутри к-рых $p\sim\rho^{1+{1\over n}}$ [случаю (1) соответствует n=3], - была развита в конце 19 - начале 20 вв. Дж. Лейном (США), А. Риттером (Германия) и Р. Эмденом (Швейцария). Согласно этой теории, в случае n=3 имеется однозначная связь между постоянной K и массой ${\mathfrak M}$ политропного шара:
$K=0,3639\cdot G{\mathfrak M}^{2/3}$ , (3)
где 0,3639 - коэффициент, определяемый условием гидростатич. равновесияю Подставляя значение K из (2) в (3), получаем предельную массу ${\mathfrak M}_Ч$ Б.к.
${\mathfrak M}_Ч={0,1967\over {(m_u\mu_e)^2}} \left( {hc\over G} \right)^{3/2} = {5,83\over {\mu_e^2}} {\mathfrak M}_\odot$ . (4)
Когда масса ${\mathfrak M}$ Б.к. приближается к ${\mathfrak M}_Ч$ снизу, плотность вещества внутри Б.к. неограниченно возрастает и связь между давлением и плотностью все точнее описывается соотношением (1). При этом радиус Б.к. стремится к нулю. При ${\mathfrak M}>{\mathfrak M}_Ч$ гидростатич. равновесие Б.к. вообще невозможно, поскольку градиент давления недостаточен для компенсации силы тяжести. В табл. для различных веществ приведены округленные значения $\mu_e$ и соответствующие ${\mathfrak M}_Ч$ :

¹H ⁴He, ¹²C, ¹⁴N, ¹⁶O, ²⁰Ne, ²⁴Mg, ²⁸Si, ⁴⁰Ca,... -
в чистом виде или смешанные
в любой пропорции ⁵²Cr ⁵⁶Fe ⁵⁹Co ⁵⁸Ni

$\mu_e$ 1,01 2,00 2,16 2,15 2,18 2,07

${{\mathfrak M}_Ч\over{{\mathfrak M}_\odot}}$ 5,73 1,46 1,24 1,26 1,22 1,36

При достаточно больших плотностях на структуру реальных Б.к. начинают заметно влиять процессы нейтронизации вещества и эффекты общей теории относительности. В результате макс. масса ${\mathfrak M}_{макс}$ Б.к. оказывается несколько меньше ${\mathfrak M}_Ч$ и ей соответствует уже не бесконечная, а конечная величина центральной плотности $\rho_с$ (рис.). Так, для углеродных Б.к. с учетом этих факторов ${\mathfrak M}_{макс}\approx 1,36 {\mathfrak M}_\odot$ и $\rho_{макс}\approx 5\cdot 10^{10}$ г/см³, чему соответствует минимальный радиус Б.к. ~ 10⁸ см, т.е. 1 тыс. км.

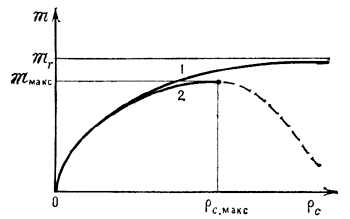
Качественный вид зависимости массы белых карликов
от их центральной плотности.
1 - идеальные белые карлики, для к-рых $\rho_c\to\infty$
при ${\mathfrak M}\to {\mathfrak M}_Ч$ ;
2 - реальные белые карлики: максимальной массе ${\mathfrak M}_{макс}$
соответствует конечная
центральная плотность $\rho_{c,макс}$ .
Штриховой отрезок кривой соответствет неустойчивым конфигурациям.

Достаточно горячие Б.к., электронный газ внутри к-рых вырожден не полностью, а также холодные, но быстро вращающиеся Б.к. могут иметь массы, превышающие ${\mathfrak M}_Ч$ . Со временем по мере охлаждения и (или) потери момента количества движения гидростатич. равновесие таких массивных Б.к. неминуемо нарушается и они переходят в состояние гравитационного коллапса , в результате чего возникает нейтронная звезда.

Ч.п. играет фундаментальную роль в теории строения и эволюции звезд. Внутри массивных звезд на определенных стадиях эволюции могут образовываться частично вырожденные центральные ядра, состоящие из C, O, Ne, Si, Fe. Характер последующих, заключительных стадий эволюции таких звезд, а также их конечная судьба критически зависят от того, насколько и в какую сторону отличаются массы их ядер от ${\mathfrak M}_Ч$ .

(Д.К. Надежин)

Д. К. Надежин, "Физика Космоса", 1986
Глоссарий Astronet.ru

А | Б | В | Г | Д | З | И | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Э | Я

Публикации с ключевыми словами: предел Чандрасекара - Чандрасекаровская масса Публикации со словами: предел Чандрасекара - Чандрасекаровская масса
См. также: Рассвет перед взрывом новой звезды Белые карлики Субрахманьян Чандрасекар (1910-1995 гг.) Предел, Чандрасекара

Обсудить эту публикацию

Версия для печати

	¹H	⁴He, ¹²C, ¹⁴N, ¹⁶O, ²⁰Ne, ²⁴Mg, ²⁸Si, ⁴⁰Ca,... - в чистом виде или смешанные в любой пропорции	⁵²Cr	⁵⁶Fe	⁵⁹Co	⁵⁸Ni
$\mu_e$	1,01	2,00	2,16	2,15	2,18	2,07
${{\mathfrak M}_Ч\over{{\mathfrak M}_\odot}}$	5,73	1,46	1,24	1,26	1,22	1,36