Элементы орбиты
- величины, характеризующие орбиту небесного тела, а также положения тела на орбите.
|
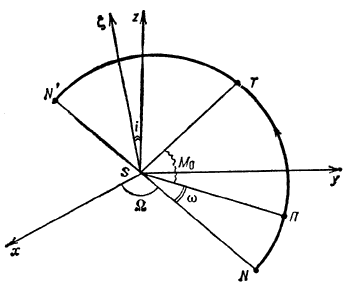
| Рис. 1 |
Орбита небесного тела, движущегося в поле тяготения др. тела, представляет собой кривую второго порядка (конич. сечение), в одном из фокусов к-рой находится центр масс двух тел (притягивающий центр). Данное определение относится к случаю, когда взаимодействующие тела сферически-симметричны или же находятся на столь большом расстоянии, что отклонение их формы от сферической не сказывается существенно на силе взаимодействия.
Точка орбиты тела, ближайшая к притягивающему центру, наз. перицентром, а наиболее удаленная - апоцентром. Если притягивающим центром явл. Земля, то эти точки наз. перигеем и апогеем; для Солнца - перигелием и афелием, для произвольной звезды - периастром и апоастром. Прямая, соединяющая апоцентр и перицентр, носит название линии апсид.
Элементы, характеризующие положение плоскости орбиты и ориентацию орбиты в жтой плоскости, вводятся след. образом.
На рис. 1 Sxy - осн. координатная плоскость. За осн. координатную плоскость в разных задачах выбирают различные плоскости: в звездной астрономии - это плоскость Галактики, в теории движения ИСЗ - это плоскость земного экватора.
Ось Sx направлена в основную точку, за к-рую для
орбит тел в Солнечной системе чаще всего принимают точку весеннего равноденствия
![]() (одну из точек пересечения экватора с эклиптикой). Плоскость NПN' - плоскость
орбиты небесного тела, П - перицентр орбиты,
(одну из точек пересечения экватора с эклиптикой). Плоскость NПN' - плоскость
орбиты небесного тела, П - перицентр орбиты, ![]() - полюс орбиты
(он находится на прямой, проходящей через тяготеющий центр и перпендикулярной к плоскости
орбиты), T - положение небесного тела на орбите.
- полюс орбиты
(он находится на прямой, проходящей через тяготеющий центр и перпендикулярной к плоскости
орбиты), T - положение небесного тела на орбите.
Прямая NSN', по к-рой плоскость орбиты NПN' пересекается с осн. координатной
плоскостью Sxy, наз. линией узлов. Полупрямая SN,
к-рую небесное тело пересекает, переходя из области z <0 в область z
>0, показывает положит. направление линии узлов. Если движение небесного тела происодит
против часовой стрелки для наблюдателя, находящегося в полюсе орбиты ![]() ,
то точка N наз. восходящим узлом орбиты, а N' - нисходящим узлом. Угол
,
то точка N наз. восходящим узлом орбиты, а N' - нисходящим узлом. Угол
![]() между осью Sx и полупрямой SN
наз. долготой восходящего узла. Этот угол отсчитывается от оси Sx
в сторону оси Sy от 0 до 360o.
Угол i между плоскостью орбиты и плоскостью Sxy
наз. наклоном орбиты. Наклон может иметь все значения от 0 до 180o.
Если
между осью Sx и полупрямой SN
наз. долготой восходящего узла. Этот угол отсчитывается от оси Sx
в сторону оси Sy от 0 до 360o.
Угол i между плоскостью орбиты и плоскостью Sxy
наз. наклоном орбиты. Наклон может иметь все значения от 0 до 180o.
Если ![]() , то движение наз. прямым, если же
, то движение наз. прямым, если же ![]() , то обратным. Угловое расстояние
, то обратным. Угловое расстояние ![]() линии
апсид SП от линии узлов SN наз. расстоянием перицентра от узла или
аргументом
перицентра. Угол
линии
апсид SП от линии узлов SN наз. расстоянием перицентра от узла или
аргументом
перицентра. Угол ![]() отсчитывается в направлении движения тела от
0 до 360o. Положение линии апсид иногда определяют относительно
направления Sx. Для этого вводят угол
отсчитывается в направлении движения тела от
0 до 360o. Положение линии апсид иногда определяют относительно
направления Sx. Для этого вводят угол ![]() - долготу перицентра. Угол
- долготу перицентра. Угол ![]() отсчитывается от направления Sx
в плоскости xSy до линии узолов SN и далее
в плоскости орбиты до линии апсид SП, иначе
отсчитывается от направления Sx
в плоскости xSy до линии узолов SN и далее
в плоскости орбиты до линии апсид SП, иначе ![]() .
.
|
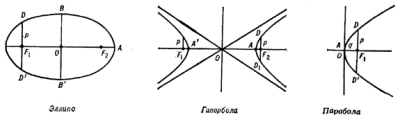
| Рис. 2 |
Величины ![]() составляют первую группу элементов орбиты,
первые для из них характеризуют положение плоскости орбиты, а третий - ориентацию
орбиты
в этой плоскости.
составляют первую группу элементов орбиты,
первые для из них характеризуют положение плоскости орбиты, а третий - ориентацию
орбиты
в этой плоскости.
Размер орбиты и ее форму характеризуют элементы p и e - параметр и
эксцетреситет (рис. 2). Эксцетреситетом орбиты e наз. отношение расстояния
между фокусами
F1F2=2c этой орбиты к
расстоянию между ее вершинами A и A'. Расстояние между ее вершинами
обозначают
2a, а величину a наз. большой полуосью орбиты, так что e=c/a.
Для параболы c=a, поэтому e=1. Для эллипса e <1, для гиперболы
e
>1. Половина фокальной хорды DD' орбиты, перпендикулярной к ее оси, носит
название фокального параметра и обозначается буквой p. Вместо двух элементов
p
и e для параболы используют один элемент q=p/2 - перигелийное расстояние
(на рис. 2 отрезок AF1). Движение по круговой орбите
явл. частным случаем движения по эллипсу (e=0). Эксцетреситетом орбиты e
иногда заменяют углом эксцетреситета ![]() , определяемым ф-лой
, определяемым ф-лой ![]() .
Положение небесного тела на орбите в нек-рый начальный момент времени t0
определяется его угловым расстоянием от линии апсид. Этот угол обозначается
через M0 и наз. средней аномалией в эпоху. Часто
в качетве элемента выбирают момент времени
.
Положение небесного тела на орбите в нек-рый начальный момент времени t0
определяется его угловым расстоянием от линии апсид. Этот угол обозначается
через M0 и наз. средней аномалией в эпоху. Часто
в качетве элемента выбирают момент времени ![]() прохождения небесного
тела через
перицентр орбиты. Элементы M0 и
прохождения небесного
тела через
перицентр орбиты. Элементы M0 и ![]() связаны между собой соотношением
связаны между собой соотношением ![]() , где n - среднее
движение
небесного тела. Элемент n иногда употребляют вместо элемента a.
, где n - среднее
движение
небесного тела. Элемент n иногда употребляют вместо элемента a.
Элементы ![]() наз. кеплеровскими элементами.
Они определяют орбиту независимо от того, явл. ли она эллиптической, гиперболической
или
параболической.
наз. кеплеровскими элементами.
Они определяют орбиту независимо от того, явл. ли она эллиптической, гиперболической
или
параболической.
Скорость кругового движения (первая космическая скорость) определяется ф-лой ![]() ,
где
,
где ![]() - произведение гравитац. постоянной на сумму
масс притягивающих тел, r - расстояние между их центрами масс. При vK
< v < vП движение происходит по эллипсу.
При
- произведение гравитац. постоянной на сумму
масс притягивающих тел, r - расстояние между их центрами масс. При vK
< v < vП движение происходит по эллипсу.
При ![]() эллипс разрывается и тело движется по параболической
траектории. Скорость vП наз. скоростью отрыва от
притягивающего центра или второй космической скоростью. При v > vП
небесное тело движется по гиперболе.
эллипс разрывается и тело движется по параболической
траектории. Скорость vП наз. скоростью отрыва от
притягивающего центра или второй космической скоростью. При v > vП
небесное тело движется по гиперболе.
(С.Н. Вашковьяк)
С. Н. Вашковьяк, "Физика Космоса", 1986
Глоссарий Astronet.ru
|
Публикации с ключевыми словами:
элементы орбиты
Публикации со словами: элементы орбиты |

|
|
См. также:
| |