Астронет > Уровни энергии (атомные, молекулярные, ядерные)

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

На сайте

Астрометрия

Астрономические инструменты

Астрономическое образование

Астрофизика

История астрономии

Космонавтика, исследование космоса

Любительская астрономия

Планеты и Солнечная система

Солнце

Уровни энергии (атомные, молекулярные, ядерные)

1. Характеристики состояния квантовой системы
2. Энергетические уров атомов
3. Энергетические уровни молекул
4. Энергетические уровни ядер

1. Характеристики состояния квантовой системы

В основе объяснения св-в атомов, молекул и атомных ядер, т.е. явлений, происходящих в элементах объема с линейными масштабами 10^-6-10^-13 см, лежит квантовая механика. Согласно квантовой механике, всякая квантовая система (т.е. система микрочастиц, к-рая подчиняется квантовым законам) характеризуется определенным набором состояний. В общем случае этот набор состояний может быть как дискретным (дискретный спектр состояний), так и непрерывным (непрерывный спектр состояний). Характеристиками состояния изолированной системы явл. внутренняя энергия системы (всюду дальше просто энергия), полный момент количества движения (МКД) и четность.

Энергия системы.
Квантовая система, находясь в различных состояниях, обладает, вообще говоря, различной энергией. Энергия связанной системы может принимать любые значения. Этот набор возможных значений энергии наз. дискретным энергетическим спкетром, а об энергии говорят, что она квантуется. Примером может служить энергетич. спектр атома (см. ниже). Несвязанная система взаимодействующих частиц обладает непрерывным энергетическим спектром, а энергия может принимать произвольные значения. Примером такой системы явл. свободный электрон (Э) в кулоновском поле атомного ядра. Непрерывный энергетический спектр можно представить как набор бесконечно большого числа дискретных состояний, между к-рыми энергетич. зазоры бесконечно малы.

Состояние, к-рому соответствует наименьшая энергия, возможная для данной системы, наз. основным: все остальные состояния наз. возбужденными. Часто бывает удобным пользоваться условной шкалой энергии, в к-рой энергия осн. состояния считается началом отсчета, т.е. полагается равной нулю (в этой условной шкале всюду в дальнейшем энергия обозначается буквой E). Если система, находясь в состоянии n (причем индекс n=1 присваивается осн. состоянию), обладает энергией E_n, то говорят, что система находится на энергетическом уровне E_n. Число n, нумерующее У.э., наз. квантовым числом. В общем случае каждый У.э. может характеризоваться не одним квантовым числом, а их совокупностью; тогда индекс n означает совокупность этих квантовых чисел.

Если состояниям n₁, n₂, n₃,..., n_k соответствует одна и та же энергия, т.е. один У.э., то этот уровень называется вырожденным, а число k - кратностью вырождения.

При любых превращениях замкнутой системы (а также системы в постоянном внеш. поле) ее полная энергия энергия сохраняется неизменной. Поэтому энергия относится к т.н. сохраняющимся величинам. Закон сохранения энергии следует из однородности времени.

Полный момент количества движения.
Эта величина явл. векторной и получается сложением МКД всех частиц, входящих в систему. Каждая частица обладает как собств. МКД - спином, так и орбитальным моментом, обусловленным движением частицы относительно общего центра масс системы. Квантование МКД приводит к тому, что его абс. величина J принимает строго определенные значения: $J=\hbar\sqrt{j(j+1)}$ , где j - квантовое число, к-рое может принимать неотрицательные целые и полуцелые значения (квантовое число орбитального МКД всегда целое). Проекция МКД на к.-л. ось наз. магн. квантовым числом $m_j$ и может принимать 2j+1 значений: m_j=j, j-1,...,-j. Если к.-л. момент J явл. суммой двух др. моментов ${\bf J}={\bf J}_1+{\bf J}_2$ , то, согласно правилам сложения моментов в квантовой механике, квантовое число j может принимать следующие значения: j=|j₁-j₂|, |j₁-j₂-1|, ...., |j₁+j₂-1|, j₁+j₂, а $m_j=m_{j_1}+m_{j_2}$ . Аналогично производится суммирвоание большего числа моментов. Принято для краткости говорить о МКД системы j, подразумевая при этом момент, абс. величина к-рого есть $\hbar\sqrt{j(j+1)}$ ; о магн. квантовом числе говорят просто как о проекции момента.

При различных превращениях системы, находящейся в центрально-симметричном поле, полный МКД сохраняется, т.е., как и энергия, он относится к сохраняющимся величинам. Закон сохранения МКД следует из изотропии пространства. В аксиально-симметричном поле сохраняется лишь проекция полного МКД на ось симметрии.

Четность состояния.
В квантовой механике состояния системы описываются т.н. волновыми ф-циями. Четность характеризует изменение волновой ф-ции системы при операции пространственной инверсии, т.е. замене знаков координат всех частиц. При такой операции энергия не изменяется, тогда как волновая ф-ция может либо остаться неизменной (четное состояние), либо изменить свой знак на противоположный (нечетное состояние). Четность P принимает два значения, соответственно $P=\pm 1$ . Если в системе действуют ядерные или эл.-магн. силы, четность сохраняется в атомных, молекулярных и ядерных превращениях, т.е. эта величина также относится к сохраняющимся величинам. Закон сохранения четности явл. следствием симметрии пространства по отношению к зеркальным отражениям и нарушается в тех процессах, в к-рых участвуют слабые взаимодействия.

Квантовые переходы
- переходы системы из одного квантового состояния в другое. Такие переходы могут приводить как к изменению энергетич. состояния системы, так и к ее качеств. изменения. Это связанно-связанные, свободно-связанные, свободно-свободные переходы (см. Взаимодействие излучения с веществом), напр., возбуждение, деактивация, ионизация, диссоциация, рекомбинация. Это также хим. и ядерные реакции. Переходы могут происходить под действием излучения - излучательные (или радиацианные) переходы или при столкновении данной системы с к.-л. др. системой или частицей - безызлучательные переходы. Важной характеристикой квантового перехода явл. его вероятность в ед. времени, показывающая, как часто будет происходить данный переход. Эта величина измеряется в с^-1. Вероятности радиац. переходов между уровнями m и n (m>n) с излучением или поглощением фотона, энергия к-рого равна $h\nu_{mn}=E_m-E_n$ , определяются коэфф. Эйнштейна A_mn, B_mn и B_nm. Переход с уровня m на уровень n может происходить спонтанно. Вероятность излучения фотона B_mn в этом случае равна A_mn. Переходы типа $m\rightleftharpoons n$ под действием излучения (индуцированные переходы) характеризуются вероятностями излучения фотона $R_{mn}=B_{nm} \rho_\nu$ и поглощения фотона $R_{nm}=B_{nm} \rho_\nu$ , где $\rho_\nu$ - плотность энергии излучения с частотой $\nu$ .

Возможность осуществления квантового перехода с данного У.э. на к.-л. другой У.э. означает, что характерное ср. время $\Delta t$ , в течение к-рого система может находится на этом У.э., конечно. Оно определяется как величина, обратная суммарной вероятности распада данного уровня, т.е. сумме вероятностей всех возможных переходов с рассматриваемого уровня на все другие. Для радиац. переходов суммарная вероятность есть $R_m=\sum\limits_i R_{mi}$ , а $\Delta t=R_m^{-1}$ . Конечность времени $\Delta t$ , согласно соотношению неопределенностей $\Delta E \cdot \Delta t \ge \hbar$ , означает, что энергия уровня не может быть определена абсолютно точно, т.е. У.э. обладает нек-рой шириной. Поэтому излучение или поглощение фотонов при квантовом переходе $m\to n$ происходит не на строго определенной частоте $\nu_{mn}$ , а внутри нек-рого частотного интервала, лежащего в окрестности значения $\nu_{mn}$ . Рапределение интенсивности внутри этого интервала задается профилем спектральной линии $\varphi(\nu)$ , определяющим вероятность того, что частота фотона, испущенного или поглощенного при данном переходе, равна $\nu$ :
$\varphi(\nu)={\Delta \nu\over {\pi}}\cdot {1 \over {(\nu-\nu_{mn})^2+(\Delta \nu)^2}}$ (1)
где $\Delta \nu=(R_m-R_n)/4\pi$ - полуширина профиля линии. Если уширение У.э. и спектральных линий вызвано только спонтанными переходами, то такое уширение наз. естественным. Если в уширении определенную роль играют столкновения системы с др. частицами, то уширение имеет комбинирвоанный характер и величина $\Delta \nu$ должна быть заменена суммой $\Delta \nu + (\Delta \nu)_C$ , где $(\Delta \nu)_C$ вычисляется подобно $\Delta \nu$ , но радиац. вероятности переходов должны быть заменены столкновительными вероятностями.

Переходы в квантовых системах подчиняются определенным правилам отбора, т.е. правилам, устанавливающим, как могут меняться при переходе квантовые числа, характеризующие состояние системы (МКД, четность и т.п.). Наиболее просто правила отбора формулируются для радиац. переходов. В этом случае они определяются св-вами начального и конечного состояний, а также квантовыми характеристиками излучаемого или поглощаемого фотона, в частности его МКД и четностью. Наибольшей вероятностью обладают т.н. электрические дипольные переходы. Эти переходы осуществляются между уровнями противоположной четности, полные МКД к-рых отличаются на величину $\Delta J =0, \pm 1$ (переход $J=0 \to 0$ невозможен). В рамках сложившейся терминологии эти переходы наз. разрешенными. Все остальные типы переходов (магнитный дипольный, электрический квадрупольный и т.п.) наз. запрещенными. Смысл этого термина состоит лишь в том, что их вероятности оказываются много меньше вероятностей дипольных электрических переходов. Однако они не явл. запрещенными абсолютно.

2. Энергетические уровни атомов

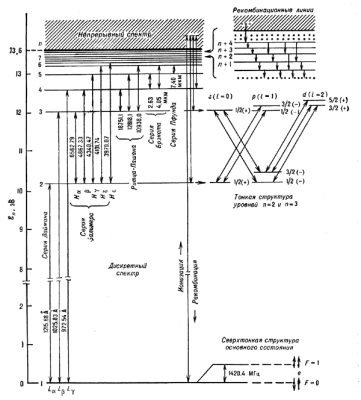
Атом водорода.
Простейшим атомом (А) явл. А водорода, состоящий из протона и Э, связанных гл. обр. электростатическим кулоновским взаимодействием. Качественно подобен А водорода водородоподобный ион, т.е. система, состоящая из ядра с зарядом Z и одного Э. Схема У.э. А водорода показана на рис. 1. Энергия уровней в нерелятивистском приближении дается выражением:
$E_n=R_H \left( 1- {1 \over {n^2}} \right)$ , (2)
где $R_H=13,6058$ эВ - Ридберга постоянная для А водорода, величина n наз. главным квантовым числом и может принимать значения n=1, 2, 3, ...., $\infty$ . У.э., соответствующие различным n, показаны в левой части рисунка; при увеличении n они сгущаются к границе ионизации 13,6 эВ. Переходы между У.э. с различными значениями n приводят к образованию спкетра, состоящего из отчетливо выраженных спектральных серий (для серий Брэкета и Пфунда длины волн на рис. даны в микрометрах, для остальных - в ангстремах). Наблюдение и излучение этих линий играет важную роль в исследовании атмосфер звезд. В результате существенного улучшения чувствительности астрономич. приемников ИК-излучения удалось наблюдать линии, принадлежащие сериям Брэкета и Пфунда, к-рые образуются в компактных зонах HII, окружающих очень молодые звезды.

Рис. 1. Схема энергетических уровней атома водорода.
Длины волн даны в $\AA$ . Для серий Брэкета и Пфунда в мкм.

На рис. 1 показаны также переходы между уровнями, лежащими в дискретном и непрерывном спектре: свободно-связанные переходы - рекомбинация и обратные связанно-свободные переходы - ионизация.

Рекомбинация атомов на У.э. с большмим значениями n и последующие каскадные переходы на нижележащие уровни приводят к образованию линий, получивших название рекомбинационных (см. Рекомбинационные радиолинии). Нек-рые из таких переходов показаны в верхней правой части рис. 1.

Электрон в А в общем случае обладает орбитальным МКД l, к-рый может принимать целочисленные значения в интервале $0 \le l \le n-1$ . В атомной спектроскопии принято обозначать состояния, соответствующие различным значениям l=0, 1, 2, ..., буквами латинского алфавита s, p, d, f, g (и далее в порядке букв латинского алфавита). Например, состояние n=1, l=0 обозначается как 1s, состояние n=3, l=2 - 3d. Так, к У.э. n=1 относится одно состояние 1s, к У.э. n=2 - состояния 2s, 2p, к У.э. n=3 - состояния 3s, 3p, 3d, и т.д.

Согласно (2), в нерелятивистском приближении энергия уровня с квантовым числом n не зависит от l и m_l (m_l - проекция орбитального МКД на к.-л. ось). Т.о., в этом приближении уровень n оказывается вырожденным. Кратность этого вырождения есть n². Независимость энергии от m_l легко объясняется тем, что в поле, обладающим сферич. симметрией (таково кулоновское поле ядра), все направления в пространстве равноправны, и поэтому энергия не может зависеть от ориентации МКД в пространстве. Что касается независимости энергии от l, то она связана только со спецификой кулоновского взаимодействия между ядром и Э. Вырождение по l снимается, когда при расчете энергии атомного У.э. учитываются такие релятивистские поправки, как зависимость массы Э от скорости (см. Релятивистские частицы) и спин-орбитальное взаимодействие, т.е. взаимодействие, зависящее от величин и взаимной ориентации орбитального и спинового МКД Э. Учет этих поправок дает следующую ф-лу для энергии уровня:
$E_{nlj}=R_H\left(1- {1\over {n^2}} \left[1- {\alpha^2 \over n} \left( {3\over {4n}} - {1\over {j+1/2}}\right) \right] \right)$ , (3)
где $\alpha=e^2/\hbar c$ =1/137 - постоянная тонкой структуры, j - полный МКД, слагающийся из орбитального и спинового МКД. Согласно правилам сложения МКД, j может принимать два значения: $j=l\pm 1/2$ . Т.о., каждое состояние с $l \ne 0$ расщепляется на два уровня с различными энергиями. Эти расщепления много меньше, чем расстояния между У.э. с различными значениями n, и наз. тонкими расщеплениями (тонкая структура). Тонкая структура У.э. с n=2 и n=3 в А водорода показана на рис. 1. Справа от каждого У.э. указаны значения j и четность уровня, а стрелками показаны переходы, ответственные за линию H $_\alpha$ (самая длинноволновая линия в серии Бальмера). Аналогичная структура имеется у всех уровней n >0, l >0. Величина тонкого расщепления убывает с ростом n как 1/n³. Поэтому оно особенно важно для нижних состояний.

Расщепление еще меньшей величины (сверхтонкое расщепление) обязано взаимодействию магн. моментов ядра и Э. Это расщепление показано на рис. 1 для осн. состояния А водорода. Магн. моменты Э и ядра (в данном случае протона) пропорциональны их спинам. Поскольку спин протона I=1/2, то полный МКД А в осн. состоянии (при учете ядерного спина он обычно обозначается буквой F) может принимать два значения: F=1 (спины e и p параллельны) и F=0 (спины e и p антипараллельны). Энергии этих сверхтонких подуровней различны, а переходы между ними приводят к образованию радиолинии водорода 21 см.

Многоэлектронные атомы.
В многоэлектронных атомах помимо кулоновского взаимодействия каждого Э с ядром имеются также взаимодействия Э друг с другом и обменное взаимодействие, связанное с неразличимостью Э при их квантовомеханическом описании. Движение каждого из Э можно рассматривать происходящим в нек-ром усредненном поле, создаваемом ядром и всеми др. Э. Для приближенного описания можно использовать квантовые числа n и l, однако в данном случае вырождение по l отсутствует даже в нерелятивистском приближении. Тем не менее каждый У.э. с данными n и l еще остается вырожденным по проекции орбитального и спинового МКД. Кратность этого вырождения равна (2s+1)(2l+1)=2(2l+1), т.к. для электрона s=1/2. Согласно принципу Паули, в каждом из этих состояний может находится только по одному Э. Поэтому максимально возможное число состояний в А с данными n и l равно 2(2l+1) и эти состояния, называемые эквивалентными, образуют электронную оболочку. Электронная оболочка наз. замкнутой, если все возможные состояния в ней заполнены. Совокупность 2n² состояний с одним и тем же n, но разными l наз. электронным слоем (напр., K-слой, содержащий 2 Э при n=1, L-слой, содержащий 8 Э при n=2, M-слой, содержащий 18 Э при n=3). закономерностями в последовательном заполнении электронных оболочек объясняется периодичность изменения св-в элементов. Последовательность, в к-рой возрастают энергии Э с заданными n и l, следующая: 1s, 2s, 2p, 3s, 3p, 3d, ... и т.д. (здесь буквы лат. алфавита, как и ранее, относятся к значениям орбитального МКД l=0, 1, 2, ...). Совокупность всех атомных Э, находящихся в определенных энергетич. состояниях, наз. электронной конфигурацией А. Для ее описания указывают, каким образом при возрастании n Э рапределяются по оболочкам. Для этого перечисляют все электронные оболочки, в к-рых есть Э, а именно: указывают главное квантовое число n, лат. буквуЮ соответствующую значению орбитального МКД l, и (сверху справа от этой буквы) число Э в данной оболочке. Напр., конфигурация 1s² 2s² 2p² осн. состояния А углерода означает, что в первом электронном слое находится два s-электрона, во втором слое находится два Э в s-оболочке и два Э в p-оболочке.

Электронная конфигурация определяет энергию А лишь приближенно. Для дальнейшего уточнения этой величины необходимо знать, какой тип связи МКД Э реализуется в А. Опыт показывает, что в легких А, где релятивистские эффекты сравнительно малы, реализуется т.н. LS-тип связи (часто ее называют также нормальной или связью Рассела-Саундерса). В этом случае все орбитальные МКД Э складываются в орбитальный МКД L , а все электронные спины суммируются в момент S. Моменты L и S складываются в полный МКД электронной оболочки J. В тяжелых А, где релятивистские эффекты существенны (спин-орбитальное и спин-спиновое взаимодействия), реализуется т.н. jj-связь, а именно: орбитальный j и спиновой s МКД каждого Э складываются в полный МКД электронной оболочки А J. Следует отметить, что, вообще говоря, чистых типов связи в реальных А не бывает и указанные типы - это предельные случаи, с хорошей точностью реализуемые для легких (LS) и тяжелых (jj) А. В астрофизич. приложениях наибольший интерес представляет рассмотрение У.э. в А с LS-связью моментов в электронных оболочках. Поэтому она описана здесь более подробно (о jj-связи см. раздел 4 и лит. при статье).

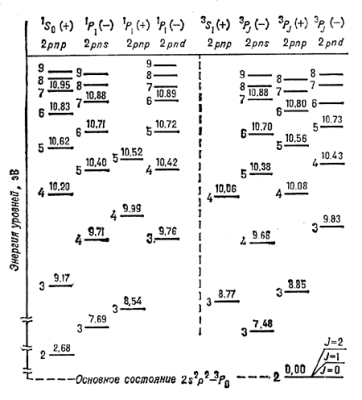
Рис. 2. Участок энергетического спектра
атома углерода. Числа, стоящие над чертой,
к-рая обозначает уровень, дают его энергию в эВ.
Главные квантовые числа n указаны слева от
обозначения уровней.

Если в электронной оболочке А реализуется LS-связь, то У.э., соответствующий данной электронной конфигурации, расщепляется на целый ряд уровней, характеризуемых значениями L и S, наз. спектральными термами. Для обозначения термов обычно используются заглавные буквы лат. алфавита. Значения L=0, 1, 2, ... соответствуют термы S, P, D, F, G и т.д. Вместо значения спина S указывают мультиплетность терма, равную 2S+1, к-рая ставится слева вверху у знака терма. Если мультиплетность равна 1, терм наз. синглетным, 2 - дублетным, 3 - триплетным и т.д. Эмпирически установленоЮ что наименьшей энергией обладает терм с наибольшим возможным для данной электронной конфигурации значением S и наибольшим (возможным при этом S) значением L (правило Хунда). Релятивистские эффекты, и прежде всего спин-орюитальное взаимодействие, приводят к расщеплению терма с данными L и S на ряд уровней, соответствующих различным возможным значениям J полного МКД ( $|L-S| \le J \le L+S$ ). Это расщепление наз. тонким или мультиплетным. Для характеристики состояния при наличии тонкой структуры наряду с электронной конфигурацией, термом и мультиплетностью указывают также значение полного МКД J, к-рое ставится справа внизу у обозначения терма. Напр., осн. состояние А углерода есть 1s² 2s² 2p² - ³P₀, т.е. электронная конфигурация осн. состояния А углерода есть 1s² 2s² 2p², полный орбитальный МКД L=1, полный спиновый МКД S=1, полный МКД электронной оболочки J=0. На рис. 2 приведен участок энергетич. спектра А углерода. В верхней части рис. термы, мультиплетности, значения полных моментов J, четности и электронные конфигурации. Все уровни разбиваются на две группы с различными мультиплетностями: синглеты (S=0) и триплеты (S=1). Радиац. переходы между этими двумя группами уровней (интеркомбинационные переходы) явл. запрещенными. Для терма ³P₀ показана тонкая структура.

В межзвездной среде наблюдается большое количество УФ- и оптич. линий, соответстсвующих различным переходам в многоэлектронных А и ионах. Ряд переходов из возбужденных состояний в нижние электронные слои (K-, L-слои) в тяжелых А приводит к излучению в рентг. области спектра.

Наличие тонкой структуры у многих А играет большую роль в астрофизич. явлениях. Напр., в А углерода и кислорода уровни тонкой структуры легко возбуждаются при столкновениях этих А с др. частицами в облаках межзвездного газа. Излучательная деактивация уровней тонкой структуры, сопровождающаяся излучением фотонов, способствует выводу тепловой энергии из газово-пылевых облаков. Этот процесс может оказаться особенно важным на начальном этапе звездообразования при уплотнении газовых конденсаций, в к-рых начинается гравитац. сжатие протозвезд. Переходы между уровнями тонкой структцры А и ионов кислорода, углерода, серы, аргона, неона и др. наблюдаются в межзвездной среде в ИК-диапазоне.

Как и в А водорода, в многоэлектронных А имеются сверхтонкие расщепления У.э. Переходы между уровнями сверхтонкой структуры попадают в радиодиапазон. Напр., длина волны такого перехода в А азота равна 11,5 м. Предпринимаются поиски этой линии в межзвездной среде.

Рекомбинация многоэлектронных А на У.э. с большими значениями n и последующие излучательные переходы между этими уровнями приводят к образованию рекомбинац. линий. Из-за того что массы ядер сложных А больше, чем масса ядра А водорода, рекомбинац. линии этих А слегка сдвинуты относительно соответстсвующих водородных линий в коротковолновую область спектра.

3. Энергетические уровни молекул

Основные типы движений в молекулах.
В общем случае в молекуле (М) имеется три типа движений: электронное, колебательное и вращательное. Движение каждого Э в М происходит в электрическом поле атомных ядер и в поле всех других Э. Так же как и в атомах в М электроны образуют вполне определенные конфигурации, а электронная энергия $E_{эл}$ квантуется. Состояние М, соответствующее определенному значению $E_{эл}$ , наз. электронным состоянием. В отличие от атомов, в М $E_{эл}$ в каждом электронном состоянии не явл. определенной постоянной величиной, но зависит от межъядерных расстояний (длин связи) и углов между ними (валентных углов). Эта функциональная зависимость наз. поверхностью потенциальной энергии (или кривой потенциальной энергии для двух атомной М). Поверхность потенциальной энергии, соответствующая связанному состоянию М, имеет минимум при некоторых значениях длин связи и валентных углов - эти значения наз. равновесными. Классификация электронных состояний многоатомных М проводится методами теории групп.

Наиболее простыми системами с точки зрения классификации энергетических состояний явл. линейные, или двухатомные М. В линейной М электрическое поле, действующее на Э, обладает аксиальной симметрией. Поэтому каждое электронное состояние характеризуется определенным значением проекции суммарного орбитального МКД всех Э на ось М. Эта величина обозначается $\Lambda$ . Различным значениям абс. величины $\Lambda$ соответствуют различные электронные состояния, или термы, к-рые обозначаются большими буквами греч. алфавита: $\Lambda=0 - \Sigma$ -состояние, $\Lambda=1 - \Pi$ -состояние, $\Lambda=2 - \Delta$ -состояние и т.д. Электронные состояния характеризуются также суммарным спином всех электронов S. Спин-орбитальное взаимодействие приводит к расщеплению электронного терма с данным S на 2S+1 близко лежащих У.э. (тонкая структура). Число 2S+1 наз. мультиплетностью электронного терма и ставится слева вверху у греч. буквы, указывающей значение $\Lambda$ , напр., $^2\Pi$ , $^3\Sigma$ . Опыт показывает, что осн. электронное состояние большинства М есть $^1\Sigma$ -состояние. Существует, однако, ряд М, в т.ч. такие межзвездные М как OH, NO, CH, осн. состояние к-рых характеризуется отличными от нуля значениями L или/и S.

При $\Lambda\ne 0$ возможны два состояния с одинаковой энергией, отличающиеся знаком проекции орбиального МКД на ось М ( $\pm\Lambda$ ). Т.о., все состояния с $\Lambda\ne 0$ двухкратно вырождены. $\Sigma$ -состояния не вырождены. Различают $\Sigma^+$ - и $\Sigma^-$ -состояния. Знаки $\pm$ обозначают четность состояния по отношению к операции отражения в плоскости, содержащей ось М. Если М обладает центром симметрии (напр., H₂, O₂, CO₂, H₂C₂), то появляется дополнит. квантовое число - четность по отношению к инверсии пространства. Четные состояния обозначают индексом $g (\Sigma_g, \Pi_g,...)$ , а нечетные - индеском $u (\Sigma_u, \Pi_u,...)$ .

Осн. св-ва кривых потенциальной энергии иллюстрируются рис. 3, где показаны такие кривые для трех электронных состояний молекулы H₂ - $^1\Sigma^+_g, ^3\Sigma^+_u, ^1\Sigma^+_u$ (для наглядности масштабы по осям энергии и межъядерных расстояний не выдержаны точно). Кривые для $^1\Sigma^+_g-, ^1\Sigma^+_u-$ состояний имеют минимумы при равновесных межъядерных расстояниях R=R_e и соответствуют связанным состояниям М. При $R\to \infty$ оба атома водорода свободны и E_эл равна сумме энергий обоих атомов. Величина $E_{\mbox{эл}}(\infty)$ наз. границей диссоциации. При сближении атомов образуется устойчивая М. Когда R < R_e, потенциальная энергия растет, т.к. начинает сказываться кулоновское отталкивание ядер. Разность энергий $D_c=E_{эл}(\infty)-E_{эл}(R_e)$ наз. энергией диссоциации. Кривая потенциальной энергии для состояния $^3\Sigma^+_u$ не имеет минимума, т.е. это состояние не явл. связанным. Сближающиеся атомы с таким набором квантовых чисел после столкновения расходятся, и М не образуется.

Колебания молекулы.
Из вида потенциальной кривой для связанного состояния М ясно, что при уменьшении или увеличении межъядерного расстояния относительно равновесного появляется сила, стремящаяся вернуть ядра в положение равновесия, R=R_e. Эта сила приводит к возникновению колебательного движения ядер.

В многоатомных М колебательные движения ядер заключаются в периодическом изменении длин связей и валентных углов относительно их равновесных значений. Колебательное движение квантуется, что приводит к возникновению дискретного колебательного энергетического спектра. Каждый колебательный У.э. двухатомной М (число колебательных степеней свободы i=1 - одномерное движение) характеризуется квантовым числом v, а энергия уровня равна:
$E_{\mbox{кол}}=h\nu \left(v+{1\over 2} \right) \left[1-x \left(v+{1\over 2} \right) \right]$ , v=0, 1, 2, ..., (4)
где $\nu$ и x - осн. частота и постоянная ангармонизма; эти константы отличаются для различных электронных состояний. Многоатомные М, состоящие из N атомов имеют число колебательных степеней свободы $i\ge 3$ i=3N-5 для линейных М и i=3N-6 для нелинейных). Каждый колебательный У.э. в этом случае характеризуется набором колебательных квантовых чисел (v₁, v₂,..., v_i), а энергия E_кол определяется приближенным выражением:
$E_{\mbox{кол}}\approx \Sigma^i_{\mu=1} h\nu_\mu \left(v_\mu+{1\over 2} \right),\quad v_\mu=0, 1, 2, ...,$ (5)
где $\nu_\mu$ - осн. частоты (иногда их наз. частотами нормальных колебаний). Уровни колебательной энергии для М высокой степени симмтерии могут быть дважды и трижды выроженными.

Положение колебательных У.э. двухатомной М показаны на рис. 3 горизонтальными линиями у правых ветвей кривых потенциальной энергии E_кол(R). Колебательные У.э. сгущаются к границе диссоциации $E_{\mbox{эл}}(\infty)$ , но их число конечно в отличие от атомных уровней, для к-рых главное квантовое число n может принимать какие угодно большие значения. Выше границы диссоциации лежит непрерывный энергетический спектр, соответствующий диссоциированному состоянию: полная энергия свободных атомов может принимать произвольные значения.

Вращение молекул.
Вращательное движение М как целого можно приближенно рассматривать как повороты твордого тела вокруг нек-рой оси. Вращат. движение квантуется, что приводит к возникновению дискретного вращательного энергетического спектра. Каждый вращат. У.э. характеризуется вращат. энергией E_вр, вращат. МКД J, четностью P и некоторыми дополнительными квантовыми числами, к-рые часто оказываются необходимыми для описания вращения нелинейных М.

В общем случае многоатомная М имеет три главных момента инерции I₁, I₂, I₃, относительно трех взаимно перпендикулярных осей, связанных с М. Для линейной М $I_1=I_2, I_3=0$ (ось 3 в данном случае совпадает с осью М). Вращение такой М происходит вокруг оси, перпендикулярной оси М. Вращат. энергия приближенно определяется ф-лой:
$E_{\mbox{вр}} \approx {\hbar^2\over {2I_1}}\; J(J+1), \quad J=0, 1, 2,...$ (6)
Этой же ф-лой определяется энергия уровней М типа сферич. волчка, у к-рой I₁=I₂=I₃ (напр., CH₄, CF₄). Если $I_1=I_2\ne I_3$ , то М относится к типу симметричных волчков (напр., NH₃, CH₃CN). Ее У.э. характеризуются не только значениями вращат. МКД J, но и дополнительным квантовым числом - проекцией J на ось симметрии М. Эта величина обычно обозначается буквой K. Энергия вращат. У.э. в этом случае:
$E_{\mbox{вр}} \approx {\hbar^2\over {2I_1}}\; J(J+1) + {\hbar^2\over 2} \left( {1\over{I_3}} - {1\over{I_1}}\right) K^2 , \quad K=0, 1, 2,..., J$ . (7)
Если же все три момента инерции различны, М относится к типу асимметричных волчков (напр., H₂O, H₂CO). Для характеристики ее вращат. У.э. требуется задание двух дополнительных квантовых чисел, энергия вращат. уровней не может быть выражена простыми ф-лами типа (6) или (7) и рассчитывается спец. методами.

Вращат. У.э. двухатомной М в $^1\Sigma^+$ -состояниях показаны на рис. 3 для двух колебательных состояний терма $^1\Sigma^+_g$ и трех колебательных состояний терма $^1\Sigma^+_u$ . Аналогичная вращат. структура (или полоса) имеется у всех х колебательных состояний. Энергия вращат. уровней отсчитывается от положения х колебательного уровня, к-рому принадлежит данная вращат. полоса. Если М имеет тождественные ядра (как, напр., H₂), это приводит к определенным ограничениям на существования вращат. У.э. с различными значениями J. В М водорода оба ядра (протоны) имеют спины 1/2. Полный ядерный спин может принимать два значения: I=0 (параводород) и I=1 (ортоводород). В этом случае, как следует из квантовомеханич. рассмотрения, все вращат. У.э. с четными J в $^1\Sigma^+_g$ -состоянии относятся к параводороду, а в $^1\Sigma^+_u$ -состоянии - к ортоводороду. Наоборот, уровни с нечетными J в $^1\Sigma^+_g$ -состоянии относятся к ортоводороду, а в $^1\Sigma^+_u$ -состоянии - к параводороду. Четности вращат. состояний на рис. 3 указаны рядом со значениями J.

Полная энергия молекулы определяется приближенно как сумма всех видов энергии:
$E_{\mbox{мол}}\approx E_{\mbox{эл}} + E_{\mbox{кол}} + E_{\mbox{вр}}$ . (8)
Причем, как правило, выполняются неравенства
$E_{\mbox{эл}} \gg E_{\mbox{кол}} \gg E_{\mbox{вр}}$ , и
$E_{\mbox{эл}}/E_{\mbox{кол}} \approx E_{\mbox{кол}} /E_{\mbox{вр}} \approx \sqrt{m_e/m_p}$ , (9)
где m_p - масса протона.

Типы переходов в молекулах.
В соответствии со структурой энергетич. состояний в М различают три осн. типа квантовых переходов (здесь коснемся только радиац. переходов).

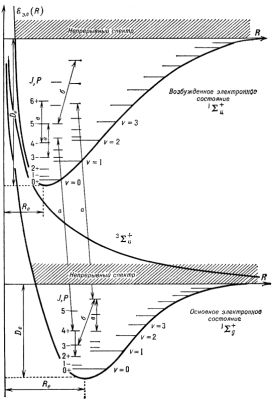
Рис. 3. Схематическое изображение структуры трех электронных
состояний орто- и парамолекул H₂. Для связанных электронных
состояний $^1\Sigma^+_g$ и $^1\Sigma^+_u$ обозначены положения
колебательных (v=0, 1, 2, ...) и вращательных (J=0, 1, 2, ...) уровней
энергии, а также их четности P. Линии со стрелками показывают
возможные типы переходов: а - электронно-колебательно-вращательные,
б - колебательно-вращательные, в - вращательные.

Электронно-колебательно-вращательные переходы (переходы типа а на рис. 3).
Длины волн этих переходов обычно лежат в УФ- и оптич. областях спектра. Для H₂ переходы типа а относятся к серии Лаймана и имеют длины волн ок. 1000-1100 ангстрем. Они наблюдаются как в межзвездной среде нашей Галактики, так и в др. галактиках и, в частности, в облаках газа, имеющих большие красные смещения. В последнем случае они могут наблюдаться методами оптич. астрономии.

Колебательно-вращательные переходы (переходы типа б на рис. 3).
Их длины волн попадают, как правило, в ИК-область спектра. Напр., колебательный переход $v=1 \to v=0$ в H₂ в осн. электронном состоянии имеет длину волны $\lambda\approx$ 2,28 мкм и наблюдается в плотных и горячих источниках связанных с областями звездообразования.

Вращательные переходы (переходы типа в на рис. 3).
Их длины волн попадают в ИК-, субмиллиметровую и микроволновую область спектра. Напр., в межзвездной среде наблюдаются вращат. переходы H₂ с длиной волны $\lambda\approx$ 28 мкм (переход $J=2 \to J=0$ ), субмиллиметровые переходы CO на волне $\lambda\approx$ 0,87 мм (переход $J=3 \to J=2$ ). Радиоастрономич. методами обнаружено более 600 вращат. линий различных межзвездных М (см. Молекулы в межзвездной среде).

Некоторые важные типы расщеплений молекулярных состояний.
Помимо осн. электронно-колебательно-вращател. структуры У.э. молекулы имеется ряд дополнит. расщеплений, играющих важную роль в интерпретации спектров межзвездных М. Кратко рассмотрим лишь нек-рые из них.

$\Lambda$ -расщепление ( $\Lambda$ -удвоение) обязано взаимодействию между вращательным и электронным движениями в М, находящихся в $\Pi,\;\Lambda$ и т.п. состояниях, т.е. когда проекция орбитального МКД электронов на ось М отлична от нуля. Важный пример этого типа расщепления приведен на рис. 4, где показана структура нижних вращател. У.э. межзвездной молекулы OH. Во внеш. электронной оболочке молекулы OH находится один электронЮ так что полный электронный спин S=1/2. Поэтому осн. состояние $^2\Pi$ расщеплено спин-орбитальным взаимодействием на две вращател. полосы: $^2\Pi_{3/2}$ и $^2\Pi_{1/2}$ . Нижний индекс у знака терма обозначает суммарную проекцию $\Omega$ орбитального и спинового МКД на ось М. В данном случае ( $\Lambda=1, \;S=1/2$ ) $\Omega$ может принимать два значения: $\Omega$ =1/2 и $\Omega$ =3/2.

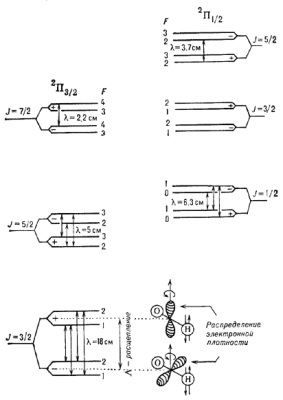
Рис. 4. Нижние уровни молекулы OH, $\Lambda$ -расщепление
и сверхтонкое расщепление. Справа внизу приведено
распределение электронной плотности, поясняющее
образование $\Lambda$ -дублета. Стрелками указаны переходы,
к-рые наблюдаются в межзвездной среде.

Т.к. для двухатомной М вращател. момент перпендикулярен молекулярной оси, то полнй МКД, слагающийся из электронного и вращател. МКД, не может быть меньше $\Omega$ . Поэтому для J возможны следующие наборы значений: J=1/2, 3/2, ... для полосы $^2\Pi_{1/2}$ и J=3/2, 5/2, ... для полосы $^2\Pi_{3/2}$ . В каждой вращател. полосе все вращател. У.э. удвоены. Причину этого удвоения качественно можно понять, рассматривая распределение электронной плотности в молекуле OH относительно оси вращения. Взаимодействие между вращательными и электронными движениями приводит к двум возможным распределениям электронной плотности, показанным в нижней части рис. 4. Моменты инерции, а следовательно, и вращател. энергии в этих двух состояниях несколько отличаются. Поэтому каждый вращател. У.э. оказывается расщепленным на два подуровня ( $\Lambda$ -удвоение), четности к-рых противоположны.

Сверхтонкое расщепление.
Если одно или неск. ядер в М имеют отличные от нуля спины, то каждый вращател. У.э. расщепляется на систему сверхтонких подуровней (сверхтонкая структура). В этом случае каждый У.э. характеризуется полным МКД молекулы (F). Напр., в молекуле OH ядро атома водорода имеет спин I=1/2, к-рый может быть направлен параллельно или антипараллельно моменту J (стрелки у атома H на рис. 4). В соответствии с правилами сложения моментов F может принимать значения $J\pm$ 1/2, к-рые указаны на рис. 4. На этом рис. указаны такэже переходы, к-рым соответствуют радиолинии молекулы OH, наблюдаемые в межзвездной среде.

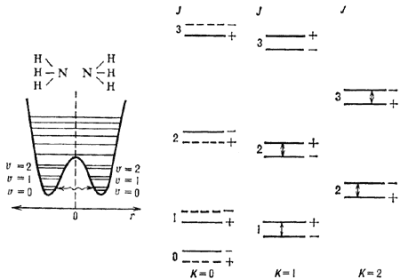
Инверсионное расщепление обязано т.н. заторможенным движениям в М. Эти движения связаны с квантовомеханическим туннельным эффектом. На рис. 5 показано осн. электронное состояние М аммиака NH₃. Кривая потенциальной энергии имеет два минимума, что соответствует двум возможным положениям атома азота относительно плоскости, в к-рой лежат атомы водорода (r- расстояние от атома азота до этой плоскости). Если атом N находится в одном из минимумов кривой потенциальной энергии , то переход в др. минимум в класси. механике энергетически невозможен. В квантовой механике такой переход возможен за счет туннельного эффекта - частица туннелирует под энергетич. барьером, что изображено волнистой линией. Т.о., два минимума потенциальной энергии оказываются связанными между собой. Согласно квантовой механике, такая связь приводит к расщеплению каждого колебательного уровня энергии, лежащего ниже центрального максимума, на два подуровня. Это расщепление наз. инверсионным. Поскольку каждому колебательному У.э. соответствует своя вращател. полоса, то двум инверсионным подуровням будут соответствовать две слегка смещенные (на величину расщепления) полосы, как это показано на рис. 5 справа, где изображен участок вращател. спектра осн. колебательного состояния аммиака. Т.к. NH₃ относится к М типа симметричного волчка, то энергии вращател. уровней можно приближенно определить по ф-ле (7) для любых J и K. М аммиака имеет три тождественных ядра. В силу принципа Паули нек-рые вращател. У.э. оказываются запрещенными (подобно тому, что имеет место для орто- и параводорода). Эти У.э. обозначены штриховыми линиями. Линии, соответствующие переходам между инверсионными подуровнями (они обозначены стрелками на рис. 5), попадают в радиодиапазон вблизи частоты 23 ГГц и наблюдаются в межзвездной среде.

Рис. 5. Структура вращательных уровней и инверсионное
расщепление в молекуле аммиака. Стрелками показаны
переходы, наблюдаемые в межзвездной среде.

Их изучение играет важную роль в исследованиях плотных и холодных облаков межзвездного газа.

4. Энергетические уровни ядер

Изотопический спин
При описании состояния атомных ядер, в дополнение к квантовым характеристикам, используемым в атомной и молекулярной спектроскопии, вводят понятие полного изотопического спина (изоспина) T и его проекции M_T. Эти величины для отдельного нуклона (t, m_t) определяют его зарядовое состояние. По определению, t=1/2, а m_t может принимать два значения: m_t=1/2 соответствует протону, m_t=-1/2 соответствует нейтрону. Полный изоспин ядра (Я) T определяется как векторная сумма изоспинов отдельных нуклонов, а его проекция M_T=(Z-N)/2, где Z - заряд Я, N - число нейтронов в Я. Напр., для пары нуклонов суммарный изоспин может принимать два значения: T=0 и T=1. Состояния с T=0, M_T=0 и T=1, M_T=0 соответствуют паре np (нейтрон-протон). Состояния с T=1, M_T=1 и T=1 M_T=-1 соответствуют парам pp и nn. От величины изоспина в общем случае зависят энергия связи и энергии уровней Я. Как правило, осн. состояние Я имеет наименьшее из допустимых значение изоспина, т.е. T_мин =|M_T|=(N-Z)/2.

Оболочечная модель ядра
Для приближенного описания дискретного энергетич. спектра атомного Я оказываются удобным, так же как и для характиристики молекулярных состояний, разделить движения в Я на внутренние и коллективные, причем последние могут быть двух типов: колебательные, соответствующие колебаниям ядерной плотности или поверхности Я, и вращательные, соответствующие вращению деформированному Я как целого вокруг оси, перпендикулярной оси деформации.

Внутреннее движение нуклонов в Я может быть приближенно описано в рамках оболочечной модели, по своим осн. представлениям аналогичной той модели, к-рая дает описание строение электронной оболочки атома. Оболочечная модель исходит из допущения, что в атомном Я каждый нуклон движется до нек-рой степени независимо в усредненном поле ядерных сил, образованном другими нуклонами. Поскольку радиус действия ядерных сил мал, это поле ограничено расстояниями порядка радиуса Я $R\approx 1,1\cdot 10^{-13} A^{1/3}$ см, где A - число частиц в Я (массовое число). Т.о., в оболочечной модели состояние Я в целом описывается перечислением состояний отдельных нуклонов. Для многих Я ср. ядерное поле обладает сферич. симметрией. Поэтому состояние отдельного нуклона в Я можно характеризовать орбитальным МКД l. Спин-орбитальное взаимодействие для такого нуклона в Я значительно больше, чем для Э в атоме. Поэтому для описания ядерных состояний используется jj-тип связи МКД. Состояния нуклонов с одинаковыми l и j нумеруют в порядке увеличения энергии числом n=1, 2,... . Различные состояния обозначают символами 1s_1/2, 1p_1/2, 1p_3/2..., где цифра перед буквой есть число n, буквы s, p, d, f, g и т.д. имеют тот же смысл, что и в атомной спектроскопии, т.е. соотвествуют значениям l=0, 1, 2, 3..., а индекс у буквы определяет величину полного МКД нуклона j.

В состоянии с заданными значениями n, l, j может находиться не более 2j+1 нуклонов каждого типа - протонов и нейтронов. Т.о., нуклонные состояния распределяются по следующим группам:

1s_1/2 2 нуклона

1p_3/2, 1p_1/2 6 нуклонов

1d_5/2, 1d_3/2, 1d_1/2 12 нуклонов

1f_7/2, 2p_3/2, 1f_5/2, 2p_1/2, 1g_9/2 30 нуклонов

2d_5/2, 1g_7/2, 1h_11/2, 2d_3/2, 3s_1/2 32 нуклона

2f_7/2, 1h_9/2, 1i_13/2, 2f_5/2, 3p_3/2, 3p_1/2 44 нуклона

Состояния в каждой группе мало отличаются по энергиям. Такие группы наз. нуклонными оболочками. Соответственно величинам, указывающим возможное число нуклонов в каждой группе, запонение к.-л. оболочки заканчивается, когда число протонов или нейтронов в Я равно одному из следующих чисел: 2, 8, 20, 50, 82, 126. Эти числа принять наз. магическими. Я, содержащие лишь заполненные протонами (или нейтронами) оболочки, наз. магическими ядрами. Я магические и по протонам и по нейтронам наз. дважды магическими. Дважды магические Я обладают особой устойчивостью по отношению к присоединению нуклона (аналогично атомам инертных газов с целиком заполненными электронными оболочками), а их первые возбужденные У.э. лежат выше, чем у остальных Я.

Большая устойчивость Я с заполненными протонными и нейтронными оболочками относительно возбуждения частично связана с эффектом спаривания нуклонов.

В четно-четных Я (т.е. в Я с четным числом протон-нейтронов) пары протонов и нейтронов с равными, но противоположно направленными спинами образуют в Я состояния типа связанных. Чтобы возбудить Я, т.е. перевести один из нуклонов пары в более высокую незаполненную оболочку, необходимо разорвать нуклонную пару, что требует значительной энергии. Полный МКД четно-четного Я в осн. состоянии равен нулю, т.к. МКД всех нуклонов попарно компенсируются.

В наиболее простом варианте оболочечной модели нечетных Я предполагается, что все нуклоны Я за исключением нечетного соединяются парами и образуют четно-четный остов. Оставшийся нечетный нуклон движется в поле этого остова. МКД такого Я равен МКД нечетного нуклона, а его энергетич. состояние определяет структуру нижних У.э. Я. Этот вариант оболочечной модели наз. одночастичной моделью Я.

С ростом энергии возбуждения расстояния между У.э. быстро уменьшаются. Энергии уровней возрастают с увеличением орбитального МКД l. При заданном l уровень с j=l+1/2 лежит глубже, чем уровень с j=l-1/2.

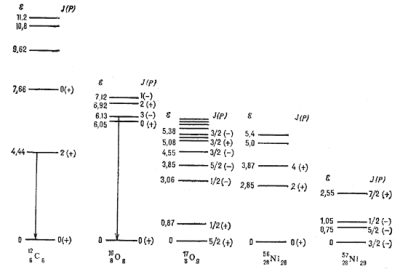
Для характеристики энергетического уровня Я обычно указывают его энергию, полный МКД J и четность P. Иногда, если это необходимо, к этим квантовым характеристикам добавляют значение изотопич. спина.

Рис. 6. Схема энергетических уровней внутренних возбуждений ядер
углерода, кислорода и никеля. Энергия E дана в МэВ. Указаны значения
полного момента ядра J и четности состояния P. Линиями со стрелками
показаны переходы, к-рые наблюдались в солнечных вспышках.

На рис. 6 приведены схемы У.э. внутр. возбуждения ядер ¹²₆C₆, ¹⁶₈O₈, ¹⁷₈O₉, ⁵⁶₂₈Ni₂₈, ⁵⁷₂₈Ni₂₉. Сравнение схем уровней для изотопов ¹⁶₈O₈, ¹⁷₈O₉, а также для ⁵⁶₂₈Ni₂₈ и ⁵⁷₂₈Ni₂₉ показывает различия в энергетич. структуре четно-четных и четно-нечетных Я. Линии, соответствующие переходам, обозначенным стрелками для Я ¹²₆C₆ (4,44 МэВ) и ¹⁶₈O₈ (6,13 МэВ), наблюдались во вспышках на Солнце. Первая из них наблюдалась также в центральной области Галактики.

Коллективные движения в ядре
Для описания этих типов движений (они становятся особенно существенными для тяжелых ядер) оболочечная модель оказывается недостаточной. Поэтому была развита обобщенная модель Я, рассматривающая движения нуклонов в незаполненных оболочках в поле остова, состоящего из нуклонов, полностью заполняющих оболочки. Спин остова равен нулю. Внеш. нуклоны при своем движении влияют на форму остова и могут деформировать его; он приобретает форму вытянутого или сплюснутого эллипсоида вращения и может колебатсья и вращаться. Эти коллективные движения нуклонов остова описываются в рамках гидродинамической модели Я.

Энергия состояния в обобщенной модели представляется суммой энергий внутреннего и коллективных движений. Под внутренним понимается движение нуклонов в незаполненных оболочках. В аксиально-симметричном поле деформированного ядра хорошей квантовой характеристикой состояния (т.е. сохраняющейся величиной) является проекция $\Omega$ полного МКД этих нуклонов на ось деформации. Полный МКД вращающегося ядра J складывается из МКД нуклонов незаполненных оболочек и МКД вращающегося остова, к-рый перпендикулярен оси деформации. Следовательно, при заданном $\Omega$ момент J может принимать значения $J=\Omega, \Omega+1, \Omega+1, ...$ , а величина вращател. энергии определяется ф-лой (6). Однако момент инерции, фигурирующий в этой ф-ле, в случае Я может считаться независимым от J лишь при небольших значениях этой величины. Когда J превышает нек-рый предел, момент инерции быстро нарастает, т.к. равновесная деформация увеличивается, что приводит к перестройке структуры У.э. Интервалы между У.э. перестают расти в соответствии с ф-лой (6), и У.э. располагаются приблизительно эквидистантно. Наконец, если Я сообщить очень большой вращател. МКД, оно может перейти в т.н. сверхвращател. состояние, к-рое явл. нестабильным. Из этого состояния Я распадается с удалением нескольких нейтронов.

Рис. 7. а - структура вращательных уровней ядра ¹⁶⁸Er,
б - структура колебательных уровней ядра ¹⁸⁸Os.
Энергия уровней дана в кэВ.

Энергетич. спектр Я., описываемый ф-лой (6), представляет собой пример простейшего спектра. Структура вращател. У.э. большинства Я имеет более сложный характер. Вращательные и колебательные переходы в Я наблюдаются в лабораторных экспериментах. Нижние вращател. У.э. отстоят от основного на десятки и сотни кэВ. Энергия колебательных возбуждений, как правило, принимает промежуточные значения между энергиями вращательных и внутренних возбуждений. На рис. 7 показаны примеры вращател. энергетич. спектра для ядра ¹⁶⁸Er (этот спектр качественно подобен тому, к-рый имеет место в молекулах типа симметричного волчка) и колебательного энергетич. спектра для ядра ¹⁸⁸₇₆Os.

Возбуждение и деактивация ядерных уровней

Возбужденное сотстояние данного Я часто возникает в результате ядерной реакции к.-л. другого Я с $\gamma$ -фотонами, Э, нуклонами, мезонами, нейтрино и др. Я. Другой путь образования возбужденного состояния - это поглощение $\gamma$ -фотона или столкновения Я с к.-л. частицей без последующей ядерной рекции (напр., кулоновское возбуждение вращательных уровней Я при столкновении с заряженной частицей). Аналогичным образом может происходить деактивация (распад) возбужденных состояний. Примером излучательной деактивации явл. распад возбужденных состояний ¹²₆C₆ и ¹⁶₈O₈ (рис. 6). Возбуждение этих У.э. в солнечных вспышках осуществляется энергичными протонами. Другим примером возбуждения и деактивации ядерных У.э. явл. реакция нейтронного захвата ¹₁H₁(n, $\gamma$ )²₁H₁, происходящая при столкновении нейтрона и протона. При этом образуется Я лейтерия не в основном, а в квазисвязанном состоянии на виртуальном У.э., к-рый расположен в непрерывном спектре вблизи границы диссоциации Я (на 0,067 МэВ выше ее). Помследующая излучательная деактивация этого уровня приводит к образованию стабильного Я дейтерия, а излученный $\gamma$ -фотон имеет энергию 2,22 МэВ. Гамма-фотоны с такой энергией также наблюдаются в солнечных вспышках. Отмеченная реакция нейтронного захвата играет большую роль в первичном космологич. нуклеосинтезе, т.к. с нее начинается цепь термоядерных реакций, приводящих к образованию Я гелия.

Лит.:
Бор О., Моттельсон Б., Структура атомного ядра, пер. с англ., т. 1-2, М., 1971-77; Борн М., Атомная физика, пер. с англ., 3 изд., М., 1970; Ельяшевич М.А., Атомная и молекулярная спектроскопия, М., 1962; Мухин К.Н., Экспериментальная ядерная физика, 3 изд., т. 1-2, М., 1974; Собельман И.И., Введение в теорию атомных спектров, М., 1977; Татевский В.М., Строение молекул, М., 1977.

(В.К. Херсонский)

В. К. Херсонский, "Физика Космоса", 1986
Глоссарий Astronet.ru

А | Б | В | Г | Д | З | И | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Э | Я

Публикации с ключевыми словами: уровни энергии - Спектр линейчатый Публикации со словами: уровни энергии - Спектр линейчатый
См. также: Линейчатое излучение (излучение в линиях) Спектр, линейчатый Спектральные классы звезд: OBAFGKM

Мнения читателей [2]

Версия для печати