Астронет > Максвелла распределение

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

На сайте

Астрометрия

Астрономические инструменты

Астрономическое образование

Астрофизика

История астрономии

Космонавтика, исследование космоса

Любительская астрономия

Планеты и Солнечная система

Солнце

Максвелла распределение

- распределение частиц (молекул, атомов) идеального газа но скоростям в условиях термодинамического (теплового) равновесия. М. р. было выведено в 1860 г. англ. физиком Дж.К. Максвеллом на основе модели, в к-рой газ рассматривается как совокупность огромного числа маленьких, абсолютно упругих шаров, находящихся в сосуде с заданной темп-рой Т стенок. Согласно М. р., ср. число частиц $\Delta n$ , имеющих абс. величину скорости в интервале от v до $v+\Delta v$ , определяется выражением:
$\Delta n=N\cdot 4\pi\cdot \left({m\over{2\pi kT}}\right)^{3/2}\cdot e^{-mv^2/2kT}\cdot v^2\cdot \Delta v$ , (*)
где N - полное число частиц в системе. М. р. получило прямое подтверждение в серии опытов с молекулярными пучками. Кроме того, закономерности протекания целого ряда физ. процессов в газах убедительно свидетельствуют о справедливости М. р. (напр., доплеровское уширение спектр. линий, особенности ионизации атомов и диссоциации молекул).

М. р. сыграло чрезвычайно важную роль в становлении и развитии кинетич. теории газов и статнстич. физики. В 1877 г. австр. физик Л. Больцман вывел более общее распределение, назваемое Больцмана распределением частиц идеального газа но энергиям. из к-рого можно получить М. р., если пренебречь всеми видами энергии, кроме кинетич. энергии частиц $\varepsilon_к=mv^2/2$ . В соответствии с (*) число частиц как с малыми, так и с очень большими скоростями мало (рис.). Максимум распределения соответствует скорости $v_н=\sqrt{2kT/m}$ (v_н - наиболее вероятная скорость). Важное физ. значение имеет ср. квадратичная скорость $\bar{v^2}=(3/2)v^2_н$ , определяющая ср. кинетич. энергию частиц $\bar{\varepsilon_{кин}}=m\bar{v^2}/2=(3/2)kT$ , к-рая не зависит от массы частиц. Поэтому в идеальном газе, состоящем из частиц различных сортов (электронов, ионов), в условиях термодинамич. равновесия все частицы, независимо от их сорта, обладают одинаковой ср. кинетич. энергией. Отсюда следует, что наибольшие скорости имеют частицы с наименьшей массой. Так, в термодинамически равновесной плазме ср. абс. величина скорости электронов e в $\sqrt{m_p/m_e}=43$ раза больше скорости протонов р, а эта последняя, в свою очередь, в 4 раза превышает скорость атомов кислорода. М. р. по одному компоненту скорости имеет гауссовский характер, т.е. его максимум приходится на нулевую скорость, а снижение кривой распределения в e раз соответствует скорости, равной $\sqrt{2kT/m}$ .

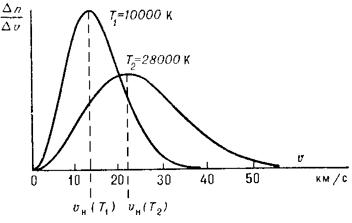
Распределение атомов ионизованного водорода
(протонов) по скоростям v при двух
значениях абсолютной температуры T₁ и T₂
(T₁ < T₂), примерно соответствующих
эффективным температурам звезд спектральных
классов АО и ВО. Полное число частиц в обоих
случаях одинаково.

Из М. р. следует, что нек-рое количество частиц может достигать скоростей, значительно превышающих v_H. Такие частицы обладают относительно большими энергиями и поэтому играют важную роль в космич. физике и астрофизике, хотя их число относительно невелико (доля частиц с абс. значением скорости $v\gg v_н$ пропорциональна $e^{v^2/v_н^2}$ ). Частицы с высокими скоростями имеют определяющее значение, напр., в диссипации атмосфер планет, в термоядерных реакциях в недрах звёзд. Как следует из определения, М. р. применимо для идеального газа, находящегося в термодинамическом равновесии. Близкие к этому требованию условия создаются для плазмы в звёздах главной последовательности. Однако на поздних стадиях эволюции звёзд в плотных ядрах красных гигантов и сверхгигантов, а также в сверхплотных объектах - белых карликах и нейтронных звёздах - св-ва звёздного вещества существенно изменяются. В этом случае частицы с полуцелым спином (электроны, нейтроны, протоны и др.) образуют вырожденный газ, описываемый более общим распределением Ферми-Дирака. С уменьшением плотности вещества при к.-л. фиксированной темп-ре, удовлетворяющей неравенству $0 < kT \ll m_e c^2$ , распределение Ферми-Дирака переходит в М. р. При звёздных взрывах (см. Гравитационный коллапс, Сверхновые звезды), а также вблизи нейтронных звёзд темп-ра вещества может быть очень высокой ( $kT \ge m_e c^2$ ) при сравнительно умеренной плотности. Здесь обычное М. р. (*) уже непригодно для электронного газа. Вместо него иногда применяют релятивистское М. р., к-рое можно получить из распределения Больцмана, воспользовавшись релятивистской связью между кинетич. энергией $\varepsilon_{кин}$ и скоростью v: $\varepsilon_{кин}=m_e c^2 (\gamma-1)$ , где $\gamma=1/\sqrt{1-(v/c)^2}$ . Однако при темп-рах $kT \ge m_e c^2$ происходит множественное рождение электрон-позитронных пар. Поэтому релятивистское М. р. можно использовать лишь в качестве первого приближения. Более точное рассмотрение должно основываться на распределении Ферми-Дирака с учётом релятивистских ф-л для импульса и энергии частиц.

М. р. широко используется для описания физ. процессов в межзвёздной и межпланетной средах. Однако не всегда вещество можно считать в этих средах находящимся в термодинамич. равновесии. Так, вследствие сильного различия масс электронов и ионов обмен энергией между ними затруднён. Поэтому часто создаются условия, когда не успевает установиться М. р., общее для электронов и ионов. Тем не менее многие астрофизич. задачи удаётся успешно решить, рассматривая электронный и ионный газы как слабо связанные системы, описываемые М. р. с различными темп-рами: электронной и ионной.

(Д.К. Надёжин)

Д. К. Надежин, "Физика Космоса", 1986
Глоссарий Astronet.ru

А | Б | В | Г | Д | З | И | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Э | Я

Публикации с ключевыми словами: распределение Максвелла Публикации со словами: распределение Максвелла
См. также: Максвелла распределение

Обсудить эту публикацию

Версия для печати