Rambler's Top100Astronet    
  по текстам   по ключевым словам   в глоссарии   по сайтам   перевод   по каталогу 		 

О кривизне пространства

О кривизне пространства

Фридман А.А.

Петроград, 29 мая 1922 г.

$1

1.В своих известных работах, посвященных общим космологическим вопросам, Эйнштейн[1] и Де-Ситтер[2] приходят к двум мыслимым типам вселенной; Эйнштейн получает так называемый цилиндрический мир, в котором пространство[3] обладает постоянной, не меняющейся с течением времени кривизной, причем радиус кривизны связывается с общей массой материи, расположенной в пространстве; Де-Ситтер получает шаровой мир, в котором уже не только пространство, но и весь мир обладает до известной степени характером мира постоянной кривизны[4]. При этом и Эйнштейн, и Де-Ситтер предполагают определенный характер тензора материи, отвечающий гипотезе несвязанности материи и ее относительному покою, иначе говоря, достаточной малости скоростей материи по сравнению с фундаментальной скоростью[5], то есть со скоростью света.

Настоящая заметка имеет целью получить цилиндрический и сферический мир как частные типы, вытекающие их некоторых общих положений, а затем показать возможность получения особого мира, кривизна которого, постоянная относительно трех принятых за пространственные координат, меняется с течением времени , т.е. зависит от четвертой координаты, принятой за временную; этот новый тип вселенной в остальных своих свойствах напоминает цилиндрический мир Эйнштейна.

2.Предположения, которые мы положим в основу наших соображений, распадаются на два класса. К первому классу относятся предположения, одинаковые с теми, которые делают Эйнштейн и Де-Ситтер и которые относятся к уравнениям, управляющим гравитационными потенциалами, и к характеру состояния и движения материи в пространстве. Ко второму классу относятся предположения об общем, так сказать, геометрическом характере нашего мира; из принятой нами гипотезы в виде частных случаев могут быть получены как цилиндрический мир Эйнштейна, так и шаровой мир Де-Ситтера.

Предположения первого класса следующие:

1)гравитационные потенциалы удовлетворяют системе уравнений Эйнштейна с так называемым «космологическим» членом, который может быть, в частности, равен нулю:

$$R_{ik} - \frac12 g_{ik} R \pm \lambda g_{ik} = -\kappa T_{ik} \ \ \ \ \ \ (i,k=1,2,3,4),$$ (A)

где $g_{ik}$ - гравитационные потенциалы, $T_{ik}$ - тензор материи, $\kappa$ - некоторая постоянная, $R=g^{ik}R_{ik}$, а тензор $R_{ik}$ определяется равенством

$$R_{ik} = \frac{\partial^2\ln{\sqrt{g}}}{\partial x_i \partial x_k} - \frac{\partial\ln{\sqrt{g}}}{\partial x_a} \left\{ ik \atop \sigma \right\} - \frac{\partial}{\partial x_{\sigma}} \left\{ ik \atop \sigma \right\} + \left\{i\alpha \atop \sigma \right\} \left\{ k\sigma \atop \alpha \right\},$$ (B)

причем $x_i$ $(i=1,2,3,4)$ - суть мировые координаты, а $\left\{ ik \atop \sigma \right\}$ - символ Кристоффеля второго рода[6];

2) материя находится в несвязанном состоянии и обладает взаимно относительным покоем; говоря менее строго, относительные скорости материи ничтожны по сравнению со скоростью света. При таких предположениях тензор материи $T_{ik}$ определяется равенствами

$T_{ik}=0$, если $i$ и $k$ одновременно не равны 4,
$T_{44}=c^2\rho g_{44}$, 		(C)

где $\rho$ - плотность материи и $c$ - фундаментальная скорость; при этом, конечно, мировые координаты разделены на две группы: $x_1,x_2,x_3$ названы пространственными координатами, а $x_4$ - временной координатой.

3. Предположения второго класса сводятся к следующему:

1) при выделении их четырех мировых координат трех пространственных ($x_1,x_2,x_3$) мы будем иметь пространство постоянной кривизны, могущей, однако, меняться с течением четвертой временной координаты $x_4$. Интервал $ds$[7], определяемый равенством , может быть написан при помощи соответствующего изменения пространственных координат в следующем виде:

$$ ds^2 = R^2(dx_1^2+\sin^2 x_1 dx_2^2 + \sin^2 x_1 \sin^2 x_2 dx_3^2) + 2g_{14} dx_1 dx_4 + 2g_{24} dx_2 dx_4 + 2g_{34} dx_3 dx_4 + g_{44} dx_4^2 \ ,$$

где $R$ есть функция только от $x_4$, $R$ пропорционален радиусу кривизны пространства; таким образом, радиус кривизны пространства может меняться с течением времени;

2) в выражении интервала $g_{14}, g_{24}, g_{34}$ обращаются в нуль при соответствующем выборе временной координаты, иначе, кратко выражаясь, время ортогонально пространству. Это второе предположение не имеет, как мне кажется, в основе своей каких-либо физических или философских соображений и вводится исключительно в целях упрощения вычислений. Необходимо заметить, что миры Эйнштейна и Де-Ситтера являются частными случаями рассматриваемого предположения.

Предположения 1) и 2) дают нам возможность записать $ds^2$ в виде

$$ds^2 = R^2 (dx_1^2 + \sin^2 x_1 dx_2^2 + \sin^2 x_1 \sin^2 x_2 dx_3^2) + M^2dx_4^2 $$ (D)

где $R$ зависит только от $x_4$, а $M$ является, вообще говоря, функцией всех четырех мировых координат. Вселенная Эйнштейна - частный случай, получаемый из формулы (D) заменой $R^2$ на $-R^2/c^2$ и $M$ на 1, где $R$ - постоянный (не зависящий от $x_4$!) радиус кривизны пространства. Вселенная Де-Ситтера получается, когда в формуле (D) заменим $R^2$ на $-R^2/c^2$, а $T$ - на $\cos{x_4}$:

$$ d\tau^2 = -\frac{R}{c^2} (dx_1^2 + \sin^2 x_1 dx_2^2 + \sin^2 x_1 \sin^2 x_2 dx_3^2) + dx_4^2$$ (D1)
$$ d\tau^2 = -\frac{R^2}{c^2} (dx_1^2 + \sin^2 x_1 dx_2^2 + \sin^2 x_1 \sin^2 x_2 dx_3^2) + \cos^2 x_1 dx_4^2 $$ (D2)

(Придавая интервалу $ds$ размер времени, мы обозначим его через $d\tau$; в этом случае постоянная $\kappa$ будет иметь размерностью длину, деленную на массу и в единицах CGS будет равна $1.87\cdot10^{-27}$)

4. Необходимо сказать еще несколько слов о тех интервалах, в которых заключены мировые координат; иначе говоря, необходимо условиться, какие точки многообразия четырех измерений мы будем считать за различные. Не входя в более подробные пояснения, условимся пространственные координаты изменять в следующих интервалах: $x_1$ - в интервале $(0,\pi)$, $x_2$ - в интервале $(0,\pi)$, $x_3$ - в интервале $(0,2\pi)$, что же касается временной координаты, то вопрос об интервале изменения ее оставим открытым. к нему мы вернемся в дальнейшем.

$2

1.Пользуясь уравнениями (A) и (B) в предположении, что гравитационные потенциалы определяются равенством (D), и полагая в уравнениях (A), что $i=1,2,3$, $k=4$, найдем

$$ R'(x_4)\frac{\partial M}{\partial x_1} = R'(x_4)\frac{\partial M}{\partial x_2} = R'(x_4) \frac{\partial M}{\partial x_3}.$$

Эти равенства имеют два случая: 1) $R'(x_4)=0$, $R$ не зависит от $x_4$ и является постоянной; назовем этот случай стационарным миром, и 2) $R'(x_4)\neq 0$, $M$ зависит только от $x_4$; назовем этот случай нестационарным миром.

Обращаясь сначала к стационарному миру, выпишем уравнения (A) для $i,k=1,2,3$ в предположении различных индексов; уравнения эти дадут нам следующую систему формул:

$$ \frac{\partial^2M}{\partial x_1 \partial x_2} - \ctg x_1 \frac{\partial M}{\partial x_2} = 0 ,$$
$$ \frac{\partial^2M}{\partial x_1 \partial x_3} - \ctg x_1 \frac{\partial M}{\partial x_3} = 0 ,$$
$$ \frac{\partial^2M}{\partial x_2 \partial x_3} - \ctg x_2 \frac{\partial M}{\partial x_3} = 0 .$$

Интегрируя эти уравнения, найдем

$$ M = A(x_3,x_4) \sin x_1 \sin x_3 + B(x_3,x_4) \sin x_1 + C(x_1,x_4),$$ (1)

где $A,B,C$ - произвольные функции своих аргументов. Разрешая обычными приемами уравнения (A) относительно тензора , исключая из неучтенных и неиспользованных еще уравнений неизвестную плотность[8] и подставляя выражение (1) для $M$ в эти уравнения, мы после длинных, но элементарных вычислений найдем, что для $M$ возможны следующие два выражения:

$$M=M_0=\mbox{const},$$ (2)
$$M=(A_0x_4+B_0)\cos x_1,$$ (3)

где $M_0,A_0,B_0$ - постоянные величины.

В случае, когда $M$ равно постоянному числу, мы имеем для стационарного мира случай цилиндрического мира. При этом удобнее оперировать гравитационными потенциалами, получаемыми из формулы (D); определяя плотность и величину $\lambda$, получим известный результат Эйнштейна:

$$ \lambda=\frac{c^2}{R^2},\quad \rho=\frac2{\kappa R^2},\quad M=\frac{4\pi^2}{\kappa}R $$

где $M$ - общая масса всего пространства.

В другом возможном случае, когда $M$ определяется из формулы (3), мы при помощи рационального изменения $x_4$[9] приходим к шаровому миру Де-Ситтера, в котором $M=\cos x_1$; пользуясь формулой D2, найдем следующие соотношения Де-Ситтера:

$$ \lambda=\frac{3c^2}{R^2}, \quad \rho=0, \quad M=0 .$$

Таким образом, стационарный мир может быть или цилиндрическим миром Эйнштейна, или сферическим миром Де-Ситтера.

2. Обратимся теперь к изучению другого возможного мира - нестационарного. В этом случае $M$ есть функция только $x_4$; соответственно изменяя $x_4$, мы можем без ограничения общности положить $M=1$; имея в виду большие удобства наших обычных представлений, напишем $ds^2$ в форме, аналогичной (D1) и (D2):

$$ ds^2 = -\frac{R^2(x_4)}{c^2} (dx_1^2 + \sin^2 x_1 dx_2^2 + \sin^2 x_1 \sin^2 x_2 dx_3^2) + dx_4^2 .$$ (D3)

Нашей задачей является определение $R$ и $\rho$ из уравнений (A). Очевидно, что уравнения (A), в которых значки различны, ничего не дадут; уравнения (A), в которых $i=k=1,2,3$, дадут одно соотношение:

$$ \frac{R'^2}{R^2}+\frac{2RR''}{R^2}+\frac{c^2}{R^2}-\lambda=0 ,$$ (4)

а уравнение (A), в котором $i=k=4$, даст равенство

$$ \frac{3R'^2}{R^2}+\frac{3c^2}{R^2}-\lambda=\kappa c^2\rho ,$$ (5)

причем

$$ R'=\frac{dR}{dx_4}, \quad R''=\frac{d^2R}{dx_4^2} .$$

Так как $R''\neq0$, то интегрирование уравнения (4) после замены для удобства $x_4$ на $t$ даст нам уравнение

$$ \frac1{c^2}\left(\frac{dR}{dt}\right)^2=\frac{A-R+\frac{\lambda}{3c^3}R^3}{R} ,$$ (6)

где $A$ - произвольная постоянная. Из этого уравнения $R$ получается путем обращения некоторого эллиптического интеграла, т.е. путем решения относительно $R$ уравнения

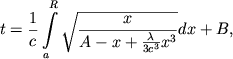$$ t=\frac1c\int\limits_a^R\sqrt{ \frac{x}{A-x+\frac{\lambda}{3c^3}x^3} }dx+B,$$ (7)

где $B$ и $a$ - постоянные; при этом, конечно, надо помнить об обычных изменения знака у квадратного корня.

Уравнение (5) дает нам возможность определить $\rho$:

$$ \rho=\frac{3A}{\kappa R^3} $$ (8)

через всю массы $M$ пространства; постоянная $A$ выразится равенством

$$ A=\frac{\kappa M}{6\pi^2} ,$$ (9)

принимая, что масса $M$ - величина положительная, мы и для $A$ получим положительное значение.

3. Изучение нестационарного мира основано на изучении уравнений (6) и (7); при этом, конечно, величина $\lambda$ не определяется сама собой, и мы при изучении уравнений (6) и (7) будем предполагать, что $\lambda$ может принимать любые значения. Определим те значения переменной $x$, при которых квадратный корень, входящий в формулу (7), может изменить свой знак. Ограничиваясь случаем положительного радиуса кривизны, нам достаточно рассмотреть значения для $x$, при которых подкоренное выражение обращается в нуль или бесконечность в интервале $(0,\infty)$ для $x$, т.е. для положительных $x$.

Одно из значений $x$, при котором квадратный корень в формуле (7) обращается в нуль, есть значение $x=0$; другие значения $x$, при которых квадратный корень в формуле (7) может изменять свой знак, определятся при изучении положительных корней уравнения

$$ A-x+\frac{\lambda}{3c^3}x^3=0 .$$

Обозначая $\lambda/3c^3$ через $y$, построим семейство кривых третьего порядка в плоскости (x,y), определяемое уравнением

$$ yx^3-x+A=0 ,$$ (10)

где $A$ - параметр семейства, меняющийся в интервале . Кривые нашего семейства, показанные на рисунке, пересекают ось $x$ в точке $x=A, y=0$ и имеют максимум в точке

$$ x=\frac{3A}{2},\quad y=\frac{4}{27A^2} .$$

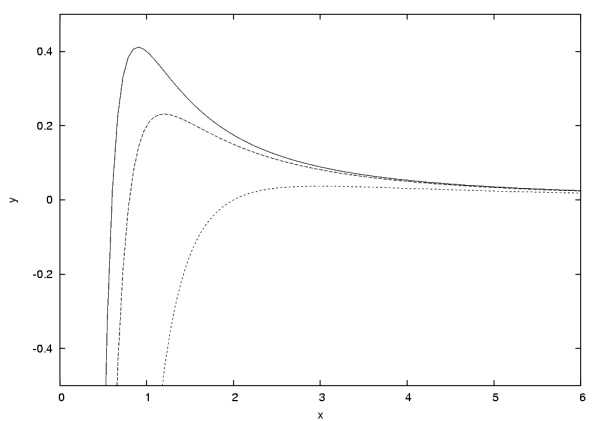
Рассмотрение чертежа показывает, что при отрицательных $\lambda$ уравнение $A-x+(\lambda/3c^3)x^3=0$ имеет один положительный корень $x_0$, лежащий в интервале $(0,A)$; рассматривая $x_0$ как функцию $\lambda$ и $A$:

$$ x_0=\theta(\lambda,A) ,$$

найдем, что $\theta$ - возрастающая функция от $\lambda$ и возрастающая функция от $A$. Далее, если $\lambda$ лежит в интервале , то уравнение наше будет иметь два положительных корня: и $x'_0=\phi(\lambda,A)$, причем $x_0$ лежит в интервале $(A,\frac32A)$, а $x'_0$ - в интервале $(\frac32A,\infty)$; $\theta(\lambda,A)$ будет возрастающей функцией как от $\lambda$, так и от $A$; будет убывающей функцией от $\lambda$ и от $A$. Наконец, если $\lambda$ больше $\frac49(c^2/A^2)$, то наше уравнение не будет иметь положительных корней.

Приступая к исследованию формулы (7), сделаем одно замечание: пусть в начальный момент , т.е. при $t=t_0$, радиус кривизны равен $R_0$. В этот начальный момент квадратный корень, стоящий в формуле (7), будет иметь знак плюс или минус, смотря по тому, возрастает ли радиус кривизны с течением времени при $t=t_0$ или нет. Изменяя время $t$ на $-t$, мы всегда можем приписать этому квадратному корню знак плюс, иначе говоря, без ограничения общности, можем время выбрать так, чтобы радиус кривизны в рассматриваемый начальный момент $t=t_0$ возрастал с течением времени.

4. Рассмотрим случай, когда , когда, следовательно, уравнение $A-x+(\lambda/3c^3)x^3 = 0$ не имеет положительных корней. В этом случае уравнение (7) перепишется следующим образом:

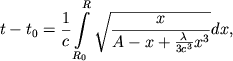$$ t-t_0=\frac1c\int\limits_{R_0}^{R}\sqrt{ \frac{x}{A-x+\frac{\lambda}{3c^3}x^3} }dx ,$$ (11)

причем, согласно замечанию, сделанному в конце предыдущего пункта, квадратный корень будет всегда положителен. Отсюда следует, что $R$ будет возрастающей функцией от $t$; на начальное значение радиуса кривизны $R_0$ никаких в этом случае ограничений не налагается.

Так как радиус кривизны не может быть меньше нуля, то, уменьшаясь от $R_0$ с уменьшением $t$ согласно формуле (11), радиус кривизны через некоторый промежуток времени $t'$ дойдет до нуля. Пользуясь очевидной аналогией, будем называть промежуток времени, понадобившийся, чтобы радиус кривизны от $0$ дошел до $R_0$, временем, прошедшим от сотворения мира[10]; этот промежуток $t'$ определяется равенством

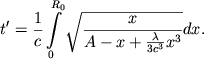$$ t'=\frac1c\int\limits_0^{R_0}\sqrt{ \frac{x}{ A-x+\frac{\lambda}{3c^3}x^3 } } dx .$$ (12)

Условимся в дальнейшем рассматриваемый мир называть монотонным миром первого рода.

Время, прошедшее от сотворения монотонного мира первого рода, рассматриваемое как функция $R_0,A,\lambda$, обладает следующими свойствами: 1) оно возрастает с увеличением $R_0$; 2) оно убывает с увеличением $A$, то есть с увеличением массы материи пространства; 3) оно убывает с увеличением $\lambda$. Если $A>\frac23 R_0$ , то при любых $\lambda$ время, протекшее от «сотворения мира», конечно, если $A \leq \frac23R_0$, то всегда найдется такое характеристическое значение $\lambda=\lambda_1=\frac49 (c^2/A^2)$, что с приближением $\lambda$ к этой величине время, прошедшее от «сотворения мира», будет беспредельно возрастать.

5. Положим далее, что $\lambda$ заключено в интервале $(0,\frac49(c^2/A^2))$; тогда начальное значение радиуса кривизны $R_0$ может лежать в одном из трех интервалов: $(0,x_0),(x_0,x'_0),(x'_0,\infty)$. Если $R_0$ лежит в интервале $(x_0,x'_0)$, то квадратный корень в формуле (7) имеет мнимое значение и пространство с такой начальной кривизной не может существовать. Случай, когда $R_0$ лежит в интервале $(0,x_0)$, мы рассмотрим в следующем пункте, теперь же остановимся на третьем случае, когда $R_0>x'_0$ или $R_0>\phi(\lambda,A)$. В этом случае рассуждениями, аналогичными приведенным в предыдущем пункте, можно показать, что $R$ будет возрастающей функцией времени, причем $R$ может меняться, начиная с $x'_0=\phi(\lambda,A)$; промежуток времени, прошедший с момента, когда $R=x_0$, до момента $R=R_0$, назовем временем, протекшим от «сотворения мира», и обозначим через $t'$:

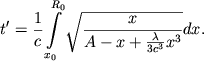$$ t'=\frac1c\int\limits_{x_0}^{R_0}\sqrt{ \frac{x}{ A-x+\frac{\lambda}{3c^3}x^3 } } dx .$$ (13)

Условимся рассматриваемый мир называть монотонным миром второго рода.

6. Рассмотрим, наконец, случай, когда $\lambda$ заключено в интервале $(-\infty,0)$. В этом случае, если $R_0>x_0=\theta(\lambda,A)$, то квадратный корень в формуле (7) становится мнимым, и, следовательно, пространство с указанным радиусом кривизны не может существовать. Если $R_0 \lt x_0$, то рассматриваемый случай будет совершенно одинаков со случаем, опущенным при рассмотрении в предыдущем пункте. Итак, положим, что $\lambda$ лежит в интервале $(-\infty,\frac49(c^2/A^2))$, а $R_0 \lt x_0$. Обычными рассуждениями[11] можно в этом случае показать, что $R$ будет периодической функцией от $t$ с периодом $t_p$, который мы назовем периодом мира и который будет определен равенством

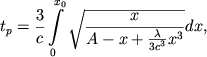$$ t_p=\frac3c\int\limits_0^{x_0}\sqrt{ \frac{x}{ A-x+\frac{\lambda}{3c^3}x^3 } } dx ,$$ (14)

причем радиус мира будет меняться от нуля до $x_0$. Условимся такого рода мир называть периодическим. Период периодического мира возрастает с возрастанием $\lambda$, стремясь к бесконечности, когда $\lambda$ стремится к $\lambda_1=\frac49(c^2/A^2)$.

При малых $\lambda$ период $t_p$ определяется приблизительной формулой

$$t_p=\frac{\pi A}{c}$$ (15)

На периодический мир можно смотреть с двух точек зрения. Если считать два явления совпадающими, коль скоро совпадают пространственные координаты, а временные отличаются на целое число периодов, то радиус кривизны мира, увеличиваясь сначала от $0$ до $x_0$, будет затем уменьшаться до нуля: тогда время существования мира будет конечным.

С другой стороны, если изменять время от $-\infty$ до $\infty$, т.е. если считать два явления совпадающими, коль скоро совпадают не только их пространственные координаты, но и их временные координаты, то мы придем к действительной периодичности кривизны пространства.

7. Данные, которыми мы располагаем, совершенно недостаточны для каких-либо численных подсчетов и для решения вопроса о том, каким миром является наша вселенная; быть может, проблема причинности и проблема центробежной силы прольют свет на рассматриваемые здесь вопросы. Следует отметить, что в полученных нами формулах «космологическая» величина $\lambda$ не определяется, являясь лишней константой задачи; быть может, электродинамические соображения смогут определить эту величину. Полагая $\lambda=0$ и считая $M$ равной массе $5\cdot10^{21}$ наших Солнц, будем для периода мира иметь величину порядка 10 миллиардов лет.

Эти цифры могут иметь, конечно, лишь иллюстративное значение.

1. Einstein A., Kosmologische Betrachtungen zur allgemien Relativistatstheorie, Sitzungsber, Dtsch. Akad. Berlin 1917
2. De-Sitter, On Einstein's theory of gravitation and its astronomical consequences, Monthly Notices Roy. Astron. Soc., 1916-1917
3. Под «пространством» будем подразумевать пространство, описываемое многообразием трех измерений, относя термин «мир» к пространству, описываемому многообразием четырех измерений
4. Klein F., Ueber die Integralform der Erhaltung ersatze und die Theorie der raumlichgeschlossen Welt, Gottinger Nach., 1918
5. См. этот термин у Эддингтона в книге Espace, Temps et Gravitation, 2 Partie. Paris, 1921, p.10
6. Знак $R_{ik}$ и скалярной кривизны $R$ изменен на обратный сравнительно с обычным обозначением этой величины.
7. A. Eddington. Espace, Temps et Gravitation, 2 partie, Paris, 1921.
8. Плотность $\rho$ является у нас неизвестной функцией мировых координат $x_1,x_2,x_3,x_4$
9. Указанное изменение производится с помощью формулы: $d\tilde{x}_4=\sqrt{A_0x_4+B_0}dx_4$
10. Время, прошедшее от сотворения мира, характеризует время, прошедшее от момента, когда пространство было точкой ($R=0$) до нынешнего его состояния ($R=R_0$)ж это время может быть бесконечным.
11. См., например, Weierstrass K. Ueber eine Gattung der reel periodischer Functionen, Monastber. Konigl. Akad. Wiss., 1866, а также Zur Theorie der kleinen endlichen Schwingungen, Z. Math. und Phys., 1902, 47. В нашем случае необходимо, конечно, внести некоторые видоизменения в рассуждения цитированных авторов; впрочем, периодичность в нашем случае устанавливается путем элементарного рассмотрения
Публикации с ключевыми словами: гравитация - Космология
Публикации со словами: гравитация - Космология
См. также:
Все публикации на ту же тему >>

Обсудить эту публикацию
Оценка: 3.0 [голосов: 74]
 
О рейтинге
Версия для печати Распечатать

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам

Комментарии, вопросы? Пишите: info@astronet.ru или сюда

Rambler's Top100 Яндекс цитирования