Астронет > Колебания и волны

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

Затухание колебаний.

Если энергия не подводится извне, то колебания связанных осцилляторов будут затухать. Поскольку сила вязкого трения пропорциональна скорости, то уравнения (3.21) с учетом затухания примут вид:

(3.34)

$\begin{array}{l} \ddot {\displaystyle s}_{1} = - \omega _{1}^{2} s_{1} - 2\delta _{1} \dot {\displaystyle s}_{1} - \alpha _{1} s_{2} , \\ \ddot {\displaystyle s}_{2} = - \alpha _{2} s_{1} - \omega _{2}^{2} s_{2} - 2\delta _{2} \dot {\displaystyle s}_{2} . \\ \end{array}$

Здесь $\delta _{1} = \Gamma _{1} / 2m_{1}$ и $\delta _{2} = \Gamma _{2} / 2m_{2}$ - коэффициенты затухания для первого и второго осцилляторов. Если искать решение этой системы в виде нормальных затухающих колебаний:

(3.35)

$s_{1} \left( {\displaystyle t} \right) = s_{01} e^{ - \delta t}\sin \left( {\displaystyle \omega t + \varphi } \right), \quad s_{2} \left( {\displaystyle t} \right) = s_{02} e^{ - \delta t}\sin \left( {\displaystyle \omega t + \varphi } \right),$

то после подстановки (3.35) в (3.34) можно найти нормальную частоту $\omega$ , коэффициент затухания $\delta$ и конфигурацию $\varsigma$ каждой из двух мод. Опуская промежуточные выкладки, отметим, что при $\omega _{1} \gg \delta _{1}$ и $\omega _{2} \gg \delta _{2}$ (слабое затухание) нормальные частоты и распределение амплитуд в модах будут близки к тем, что и в отсутствие затухания. Для коэффициента затухания $\delta$ получается выражение:

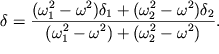(3.36)

$\delta = {\displaystyle \frac{\displaystyle {\displaystyle (\omega _{1}^{2} - \omega ^{2})\delta _{1} + (\omega _{2}^{2} - \omega ^{2})\delta _{2} }}{\displaystyle {\displaystyle (\omega _{1}^{2} - \omega ^{2}) + (\omega _{2}^{2} - \omega ^{2})}}}.$

Можно видеть, что при произвольном соотношении между $\omega _{1} , \omega _{2} , \delta _{1}$ и $\delta _{2}$ коэффициенты затухания мод $\delta _{I}$ и $\delta _{II} ,$ получаемые из (3.36) при $\omega = \omega _{I}$ и $\omega = \omega _{II} ,$ будут различными.

Если парциальные частоты совпадают $(\omega _{1} = \omega _{2} ),$ то

(3.37)

$\delta _{I} = \delta _{II} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}\left( {\displaystyle \delta _{1} + \delta _{2} } \right).$

Если $\omega _{1} \ne \omega _{2} ,$ а $\delta _{1} = \delta _{2} = \delta ,$ то

(3.38)

$\delta _{I} = \delta _{II} = \delta .$

Последним результатом мы воспользуемся при рассмотрении диссипации энергии в связанной колебательной системе.

Энергия колебательной системы и ее диссипация.

Рассмотрим колебания двух одинаковых масс (рис. 3.10а), закрепленных на растянутом легком резиновом шнуре.

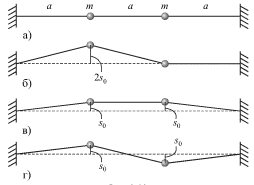Рис. 3.10.

Если один из грузов оттянуть на расстояние $2s_{0}$ (б) и затем одновременно отпустить обе массы, то их колебания будут иметь вид биений. С другой стороны, при этих начальных условиях будут возбуждены две моды (в и г) с одинаковыми амплитудами колебаний обеих масс, равными $s_{0} .$ Энергия, запасенная в первой моде, равна сумме кинетических энергий обеих масс при прохождении ими положения равновесия со скоростью $v_{0}^{I} = s_{0} \omega _{I} ,$ т.е.:

(3.39а)

$E_{0}^{I} = 2{\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle 2}}}(v_{0}^{I} )^{2} = ms_{0}^{2} \omega _{I}^{2} ,$

а энергия второй моды, аналогично, равна

(3.39б)

$E_{0}^{II} = 2{\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle 2}}}(v_{0}^{II} )^{2} = ms_{0}^{2} \omega _{II}^{2} .$

Важно отметить, что энергообмен между модами отсутствует, а полная энергия системы равна сумме энергий ее мод. В то же время в процессе биений энергия первого осциллятора за время, равное половине периода биений, "перетекает" ко второму осциллятору и затем за такое же время возвращается обратно. Полный энергообмен между осцилляторами возможен лишь тогда, когда обе массы одинаковы и отношение $(\omega _{I} + \omega _{II} ) / (\omega _{II} - \omega _{I} )$ равно целому числу $n,$ т.е.:

(3.40)

${\displaystyle \frac{\displaystyle {\displaystyle \omega _{I} + \omega _{II} }}{\displaystyle {\displaystyle \omega _{II} - \omega _{I} }}} = {\displaystyle \frac{\displaystyle {\displaystyle 2\omega _{0} }}{\displaystyle {\displaystyle \Omega _{б} }}} = n.$

Следовательно, частота $\omega _{0}$ должна быть кратной частоте биений. В самом деле, при выполнении условия (3.40) каждая из масс будет периодически останавливаться в положении равновесия (как следует из формул (3.17)). С течением времени колебания будут затухать, и будет экспоненциально уменьшаться энергия, запасенная в модах:

(3.41а)

$E^{I}(t) = ms_{0}^{2} e^{ - 2\delta t}\omega _{I}^{2} = E_{0}^{I} e^{ - 2\delta t},$

(3.41б)

$E^{II}(t) = ms_{0}^{2} e^{ - 2\delta t}\omega _{II}^{2} = E_{0}^{II} e^{ - 2\delta t}.$

Важно подчеркнуть, что через время $\tau _{E} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2\delta }}}$ энергия каждой из мод уменьшится в е раз, при этом противофазная мода "потеряет" больше энергии, чем синфазная, поскольку начальная энергия $E_{0}^{II}$ у нее была больше, чем $E_{0}^{I}$ (см. (3.39)).

Вынужденные колебания.

Рассмотрим основные закономерности вынужденных установившихся колебаний в системе, изображенной на рис. 3.11, если на левую массу $m_{1}$ действует сила $F\left( {\displaystyle t} \right) = F_{0} \sin \omega t.$ Уравнения движения в этом случае будут отличаться от (3.34) наличием этой силы в правой части первого уравнения:

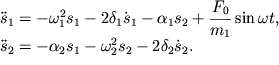(3.42)

$\begin{array}{l} \ddot {\displaystyle s}_{1} = - \omega _{1}^{2} s_{1} - 2\delta _{1} \dot {\displaystyle s}_{1} - \alpha _{1} s_{2} + {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle m_{1} }}}\sin \omega t, \\ \ddot {\displaystyle s}_{2} = - \alpha _{2} s_{1} - \omega _{2}^{2} s_{2} - 2\delta _{2} \dot {\displaystyle s}_{2} . \\ \end{array}$

Нетрудно догадаться, что решениями этой системы в установившемся режиме являются гармонические функции

(3.43)

$s_{1} (t) = s_{01} \sin (\omega t + \varphi _{1} ), \quad s_{2} (t) = s_{02} \sin (\omega t + \varphi _{2} ),$

которые отражают тот факт, что обе массы колеблются на частоте вынуждающей силы. Подставляя (3.43) в (3.42), можно вычислить амплитуды и фазы вынужденных колебаний. Мы ограничимся лишь обсуждением результатов.

Рис. 3.11.

На рис. 3.12 изображена АЧХ для первого осциллятора, к которому приложена сила. Обращает на себя внимание наличие двух резонансов, которые при малом затухании наблюдаются на нормальных частотах $\omega _{I}$ и $\omega _{II}$ . При изменении частоты $\omega$ от $\omega _{I}$ до $\omega _{II}$ амплитуда $s_{01}$ падает и достигает минимума на второй парциальной частоте $\omega _{2} ,$ при этом с уменьшением затухания амплитуда на этой частоте стремится к нулю. Это обстоятельство используют для подавления отклика системы на действие внешней силы. В радиотехнике, где используются связанные колебательные контуры, их применяют как фильтры и демпферы.

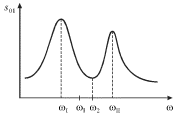Рис. 3.12.

Два резонанса имеют место и для смещения $s_{2}$ второй массы. Если проанализировать отношение амплитуд $s_{02} / s_{01}$ в зависимости от частоты $\omega ,$ то оказывается, что это отношение вблизи частоты $\omega _{I}$ равно коэффициенту распределения амплитуд $\varsigma _{I}$ для первой моды, а вблизи частоты $\omega _{II}$ - коэффициенту распределения амплитуд $\varsigma _{II}$ для второй моды. Это используется для определения этих коэффициентов, поскольку при вынужденных колебаниях это сделать проще, чем при собственных.

Назад| Вперед

Публикации с ключевыми словами: колебания - волны Публикации со словами: колебания - волны
См. также: Эхо из глубин красного гиганта

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце