Астронет > Механика твердого тела. Лекции.

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Механика твердого тела. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 1997 г. Содержание

Лекция 3.

Динамика абсолютно твердого тела. Уравнение поступательного движения и уравнение моментов. Вращение твердого тела вокруг неподвижной оси. Центр удара. Динамика плоского движения твердого тела. Движение аксиально симметричного твердого тела, закрепленного в центре масс. Уравнения Эйлера.

Уравнения динамики твердого тела. Общий случай.

В общем случае абсолютно твердое тело имеет 6 степеней свободы, и для описания его движения необходимы 6 независимых скалярных уравнений или 2 независимых векторных уравнения.

Вспомним, что твердое тело можно рассматривать как систему материальных точек, и, следовательно, к нему применимы те уравнения динамики, которые справедливы для системы точек в целом.

Обратимся к опытам.

Возьмем резиновую палку, утяжеленную на одном из концов и имеющую лампочку точно в центре масс (рис. 3.1). Зажжем лампочку и бросим палку из одного конца аудитории в другой, сообщив ей произвольное вращение - траекторией лампочки будет при этом парабола - кривая, по которой полетело бы небольшое тело, брошенное под углом к горизонту.

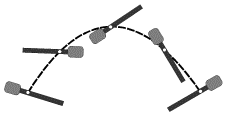Рис. 3.1.

Стержень, опирающийся одним из концов на гладкую горизонтальную плоскость (рис.1.16), падает таким образом, что его центр масс остается на одной и той же вертикали - нет сил, которые сдвинули бы центр масс стержня в горизонтальном направлении.

Опыт, который был представлен на рис. 2.2 а, в, свидетельствует о том, что для изменения момента импульса тела существенна не просто сила, а ее момент относительно оси вращения.

Тело, подвешенное в точке, не совпадающей с его центром масс (физический маятник), начинает колебаться (рис. 3.2а) - есть момент силы тяжести относительно точки подвеса, возвращающий отклоненный маятник в положение равновесия. Но тот же маятник, подвешенный в центре масс, находится в положении безразличного равновесия (рис. 3.2б).

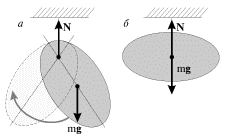Рис. 3.2.

Роль момента силы наглядно проявляется в опытах с "послушной" и "непослушной" катушками (рис. 3.3). Плоское движение этих катушек можно представить как чистое вращение вокруг мгновенной оси, проходящее через точку соприкосновения катушки с плоскостью. В зависимости от направления момента силы F относительно мгновенной оси катушка либо откатывается (рис. 3.За), либо накатывается на нитку (рис. 3.Зб). Держа нить достаточно близко к горизонтальной плоскости, можно принудить к послушанию самую "непослушную" катушку.

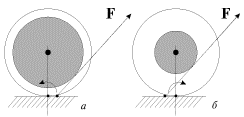Рис. 3.3.

Все эти опыты вполне согласуются с известными законами динамики, сформулированными для системы материальных точек: законом движения центра масс и законом изменения момента импульса системы под действием момента внешних сил. Таким образом, в качестве двух векторных уравнений движения твердого тела можно использовать:

Уравнение движения центра масс

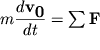$m{\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf v}_{{\displaystyle \bf 0}} }}{\displaystyle {\displaystyle dt}}} = \sum {\displaystyle {\displaystyle \bf F}}$

(3.1)

Здесь $\bf v}_{{\displaystyle \bf 0}$ - скорость центра масс тела, $\sum {\displaystyle {\displaystyle \bf F}}$ - сумма всех внешних сил, приложенных к телу.

Уравнение моментов

$\frac{\displaystyle {\displaystyle d{\displaystyle \bf L}}}{\displaystyle {\displaystyle dt}}} = \sum {\displaystyle {\displaystyle \bf M}$

(3.2)

Здесь L- момент импульса твердого тела относительно некоторой точки, $\sum {\displaystyle {\displaystyle \bf M}}$ - суммарный момент внешних сил относительно той же самой точки.

К уравнениям (3.1) и (3.2), являющимся уравнениями динамики твердого тела, необходимо дать следующие комментарии:

1. Внутренние силы, как и в случае произвольной системы материальных точек, не- влияют на движение центра масс и не могут изменить момент импульса тела.

2. Точку приложения внешней силы можно произвольно перемещать вдоль линии, по которой действует сила. Это следует из того, что в модели абсолютно твердого тела локальные деформации, возникающие в области приложения силы, в расчет не принимаются. Указанный перенос не повлияет и на момент силы относительно какой бы то ни было точки, так как плечо силы при этом не изменится.

Векторы L и M в уравнении (3.2), как правило, рассматриваются относительно некоторой неподвижной в лабораторной системе XYZ точки. Во многих задачах L и M удобно рассматривать относительно движущегося центра масс тела. В этом случае уравнение моментов имеет вид, формально совпадающий с (3.2). В самом деле, момент импульса тела $\bf L}_{0$ относительно движущегося центра .масс О связан с моментом импульса $\bf L}_{{\displaystyle 0}'$ относительно неподвижной - точки O' соотношением, полученным в конце лекции 2:

${\displaystyle \bf L}_{0} = {\displaystyle \bf L}_{{\displaystyle 0}'} - {\displaystyle \bf R}\times {\displaystyle \bf p},$

(3.3)

где R - радиус-вектор от O' к О, p - полный импульс тела. Аналогичное соотношение легко может быть получено и для моментов силы:

${\displaystyle \bf M}_{0} = {\displaystyle \bf M}_{{\displaystyle 0}'} - {\displaystyle \bf R}\times {\displaystyle \bf F},$

(3.4)

где F - геометрическая сумма всех сил, действующих на твердое тело.

Поскольку точка O' неподвижна, то справедливо уравнение моментов (3.2):

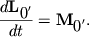${\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf L}_{{\displaystyle 0}'} }}{\displaystyle {\displaystyle dt}}} = {\displaystyle \bf M}_{{\displaystyle 0}'} .$

(3.5)

Тогда

$\frac{\displaystyle {\displaystyle d{\displaystyle \bf L}_{0} }}{\displaystyle {\displaystyle dt}}} = \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf L}_{{\displaystyle 0}'} }}{\displaystyle {\displaystyle dt}}} - {\displaystyle \bf R}\times {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf p}}}{\displaystyle {\displaystyle dt}}}} \right) - {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf R}}}{\displaystyle {\displaystyle dt}}}\times {\displaystyle \bf p} = \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf L}_{{\displaystyle 0}'} }}{\displaystyle {\displaystyle dt}}} - {\displaystyle \bf R}\times {\displaystyle \bf F}} \right) - {\displaystyle \bf v}_{{\displaystyle \bf 0}} \times {\displaystyle \bf p$

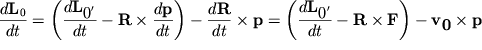(3.6)

Здесь учтено, что {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf p}}}{\displaystyle {\displaystyle dt}}} = {\displaystyle \bf F}.

Величина $\bf v}_{{\displaystyle \bf 0}} = {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf R}}}{\displaystyle {\displaystyle dt}}$ есть скорость точки О в лабораторной системе XYZ. Учитывая (3.4), получим

${\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf L}_{0} }}{\displaystyle {\displaystyle dt}}} = {\displaystyle \bf M}_{0} - {\displaystyle \bf v}_{{\displaystyle \bf 0}} \times {\displaystyle \bf p}.$

(3.7)

Поскольку движущаяся точка O - это центр масс тела, то $\bf p} = m{\displaystyle \bf v}_{{\displaystyle \bf 0}$ ( $m$ - масса тела), ${\displaystyle \bf v}_{{\displaystyle \bf 0}} \times {\displaystyle \bf p} = 0$ и ${\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf L}_{0} }}{\displaystyle {\displaystyle dt}}} = {\displaystyle \bf M}_{0} ,$ то есть уравнение моментов относительно движущегося центра масс имеет такой же вид, что и относительно неподвижной точки. Существенно отметить, что в этом случае, как было показано в конце лекции 2, скорости всех точек тела при определении $\bf L}_{0$ следует брать относительно центра масс тела.

Ранее было показано, что произвольное движение твердого тела можно разложить на поступательное (вместе с системой x₀y₀z₀, начало которой находится в некоторой точке - полюсе, жестко связанной с телом) и вращательное (вокруг мгновенной оси, проходящей через полюс). С точки зрения кинематики выбор полюса особого значения не имеет, с точки же зрения динамики полюс, как теперь понятно, удобно поместить в центр масс. Именно в этом случае уравнение моментов (3.2) может быть записано относительно центра масс (или оси, проходящей через центр масс) как относительно неподвижного начала (или неподвижное оси).

Если $\sum {\displaystyle {\displaystyle \bf F}}$ не зависит от угловой скорости тела, а $\sum {\displaystyle {\displaystyle \bf M}}$ - от скорости центра масс, то уравнения (3.1) и (3.2) можно рассматривать независимо друг от друга. В этом случае уравнение (3.1) соответствует просто задаче из механики точки, а уравнение (3.2) - задаче о вращении твердого тела вокруг неподвижной точки или неподвижной оси. Пример ситуации, когда уравнения (3.1) и (3.2) нельзя рассматривать независимо - движение вращающегося твердого тела в вязкой среде.

Далее в этой лекции мы рассмотрим уравнения динамики для трех частных случаев движения твердого тела: вращения вокруг неподвижной оси, плоского движения и, наконец, движения твердого тела, имеющего ось симметрии и закрепленного в центре масс.

Назад| Вперед

Публикации с ключевыми словами: механика - твердое тело - углы Эйлера Публикации со словами: механика - твердое тело - углы Эйлера
См. также: Механика сплошных сред Вариационные принципы механики Анизотропия

Мнения читателей [2]

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце