Астронет > Геофизические методы исследования земной коры. Часть 2

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Геофизические методы исследования земной коры

1.3. Принципы качественной и количественной интерпретации комплексных геофизических данных

1.3.1. Качественная интерпретация при комплексировании геофизических методов.

Качественная интерпретация сводится к выделению местоположения аномалообразующих объектов, объяснению их природы, выявлению аномалий, созданных одними и теми же источниками (например, рудные) или разными (например, рудные и нерудные). Выделение аномалий может проводиться визуально или статистическим способом с помощью ЭВМ. Сущность его основана на принципе аналогий, который состоит в перенесении на неизвестный участок подходов к анализу аномалий с эталонных, изученных участков сходного геологического строения или из " банка данных " [Тархов А.Г. и др., 1982].

Начинают качественную интерпретацию с выделения: аномалий разного знака (максимумов, минимумов), с разной степенью " изрезанности " , где чередуются небольшие знакопеременные аномалии с тем или иным пространственным периодом, нулевых (спокойных) значений и т.п. Закодировав их, например, в виде нормального ряда цифр 1, 2, 3, ... и подсчитав, сколько аномалий того или иного кода приходится на единицу изучаемой площади, можно с помощью ЭВМ провести картирование, сначала по одному ( $х$ ), а затем по комплексу ( $х, у, z, \ldots$ ) методов.

Для оценки связи между аномалиями того или иного вида (например, максимумов или минимумов) разных методов можно рассчитать по $n$ аномалиям коэффициент линейной корреляции ( $r _{ xy}$ ):
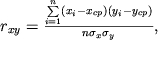$r_{xy}=\frac{\sum\limits_{i=1}^n\left( x_i - x_{cp}\right)\left(y_i - y_{cp}\right)}{n\sigma_x \sigma_y},$ (1.3)

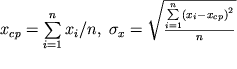где $x_{cp}=\sum\limits_{i=1}^n x_i/n,\; \sigma_x=\sqrt{\frac{\sum\limits_{i=1}^n \left( x_i - x_{cp}\right)^2}{n}}$ . Аналогичным образом рассчитываются значения $y_{ ср}$ и $\sigma _{ y }$ . При 0,7 $\lt |r _{ xy}| \lt$ 1 связи между разными физическими полями устойчивы и обусловлены одним и тем же источником. При $|r _{ xy}| \lt$ 0,5 можно говорить о слабых связях или об их отсутствии, что свидетельствует, например, о различной природе аномалий.

Заканчивают качественную интерпретацию анализом количественных признаков аномалий. Обычно это коэффициенты контрастности $\gamma _{ k}$ и $\gamma _{ э k}$ (1.1), где $k$ - номер метода. Надежное выделение аномалосоздающих объектов по комплексу методов ( $k$ = 1, 2, 3, ..., $М$ ) можно, например, получить с помощью функции комплексного показателя (ФКП):

$ФКП = \sum\limits_{k=1}^M C_k |\gamma_k|,$

(1.4)

где $M$ - число методов в комплексе, $| \gamma _{k} |$ - абсолютное значение коэффициента контрастности, $C _{ k}$ - логико-эвристический весовой коэффициент, вводимый интерпретатором на основе общих теоретических или практических представлений (например, при изучении массивной сульфидной залежи можно принять $С _{ сп}$ = 2, $С _{ вп}$ = 1,5, $С _{ кс}$ = 1 и т.д.). На картах и графиках ФПК максимумами выделяются положения эпицентров самых достоверных аномалосоздающих объектов.

Существуют и другие приемы выделения слабых аномалий: приемы распознавания образов, дискриминантный, кластерный, факторный и другие виды анализов. Сущность их сводится к изучению аномалий на этапах обучения и анализа. При обучении используются математические приемы оценки признаков аномалий над заведомо известными объектами, например, промышленными залежами руд. На этапе анализа эти признаки используются для обработки рядовых аномалий и распознавания искомых объектов. Алгоритмы разнообразных методов распознавания образов требуют большого объема вычислений с использованием ЭВМ.

1.3.2. Принципы количественной интерпретации комплексных геофизических данных.

Количественная интерпретация геофизических данных бывает пометодной и совместной, с использованием компьютеров или автоматизированных систем ( Кузне-цов О.Л., Никитин А.А., 1992).

1. Сущность пометодной и совместной комплексной интерпретации. Количественная интерпретация комплексных геофизических данных сводится к определению геометрических и геолого-гидрологических характеристик разведываемых объектов по совокупности решений обратных задач для разных методов. Наиболее простым является решение обратных задач для геофизических методов, описываемых сходными законами, например, для потенциальных методов геофизики (гравитационного, магнитного, естественного электрического поля). При решении обратных задач методом сравнения полевых кривых с расчетными постепенно изменяются геометрические и физические параметры разведываемых объектов до получения таких размеров, формы, глубины залегания и физических свойств, которые обеспечивают совпадения полевых и расчетных кривых.

Совместное решение обратных задач для нескольких методов реализуется путем использования способов многомерной статистики. Простейшим из них является получение уравнения многомерной регрессии. Для этого экспериментально, с помощью параметрических наблюдений, например, по скважинам и результатам петрофизических исследований, рассчитываются те или иные геолого-гидрологические и геометрические параметры, выражаемые численно ( $y _{ i}$ ). Это могут быть литология рыхлых осадочных пород, определяемая через средний диаметр твердых частиц ( $d _{ ср}$ ); коэффициенты содержания рудных минералов в породе ( $К _{ р}$ ), пористости ( $К _{ п}$ ), водонасыщенности ( $К _{ в}$ ), фильтрации ( $К _{ ф}$ ), водопроводимости ( $Т _{ в} = К _{ ср } \cdot h$ , где $h$ - мощность слоя); глубины залегания опорных горизонтов ( $Н$ ), например, кристаллического фундамента и др.

Для тех же объектов определяются геофизические параметры ( $х _{ i}$ ), получаемые наиболее точно, т.е. те, на которые принцип эквивалентности действует наименьшим образом. Например, $\Delta g _{ max }\cdot h / \Delta \sigma$ ( $\Delta g _{ max}$ - максимальная гравитационная аномалия от объекта с избыточной плотностью $\Delta \sigma$ , расположенного на глубине $h$ ); продольная электрическая проводимость слоя, подстилаемого высокоомной толщей ( $S _{ i} = h _{ i } / \rho _{ i}$ ); поперечное электрическое сопротивление слоя постоянному току ( $T _{ i} = h _{ i } \cdot \rho _{ i}$ ) или мощность ( $h _{ i}$ ) слоя при зондировании переменными полями, если он подстилается низкоомной толщей, и др. В ходе параметрических наблюдений (алгоритм обучения) используется формула многомерной линейной регрессии:

$y_{j} =a_{0} + \sum\limits_{i=1}^{n} a_{i} x_{i},$

(1.5)

где $a_{0} =y_{jcp} -\sum a_{i} x_{icp}, \; a_{i} =b_{i} \frac{\sigma_{yj} }{\sigma_{\xi } }$ . Здесь $y _{ j}$ - геологический параметр, определяемый по n геофизическим методам ( $x _{ 1} , x _{ 2}, \ldots, x _{ i}, \ldots, x _{ n}$ ), $a _{ 0}$ - свободный член, $a _{ i}$ - коэффициенты регрессии, значения $x _{ iср} , y _{ jср} , \sigma _{ xi} , \sigma _{ yj}$ рассчитываются по формуле (1.3), $b _{ i}$ - вспомогательные коэффициенты, получаемые при решении системы линейных уравнений множественной регрессии, ${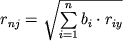r}_{nj} = \sqrt{\sum\limits_{i=1}^{n} {b}_{i} \cdot {r}_{iy}}$ - множественный коэффициент корреляции, $r _{ iy}$ - коэффициент парной корреляции между $y _{ j}$ и $x _{ i}$ (1.3).

В качестве примера можно привести полученное автором уравнение связи между процентным содержанием меди (Сu) на одном из пластовых месторождений медьсодержащих руд и параметрами вызванной ( $\eta$ ) и естественной ( $\alpha$ ) поляризации Cu = 1,46 + 0,35 $\eta$ - 0,04 $\alpha$ при $r$ = 0,83.

2. Автоматизированные системы комплексной интерпретации. Современные методы изучения недр основаны на использовании геологических, геохимических и разноуровневых (космических, воздушных, наземных, морских и скважинных) геофизических методов. В результате регистрируются огромные массивы информации, из которой реально обрабатывается не более 10%. Повышение эффективности и качества работ требует создания автоматизированных систем обработки (и интерпретации) данных (АСОД) на ЭВМ. Этим занимается новая отрасль геологии - геоинформатика. Разрабатываются АСОД, ориентированные на отдельные методы (грави-, магнито-, электро-, сейсморазведку, ядерную геофизику, ГИС), технологии (космические, аэрогеофизические, полевые, морские, скважинные), проблемы (поиски нефти и газа, рудных ископаемых, воды, решение задач инженерной геологии, гидрогеологии, геоэкологии и охраны окружающей среды), регионы (Русская платформа, Восточная и Западная Сибирь и др.). Любая из систем состоит из банка (базы) данных, системы управления и библиотеки обрабатывающих (прикладных) программ.

Более сложным этапом является создание интегрированных АСОД для комплексного геолого-геофизического проведения геолого-разведочных работ, совместной обработки и интерпретации материалов. Их основой станет не только база данных, но и база знаний как персональных (ПБЗ), так и обобщенных (ОБЗ). Ядром базы знаний являются данные опросов специалистов-экспертов, проводимых с целью разработки стратегии комплексных исследований недр. В результате будут создаваться автоматизированные и экспертные системы на основе тех или иных компьютерных технологий. Последние должны включать проектирование, проведение работ и комплексную интерпретацию.

1.4. Основы петрофизики

Ответственным, иногда самым трудным и неоднозначным по результатам этапом комплексных геофизических исследований является геолого-тектоническое, петрофизическое, гидрогеологическое, инженерно-геологическое, мерзлотно-гляциологическое и экологическое истолкование результатов. Оно выполняется с помощью петрофизических исследований [Вахромеев Г.С. и др., 1997].

Назад| Вперед

Публикации с ключевыми словами: геофизика - Земля - земная кора
Публикации со словами: геофизика - Земля - земная кора

См. также:

Земля из межпланетного пространства

Заход Земли с "Ориона"

Противосумеречные лучи и фестиваль планет

Восход Земли: видео

Ударный кратер Маникуаган: вид из космоса

Земля и Луна: вид с другой стороны

Снежная буря 1938 года в Верхнем Мичигане

Все публикации на ту же тему >>

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце