5. Диаграмма Герцшпрунга-Рессела
На космическом аппарате Hipparcos проводились измерения блеска звезд в двух
полосах ![]() ,
, ![]() в собственной фотометрической системе Tycho. Имеются
формулы для пересчета этих величин в стандартный показатель цвета B-V, но для
удобства эта величина уже внесена в каталог
в собственной фотометрической системе Tycho. Имеются
формулы для пересчета этих величин в стандартный показатель цвета B-V, но для
удобства эта величина уже внесена в каталог![]() Всего такая фотометрия была
сделана для 114 820 звезд в Hipparcos, кроме этого для 2117 звезд
фотометрические данные были взяты из наземных источников. Поле H39 (позиция
259) несет информацию об источнике B-V (символ G или T - наземные наблюдения
или Tycho). Для 115 180 звезд имеются данные и о спектральном классе.
Всего такая фотометрия была
сделана для 114 820 звезд в Hipparcos, кроме этого для 2117 звезд
фотометрические данные были взяты из наземных источников. Поле H39 (позиция
259) несет информацию об источнике B-V (символ G или T - наземные наблюдения
или Tycho). Для 115 180 звезд имеются данные и о спектральном классе.
Индивидуальные параллаксы позволяют вычислить абсолютную звездную величину или светимость для каждой звезды. Таким образом, имеется все необходимое для построения диаграммы Герцшпрунга-Рессела. Каталог Hipparcos дает уникальную возможность построить диаграмму для любой выборки звезд. До появления этого каталога это было невозможно из-за плохого знания расстояний. Диаграммы удавалось строить только для тех звезд, для которых имелась косвенная информация, что они находятся от нас примерно на одинаковом расстоянии, например, для звезд одного звездного скопления.
Следует заметить, что в программе Celestia вообще не предусмотрена работа с диаграммой Герцшпрунга-Рессела.
Алгоритм построения диаграммы достаточно прост и может быть легко дополнен программистом для решения более конкретных задач, связанных с использованием диаграммы Герцшпрунга-Рессела.
В начале программы определяются константы, описывающие охват прямоугольника
диаграммы, а также отступ рамки диаграммы от края графического окна и
максимальную относительную ошибку параллакса. Далее идет описание двух
глобальных переменных - масштабных множителей, которые используются в
процедуре XY, а вычисляются в главной программе. Процедура XY переводит
![]() и
и ![]() звезды в экранные координаты
звезды в экранные координаты ![]() ,
, ![]() .
.
Главная программа начинается с создания графического окна и определения
масштабных множителей в соответствии с разрешением экрана. Окно заливается
белым цветом, а цвет пера по умолчанию задается черным. Затем рисуется
обрамляющий прямоугольник диаграммы и происходит разметка осей штрихами в 3
пикселя и подписями с шагом 0.5![]() по
по ![]() и 5
и 5![]() по
по ![]() .
.
Листинг 5.1. Построение диаграммы Герцшпрунга-Рессела
Program HRBV; { Построение
HR-диаграммы }
Uses HipMain,Graph,Math;
const
MagLow =15.0; MagHi =-5.0; { Диапазон по абс.
зв. величине }
BVLow =-0.5; BVHi = 2.0; { Диапазон по
B-V }
Border = 50; { Отступ диаграммы от края
окна }
RelErr = 0.5; { Относительная точность
определения параллакса}
var { глоабальные
переменные }
ScaleMg : double; { Масштаб по оси абс. зв. величин }
ScaleBV : double; { Масштаб по оси показателя цвета }
{ Процедура пересчета B-V и M в экранные
координаты }
Procedure XY(B_V,Mag:single; var x,y :
integer);
begin
x:=Border+Round((B_V-BVLow)*ScaleBV);
y:=Border++Round((Mag-MagHi)*ScaleMg);
end;
var
driver, mode : smallint; { Для инициализации
графики }
s : THipparcos; { Звезда в Hipparcos
}
r : double; { Расстояние }
Mag : single; { Абсолютнаязвезднаявеличина
}
BV : single; { Показательцвета }
buf : string[15]; { Буфер для формирования
текстовых строк }
x,y,x1,y1 : integer; { Экранные
координаты }
color : integer; { Цвет точки }
begin
{ Инициализация графического окна
}
driver:=detect; mode:=0; InitGraph(driver,mode,'D:/BP/BGI');
{ Определение масштабов по осям }
ScaleMg:=(GetMaxY-2*Border)/(MagLow-MagHi);
ScaleBV:=(GetMaxY-2*Border)/(BVHi-BVLow);
{ Заливка фона и установка цвета }
SetFillStyle(SolidFill,White); Bar(0,0,GetMaxX,GetMaxY);
SetColor(Black);
{ Отрисовка обрамляющей рамки }
XY(BVLow,MagHi,x,y); XY(BVHi,MagLow,x1,y1);
Rectangle(x,y,x1,y1);
{ Разметка оси показателя цвета }
SetTextJustify(CenterText,TopText);
BV:=BVLow;
repeat
XY(BV,15,x,y); Line(x,y,x,y+3);
Str(BV:0:1,buf); OutTextXY(x,y+5,buf);
BV:=BV+0.5;
until BV>BVHi;
{ Разметка оси абс. зв. величин }
SetTextJustify(RightText,CenterText);
Mag:=MagHi;
Repeat
XY(BVLow,Mag,x,y); Line(x,y,x-3,y);
Str(Mag:0:0,buf); OutTextXY(x-5,y,buf);
Mag:=Mag+5;
until Mag>MagLow;
OpenHipparcosMain;
InitCriteria('100.txt');
while ReadHipparcosMain(s) do
begin
if (s.info and NoPlx)<>0
then continue; { нет
параллакса }
if (s.info and NoB_V)<>0
then continue; { нет
B-V }
if (s.info and NoVMag)<>0
then continue; { нет V
Mag }
if s.plx<=0.0 then continue; {
"плохой" параллакс }
if s.sigma.plx/s.plx>RelErr
then continue; { низкая
точность }
ifnot
inCelestia(s.HIP) then continue; {
нет в списке }
r:=1000.0/s.plx; { Вычисление расстояния в
пк }
Mag:=S.VMag-5.0*log10(r)+5.0; {Вычисл. абс.
звезд. величины}
case s.SP[0] of {
Определение цвета точки }
'O','B': color:=LightBlue;
'A' : color:=LightCyan;
'F','G': color:=Yellow;
'K','M': color:=LightRed;
else color:=LightGray;
end; { case }
XY(S.B_V,Mag,x,y); { Вычисление экранных
координат точки }
PutPixel(x,y,Color); { Поставить точку
}
end; { while }
ClearCriteria;
CloseHipparcosMain;
end.
Собственно цикл нанесения звезд на диаграмму является весьма простой процедурой. В начале тела цикла проверяется наличие у звезды всех необходимых для диаграммы Герцшпрунга-Рессела параметров. Затем проверяется присутствие звезды в списке, подготовленном программой Celestia. В нашем примере мы задали критерий отбора звезд c параллаксом больше 10 mas. Число таких звезд составило 22 982. Обращаем внимание, что при использовании 16-разрядных компиляторов список номеров звезд числом более 16 383 не поместится в 64К сегмент, следует использовать 32-разрядный компилятор или другой алгоритм проверки нахождения звезд в списке. Конечно, такой простой критерий несложно задать и непосредственно в программе оператором
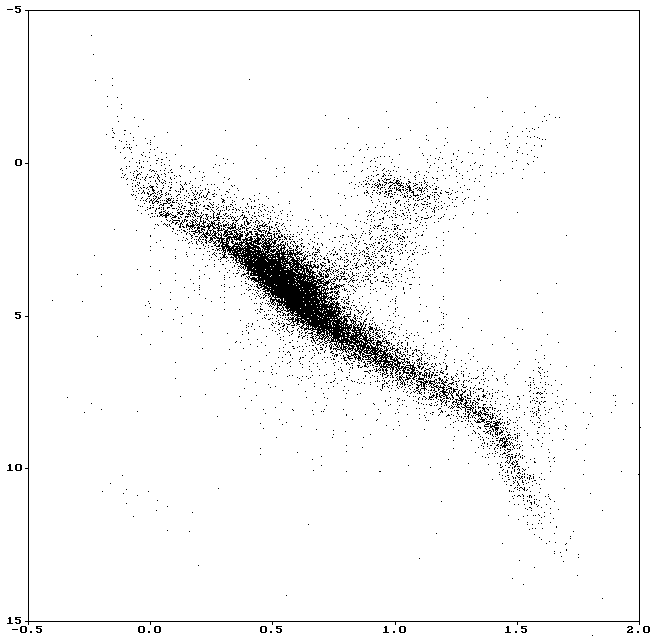
Рис. 5.1. Диаграмма Герцшпрунга-Рессела для звезд, находящихся на расстоянии ближе 100 пк. По оси абсцисс отложен показатель цвета B-V, по оси ординат - абсолютная звездная величина.
<< 4. Построение распределения звезд | Оглавление | 6. Упражнения >>
|
Публикации с ключевыми словами:
астрометрия - каталоги - Hipparcos
Публикации со словами: астрометрия - каталоги - Hipparcos | |
См. также:
Все публикации на ту же тему >> | |