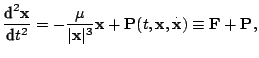<< 1. Введение | Оглавление | 3. Методы теории специальных ... >>
2. Трудности интегрирования классических уравнений
Уравнения орбитального движения в системе координат, связанной с массивным центральным телом, можно представить в виде
где
- вектор положения исследуемого тела;
- время; 
- гравитационный параметр;
-
кеплеровский член;
- возмущающие силы, причем
.
Интегрирование этих уравнений связано со следующими трудностями.
- Правые части уравнений (1) представляют собой большие и быстроизменяющиеся функции даже для круговых орбит. Как известно, вычисляемые на компьютере большие величины содержат большие ошибки округления. Поэтому пошаговое численное интегрирование классических уравнений будет сопряжено с быстрым накоплением ошибок округления.
- Уравнения
(1) имеют особенность в начале координат
(
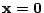). Для сильно эксцентричных эллиптических
орбит в перицентре, при сближении с центральным телом, величины
правых частей уравнений значительно и быстро возрастают. Поэтому
интегрирование орбиты вблизи перицентра выполняется с малым шагом
и большими ошибками.
- Уравнения (1)
неустойчивы по Ляпунову. Хорошо известно, что ляпуновская
неустойчивость дифференциальных уравнений при численном
интегрировании создает благоприятные
условия для усиления всевозможных ошибок, неизбежно сопровождающих любой численный процесс. Ошибки на текущем шаге интегрирования становятся ошибками начальных данных следующего, которые в дальнейшем усиливаются неустойчивостью шаг за шагом.
Предлагаемые в работе методы теории специальных возмущений полностью решают каждую из перечисленных проблем. Изложим общие идеи этих методов.
<< 1. Введение | Оглавление | 3. Методы теории специальных ... >>
|
Публикации с ключевыми словами:
Небесная механика
Публикации со словами: Небесная механика | |
См. также:
Все публикации на ту же тему >> | |
Астрометрия
-
Астрономические инструменты
-
Астрономическое образование
-
Астрофизика
-
История астрономии
-
Космонавтика, исследование космоса
-
Любительская астрономия
-
Планеты и Солнечная система
-
Солнце