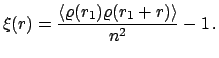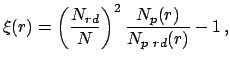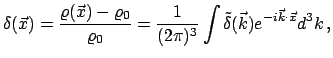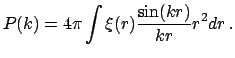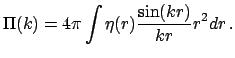<< 3. Способы описания структуры | Оглавление | 5. Современное состояние >>
4. Методы анализа структуры
На практике при изучении свойств крупномасштабной структуры процедура анализа каталогов оказывается достаточно сложной. Собственно анализу структуры должен предшествовать выбор определенной космологической модели, получение абсолютных величин галактик с учетом K-поправки, поглощения света, эффектов эволюции и пр., учет «геометрических» особенностей каталога (формы области, охваченной каталогом на небесной сфере и краевых эффектов), выделение достаточно полных по светимости выборок галактик, ограниченных по размеру. Только после этого можно приступать к выделению структуры.
Наиболее распространенным подходом к анализу крупномасштабной структуры Вселенной является метод корреляционных функций.
Корреляционная функция определяется как мера вероятности отклонения распределения частиц от пуассоновского однородного распределения на расстоянии ![]() от некоторой фиксированной частицы из данной выборки. Для определения двухточечной корреляционной функции
от некоторой фиксированной частицы из данной выборки. Для определения двухточечной корреляционной функции
![]() необходимо рассмотреть две бесконечно малые сферы в точках
необходимо рассмотреть две бесконечно малые сферы в точках ![]() и
и ![]() с объемами
с объемами ![]() и
и ![]() , тогда совместная вероятность найти одновременно объекты в сферах, расстояние между которыми равно
, тогда совместная вероятность найти одновременно объекты в сферах, расстояние между которыми равно ![]() , будет
, будет
где
Для получения оценки
где
Наиболее существенным предположением, лежащим в основе определения корреляционной функции, является условие априорного существования средней плотности числа объектов, которая не зависит от величины рассматриваемого объема. В частности, это предположение позволяет использовать бесконечно малые объемы в формуле (13).
Если пространственное распределение объектов характеризуется некоторой случайной функцией плотности, то флуктуации этой функции можно представить в виде интеграла Фурье как суперпозицию плоских пространственных волн
где Фурье-образ
Таким образом, полное описание пространственного распределения плотности объектов должно включать рассмотрение как спектра амплитуд
В случае гауссовых случайных процессов фазы плоских волн распределены равномерно в интервале
![]() и для характеристики поля плотности достаточно рассматривать только
спектр мощности
и для характеристики поля плотности достаточно рассматривать только
спектр мощности
В случае изотропных распределений спектр мощности и корреляционная функция связаны соотношением
Так что для степенной корреляционной функции
Большинство работ, посвященных анализу крупномасштабной структуры,
используют только спектр мощности ![]() , хотя фазовый спектр
несет в себе важную дополнительную информацию о негауссовости
процесса кластеризации объектов.
, хотя фазовый спектр
несет в себе важную дополнительную информацию о негауссовости
процесса кластеризации объектов.
Для стохастических фрактальных процессов также можно провести Фурье-анализ функции плотности. Можно ввести понятие масштабно независимого (обобщенного) спектра мощности фрактальных процессов ![]() , который определяется выражением, аналогичным (19), где вместо
, который определяется выражением, аналогичным (19), где вместо ![]() под интегралом стоит условная плотность
под интегралом стоит условная плотность ![]() (5), так что
(5), так что
В случае стохастических фрактальных процессов
Топология распределения представляет собой статистику, определяющую так называемый «род поверхности». Данная статистика проводится по сглаженному точечному распределению, которое получается при построении поверхностей одинаковой плотности. При этом исследуемый объем разделяется на области пониженной и повышенной плотности гладкими поверхностями.
Род ![]() поверхности определяется как
поверхности определяется как
| (20) |
где
Для сферы ![]() , для
, для ![]() изолированных сфер
изолированных сфер
![]() , для тора
, для тора ![]() . Вообще
. Вообще ![]() равен максимальному количеству принципиально различных разрезов поверхности, которые можно сделать, сохранив целостность тела.
равен максимальному количеству принципиально различных разрезов поверхности, которые можно сделать, сохранив целостность тела.
Минимальное охватывающее дерево - один из способов выявления кластеризации объектов. На объектах выборки строится граф (можно показать, что получающийся в результате граф единственен, поэтому начинать построение можно с любого объекта выборки). На некотором шаге происходит поиск объекта, находящегося на наименьшем расстоянии от какого-либо объекта, уже присоединенного к графу. Эти два объекта соединяются ребром. Далее процесс повторяется, пока все объекты выборки не будут присоединены к графу. После построения графа имеются данные о длинах ребер, соединяющих объекты, и о количестве ребер, присоединенных к каждой вершине графа. Используя эти данные, можно выделять объекты, находящиеся в областях повышенной и пониженной плотности.
Перколяция - один из методов кластерного анализа, используется для объединения областей повышенной плотности. Вокруг объекта, выбранного начальным, описывается сфера некоторого радиуса (перколяционный радиус - единственный задаваемый параметр этого метода). Если в сферу попадают объекты, вокруг них тоже описываются сферы того же радиуса, и так далее, пока ни в одну сферу не попадет ни один новый объект. Далее выбираются новые объекты, не вошедшие в кластеры, полученные ранее. Потом можно найти центры масс кластеров и отметить их как новые объекты. Таким образом, например, создавался известный каталог сверхскоплений Эйнасто.
Существуют также как многочисленные модификации перечисленных методов, так и менее распространенные статистики, используемые для изучения распределения астрофизических объектов. Например, более детальное построение трехмерной картины ближайших областей Вселенной послужило толчком к развитию разнообразных статистических методов выделения и исследования различных структур в распределении объектов во Вселенной - «пустот» (voids), «цепочек» (filaments), сверхскоплений («стен», состоящих из галактик). В отличие, например, от двухточечной корреляционной функции эти методы более тонко выделяют морфологические особенности структур.
<< 3. Способы описания структуры | Оглавление | 5. Современное состояние >>
|
Публикации с ключевыми словами:
крупномасштабная структура Вселенной
Публикации со словами: крупномасштабная структура Вселенной | |
См. также:
Все публикации на ту же тему >> | |