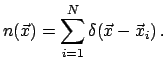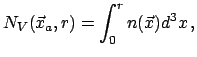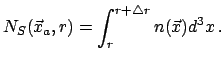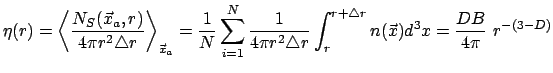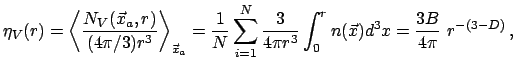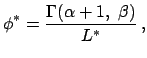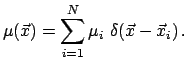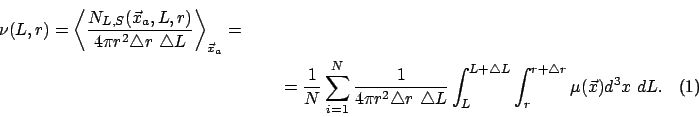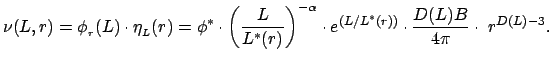<< 2. Наблюдательные данные | Оглавление | 4. Методы анализа структуры >>
3. Способы описания структуры
При описании крупномасштабной структуры сейчас, как правило, используется два типа моделей: однородная модель с флуктуациями плотности, а также фрактальная модель. Обе эти модели обладают как достоинствами, так и недостатками.
Однородное распределение, на которое накладываются флуктуации плотности конечной амплитуды, удобно для аналитического описания структуры. В то же время реально наблюдаемые особенности структуры - ее самоподобие в значительном интервале масштабов, отсутствие надежно выделяемых центров концентрации и т. п. - лучше описываются в рамках фрактальной модели. В последние годы фрактальные модели достаточно широко используются как в астрофизике, так и в физике вообще. Для многих систем фрактальные модели являются простейшими способами описания структуры, чем, в частности, объясняется их популярность. В то же время принципиальная неаналитичность фрактальных моделей создает значительные трудности при описании процессов, приводящих к формированию структур такого рода. Более подробно общие свойства фрактальных моделей рассматривались в лекции, прочитанной на XXXII Школе в 2003 г.
Понятие плотности жидкости/газа, обычно используемое в гидродинамике, содержит предположение о том, что существует значение плотности, не зависящее от величины элемента объема. Тогда можно определить плотность как функцию пространственных координат (как правило, непрерывную). В задаче анализа флуктуаций функция плотности может быть реализацией стохастического процесса, для которого определены обычные моменты - среднее, дисперсия и т. д. В частности, это может быть и дискретный процесс, содержащий конечное число точек, например, пуассоновский процесс.
В случае фрактальных структур понятия плотности числа частиц в
точке не существует, так как в каждом элементе объема структуры
содержится иерархия кластеров и значение концентрации существенно
зависит от величины элемента объема. Для описания непрерывной
иерархии скучивания, являющейся новой характеристикой процесса,
необходимо ввести специальную независимую переменную - радиус
области (![]() ), в которой производится подсчет частиц. При этом
число частиц самоподобной структуры растет по степенному закону
), в которой производится подсчет частиц. При этом
число частиц самоподобной структуры растет по степенному закону
где
Рассмотрим дискретный стохастический процесс, реализации которого
представляют совокупности частиц, расположенных в случайно
выпавших положениях
![]() , так что
реализованная плотность числа частиц
, так что
реализованная плотность числа частиц
![]() дается
выражением
дается
выражением
Если стохастический процесс является фрактальным, то для его описания необходимо рассмотреть дополнительную «фрактальную» переменную
и
При переходе от реализации к реализации эти величины испытывают
флуктуации, после осреднения которых по множеству реализаций
остается зависимость от масштаба ![]() . В случае эргодических
процессов осреднение по реализациям можно заменить осреднением по
множеству точек одной реализации. Определим условную концентрацию
стохастического фрактального процесса в виде
. В случае эргодических
процессов осреднение по реализациям можно заменить осреднением по
множеству точек одной реализации. Определим условную концентрацию
стохастического фрактального процесса в виде
и объемную условную концентрацию в виде
где
называется фрактальной коразмерностью структуры.
Принципиально важным свойством условной концентрации является то,
что для процессов с конечным масштабом фрактальности, после
которого распределение частиц становится однородным, статистики
(5) и (6) выходят на постоянное значение,
что соответствует равенству ![]() для однородных структур. Таким
образом, метод условной концентрации является мощным инструментом
поиска границы перехода от режима фрактальной кластеризации к
однородности.
для однородных структур. Таким
образом, метод условной концентрации является мощным инструментом
поиска границы перехода от режима фрактальной кластеризации к
однородности.
Выше мы рассмотрели фрактальные стохастические процессы для частиц
одного сорта. Реальные галактики имеют функцию светимости ![]() , обычно задаваемую законом Шехтера
, обычно задаваемую законом Шехтера
описывающим долю галактик со светимостями в интервале
где
Стохастические процессы, в которых фрактальные носители (положения
частиц) характеризуются различными значениями некоторой случайной
величины ![]() (например, светимости
(например, светимости ![]() или массы
или массы ![]() ), относятся
к классу мультифрактальных процессов. Рассмотрим реализацию такого
стохастического процесса, которая характеризуется следующей
реализованной плотностью светимости (массы):
), относятся
к классу мультифрактальных процессов. Рассмотрим реализацию такого
стохастического процесса, которая характеризуется следующей
реализованной плотностью светимости (массы):
В таком случае функция плотности (светимости, массы) галактик является мультифрактальной мерой на множестве реализаций. Мультифракталы характеризуются спектром фрактальных размерностей
Пусть
![]() - число галактик со
светимостями в интервале
- число галактик со
светимостями в интервале
![]() в сферической
оболочке
в сферической
оболочке
![]() с центром в точке
с центром в точке
![]() , принадлежащей структуре. Обобщая понятие условной
концентрации (5) одинаковых частиц на случай частиц,
характеризующихся разными значениями светимости (массы), введем
условную плотность светимости (массы) галактик в виде
, принадлежащей структуре. Обобщая понятие условной
концентрации (5) одинаковых частиц на случай частиц,
характеризующихся разными значениями светимости (массы), введем
условную плотность светимости (массы) галактик в виде
Можно показать, что для широкого класса мультифрактальных стохастических процессов условную плотность светимости можно представить в виде
При этом шехтеровский вид функции светимости получается как следствие мультифрактальности, а не как дополнительное предположение. Особенностью выражения (12) является зависимость параметра излома функции светимости от радиуса области
<< 2. Наблюдательные данные | Оглавление | 4. Методы анализа структуры >>
|
Публикации с ключевыми словами:
крупномасштабная структура Вселенной
Публикации со словами: крупномасштабная структура Вселенной | |
См. также:
Все публикации на ту же тему >> | |