Лекция 10. Вращение Галактики
10.5 Кривая вращения Галактики
Получение кривой вращения Галактики - главная цель кинематических исследований Галактики. Она интересна не только сама по себе как функция, описывающая кинематические свойства Галактики. Она, прежде всего, важна тем, что содержит информацию о распределении материи в Галактике. Действительно, круговая скорость может быть определена из равенства силы тяготения центростремительной силе, удерживающей тело на круговой орбите:
Какой может быть кривая вращения нашей Галактики? Можно рассмотреть два предельных случая. Первый - это твердотельное вращение, когда при любом расстоянии от центра Галактики R угловая скорость вращения одинакова, а линейная скорость возрастает пропорционально R. Второй - это кеплеровское вращение, когда вся масса Галактики сосредоточена в ее центре. В этом случае мы имеем убывающую кривую линейных скоростей, пропорциональную R-1/2.
Перейдем теперь к способам определения кривой вращения из наблюдательных данных. Вновь обратимся к формуле Ботлингера для лучевых скоростей:
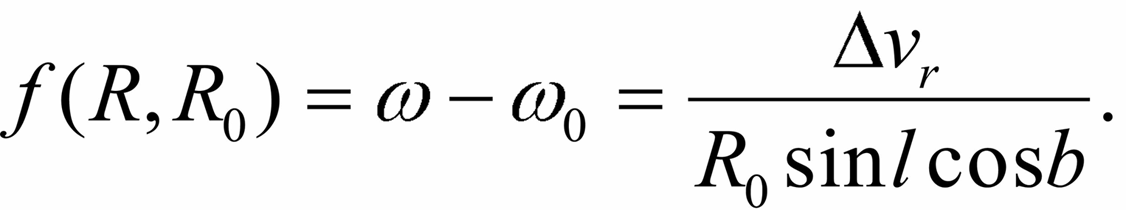
|
Применение метода Камма можно разбить на следующие этапы:
- - определение для избранной группы объектов индивидуальных расстояний r, исправленных за межзвездное поглощение;
- - вычисление расстояния от оси вращения Галактики R для каждого из объектов по теореме косинусов:
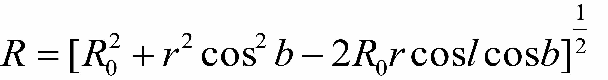
- - определение ω - ω0 для каждого из объектов;
- - если объектов в выборке много, то - усреднение функции Камма в подходящих интервалах R и построение графика как функции R.
Отметим попутно, что подходящим образом сглаженная функция Камма может служить для определения постоянной Оорта А путем численного дифференцирования, что является более обоснованным методом получения оценки постоянной Оорта, так как оценивание по формуле (10-13) позволяет определить эту величину лишь как коэффициент приближающего наблюдаемое поле скоростей полинома.
В § 10.4 было показано, как по наблюдательным данным можно оценить частоту вращения Галактики на круге Солнца . Если добавить к функции Камма эту величину, а затем каждую точку умножить на соответствующее значение R, мы получим кривую дифференциального вращения Галактики в виде кривой линейных скоростей вращения. Кривая линейных скоростей гораздо более наглядна и удобна для исследования. На рис.10-3 сведены результаты исследований последних лет, где кривая вращения определена по самым разным объектам - по радиоизлучению нейтрального водорода и молекулярных облаков, по лучевым скоростям рассеянных скоплений и классических цефеид и т.д. В качестве ординаты использовано галактоцентрическое расстояние в единицах расстояния Солнца от центра Галактики R0. Как можно видеть из рисунка, кривая вращения нашей Галактики более-менее надежно определена до галактоцентрического расстояния примерно 12 кпк (нами принято R0 = 8 кпк). Что делается за этим пределом не вполне ясно, однако, похоже, что максимум кривой вращения пока не достигается. Впрочем, в этой области очень велики ошибки определения кривой вращения и для уверенных выводов требуются дальнейшие исследования.
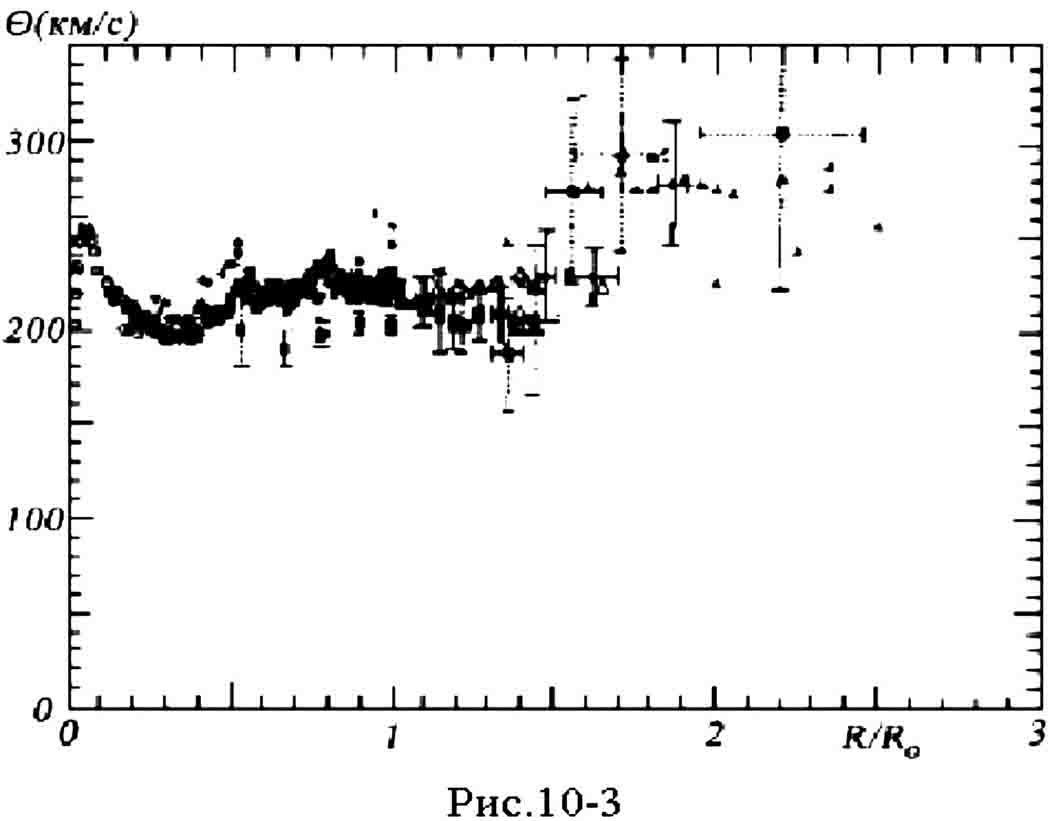 Характерными особенностями кривой вращения, выделяющимися на рис. 10-3, являются резкий минимум вблизи галактического центра, острый максимум на расстоянии около 1 кпк от центра, затем вторичный минимум и вновь небольшой максимум, после которого наблюдается небольшое убывание в окрестности солнечного радиуса орбиты и, как минимум, отсутствие убывания на периферии Галактики. Такое сложное поведение кривой вращения
определяется сложным распределением масс в Галактике, а также тем фактом, что Галактика, как мы знаем из предыдущих параграфов, состоит из подсистем с разными кинематическими свойствами. Очевидно, что на большом расстоянии от центра Галактики кривая вращения должна иметь кеплеровский убывающий характер, однако наблюдения показывают, что там, где есть наблюдаемое светящееся вещество, кривая вращения возможно даже не достигает максимума.
Характерными особенностями кривой вращения, выделяющимися на рис. 10-3, являются резкий минимум вблизи галактического центра, острый максимум на расстоянии около 1 кпк от центра, затем вторичный минимум и вновь небольшой максимум, после которого наблюдается небольшое убывание в окрестности солнечного радиуса орбиты и, как минимум, отсутствие убывания на периферии Галактики. Такое сложное поведение кривой вращения
определяется сложным распределением масс в Галактике, а также тем фактом, что Галактика, как мы знаем из предыдущих параграфов, состоит из подсистем с разными кинематическими свойствами. Очевидно, что на большом расстоянии от центра Галактики кривая вращения должна иметь кеплеровский убывающий характер, однако наблюдения показывают, что там, где есть наблюдаемое светящееся вещество, кривая вращения возможно даже не достигает максимума.
Кривая вращения, совместно с другими данными, дает возможность построить модель распределения масс в Галактике. Этот вопрос будет рассмотрен в 15-й лекции.
|
Публикации с ключевыми словами:
звездная астрономия
Публикации со словами: звездная астрономия | |
См. также:
Все публикации на ту же тему >> | |