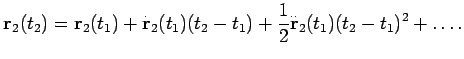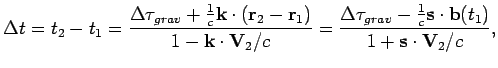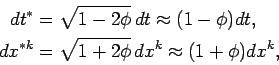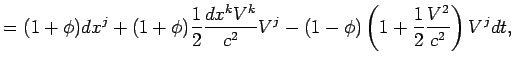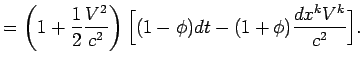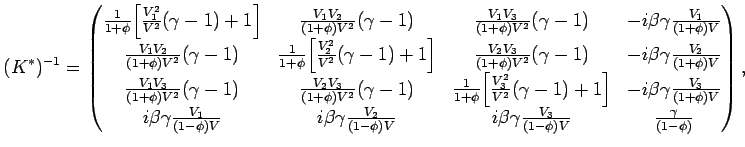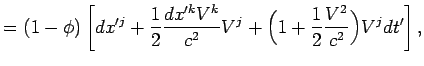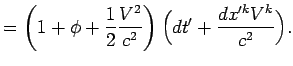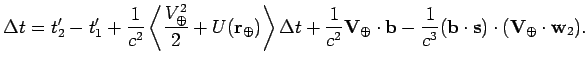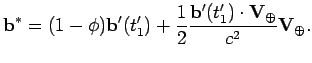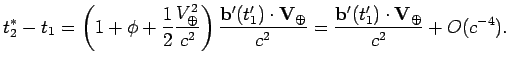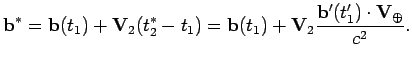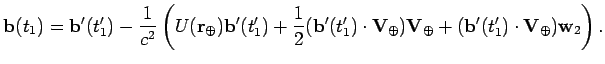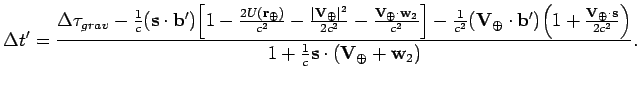<< 8.2. Вычисление гравитационной задержки
| Оглавление |
8.4. Вычисление частных производных >>
8.3. Вычисление геометрической задержки
Для вычисления геометрической задержки будем считать, что радиоисточник находится на бесконечно большом расстоянии от наблюдателя, т.е. фронт приходящей волны - плоский. Найдем сначала выражение для задержки в барицентрической системе отсчета (пункт 5, см.§ 8.1), используя уравнение (8.3).
Так как вычисления задержки должны выполняться для момента
времени прихода фронта волны на телескоп 1, т.е. 
, то
разложим вектор
в ряд:
Для телескопов, расположенных на Земле, скорость
км/с, ускорение
. Для максимальной базы, реализуемой на
Земле (
км), задержка 
равна 
с.
Значит вклад второго члена в длину вектора 
равен
км, третьего - менее 
мм. Отсюда делаем вывод,
что по сравнению с точностью вычислений (0,3 мм) вкладом
ускорения можно пренебречь.
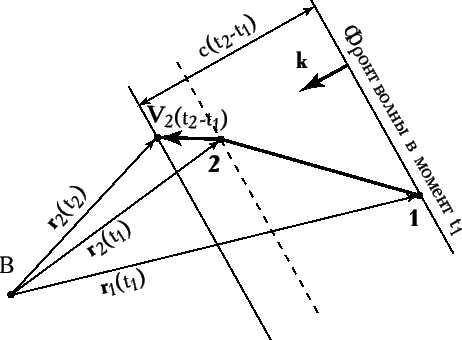
В момент прихода плоского фронта волны на телескоп 1 его
радиус-вектор относительно барицентра 
солнечной системы равен
, где - время TCB. В момент времени
радиус-вектор телескопа 2 в этой же системе равен
и в момент прихода фронта волны -
(рис. 8.2).
Пусть скорость второй антенны равна
.
Тогда, используя уравнения (8.3) и (8.9), найдем
где
- единичный вектор в направлении распространения
волны. Если 
- единичный барицентрический вектор
источника, то
. Из (8.10) получим:
. Все вектора
в (8.11) вычисляются в барицентрической системе отсчета на
момент времени . Скорость второго пункта может быть
представлена в виде суммы двух векторов: барицентрической
скорости геоцентра
и линейной скорости
, определяемой вращением
Земли, т.е.
.
На этапе редукции (пункт 6, см.§ 8.1) задержку (8.11) необходимо пересчитать в геоцентрическую небесную систему. Для этого используем преобразования Лоренца, записанные в виде (6.96-6.97), и исправим их для учета гравитационного поля Солнечной системы в центре Земли.
Для этого воспользуемся выражением (5.37) для интервала, которое запишем в следующем виде:
где
, 
- гравитационный потенциал всех тел
солнечной системы в точке расположения часов. В
уравнении (8.12) использовано правило суммирования Эйнштейна.
Если ввести новую систему координат
такую,
что
то интервал записывается в виде:
метрика является
метрикой Минковского, и законы физики могут быть записаны в
рамках специальной теории относительности. Координаты, помеченные
звездочкой, определены в барицентрической системе отсчета. Чтобы
найти соответствующие координаты и промежутки времени в системе,
связанной с движущейся Землей, и которые по-прежнему будем
отмечать штрихами, необходимо выполнить преобразования
Лоренца (6.96-6.97). Запишем их в дифференциальной форме:
 |
 |
|
 |
 |
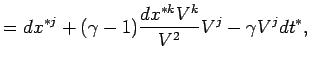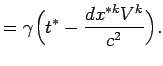Если ограничиться членами порядка 
, то
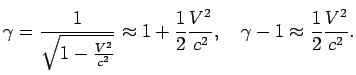
Обратное преобразование легко найти с помощью матричного метода. Для этого необходимо записать уравнения (8.14-8.15) в матричном виде, т.е. определить матрицу
, аналогичную матрице
(6.93), и вычислить обратную матрицу:
где
,
- барицентрическая скорость центра
масс Земли. Из (8.16) следует, что дифференциальное
преобразование координат и промежутков времени из движущейся
(штрихованной) системы к барицентрической системе записывается в
виде:
Если часы находятся в покое относительно Земли, то 
.
Следовательно, соотношение между промежутками координатного и
собственного времени из (8.18) имеет известный нам вид:
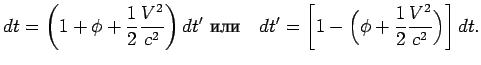
Согласно соглашению мы должны вычислять все величины на момент
времени . Поэтому из (8.18) имеем:
. В результате получим:
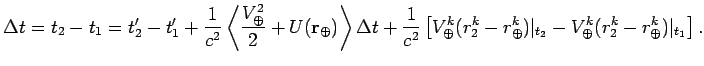
Расстояние между двумя точками в земной системе отсчета
определяется выражением (8.17) при 
и может быть
найдено интегрированием. Пренебрегая вариациями потенциала и
изменением скорости этих точек (такие вариации малы по сравнению
с потенциалом на поверхности Земли и средней скоростью), получим:
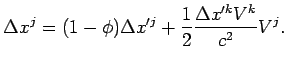
Расстояние между двумя точками (вектор базы
) в момент
собственного времени 
соответствует вектору
в
барицентрической системе, причем:
Чтобы выразить вектор
через
, заметим, что два события,
одновременных в геоцентрической системе координат и произошедших
в момент , разделены промежутком координатного
времени (8.18):
Учитывая, что в барицентрической системе отсчета
:
Пренебрегая членами порядка 
и выше из уравнений (8.20)
и (8.22), получим (пункт 4, см.§ 8.1):
Выразим теперь левую часть формулы (8.11) через разность
, т.е. заменим 
по
формуле (8.19), а вектор
на
согласно (8.23). После приведения подобных членов получим
окончательную формулу для задержки сигнала в геоцентрической
системе координат (пункт 6, см.§ 8.1):
Расчетная задержка 
получается путем добавления к 
задержки в тропосфере и ионосфере, а также поправки за
рассинхронизацию часов:
вычисляются для телескопов 1 и 2 по
формуле (6.55), а ионосферная задержка
находится очень точно, если
наблюдения велись одновременно на двух частотах (6.37).
Основной вклад в ошибку вычисления вносит неточность
вычисления задержки в тропосфере, вызванной наличием водяного
пара в тропосфере.
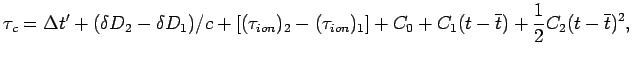
Обычно поправка за рассинхронизацию часов представляется в виде
квадратичного полинома, коэффициенты
которого
уточняются при решении системы условных уравнений (8.4); 
- момент наблюдения в шкале UTC,
- средний
момент.
<< 8.2. Вычисление гравитационной задержки | Оглавление | 8.4. Вычисление частных производных >>
|
Публикации с ключевыми словами:
астрометрия - сферическая астрономия - системы координат - шкалы времени
Публикации со словами: астрометрия - сферическая астрономия - системы координат - шкалы времени | |
См. также:
Все публикации на ту же тему >> | |
