8. Редукция наблюдений на РСДБ
Разделы
- 8.1. Основные этапы редукции наблюдений на РСДБ
- 8.2. Вычисление гравитационной задержки
- 8.3. Вычисление геометрической задержки
- 8.4. Вычисление частных производных по нутации в долготе и нутации в наклоне
Одним из современных астрометрических методов наблюдений является
радиоинтерферометрия со сверхдлинными базами (РСДБ). Два
радиотелескопа, находящиеся на большом расстоянии друг от друга,
одновременно наблюдают радиоисточник на частоте
![]() .
База (расстояние между телескопами) может быть от нескольких км
до нескольких тысяч км. Если обозначить один из телескопов
первым, а другой - вторым, то вектор
.
База (расстояние между телескопами) может быть от нескольких км
до нескольких тысяч км. Если обозначить один из телескопов
первым, а другой - вторым, то вектор ![]() (рис. 6.5), равный
(рис. 6.5), равный
![]() ,
называется вектором базы, где
,
называется вектором базы, где
![]() -
радиус-векторы телескопов.
Если вектор
-
радиус-векторы телескопов.
Если вектор ![]() известен точно, а
известен точно, а ![]() - единичный
вектор в направлении наблюдаемого источника с известными
координатами, то
- единичный
вектор в направлении наблюдаемого источника с известными
координатами, то
где
Каждый пункт РСДБ оснащен стандартом частоты, системой приема и преобразования высокочастотного радиосигнала к низкочастотному сигналу (к видеополосе) и системой регистрации. По заранее составленной программе телескопы (как правило, это параболические антенны) одновременно наблюдают в течение нескольких минут один и тот же радиоисточник. Так как принимаемые радиосигналы являются шумовыми сигналами малой мощности, то сначала они усиливаются, затем преобразуются в низкочастотную область спектра и, наконец, преобразуются из аналогового в цифровой вид. Цифровой сигнал, представляющий из себя случайную последовательность единиц и нулей, на каждом пункте записывается на магнитную ленту вместе с метками времени от стандарта частоты. Затем, следуя программе наблюдений, антенны переводятся на следующий источник, и цикл повторяется.
При проведении астрометрических наблюдений в сеансе участвуют от 3 до 10 антенн. В среднем один сеанс длится одни сутки. За это время на каждой станции выполняется 100 - 200 наблюдений 10 - 20 радиоисточников.
После завершения наблюдений магнитные ленты с каждого пункта РСДБ
перевозятся в центр обработки, где выполняется корреляционный
анализ: вычисляется амплитуда и фаза ![]() взаимной
корреляционной функции сигналов для каждой пары антенн. В
идеальном случае последовательность единиц и нулей между одними и
теми же метками времени на разных магнитных лентах должна быть
одинаковой. В этом случае амплитуда корреляционной функции
равнялась бы единице, а фаза зависела бы лишь от задержки
сигнала8.1. В реальной ситуации амплитуда
очень мала (порядка
взаимной
корреляционной функции сигналов для каждой пары антенн. В
идеальном случае последовательность единиц и нулей между одними и
теми же метками времени на разных магнитных лентах должна быть
одинаковой. В этом случае амплитуда корреляционной функции
равнялась бы единице, а фаза зависела бы лишь от задержки
сигнала8.1. В реальной ситуации амплитуда
очень мала (порядка ![]() для мощных радиоисточников), и
в дальнейшей обработке не используется (хотя есть смысл
определять веса наблюдений в зависимости от амплитуды).
для мощных радиоисточников), и
в дальнейшей обработке не используется (хотя есть смысл
определять веса наблюдений в зависимости от амплитуды).
В результате обработки лент определяется групповая временная
задержка сигнала и частота интерференции, которые равны
производной фазы ![]() кросскорреляционного сигнала по
отношению к циклической частоте наблюдений
кросскорреляционного сигнала по
отношению к циклической частоте наблюдений ![]() и скорости
изменения фазы, соответственно:
и скорости
изменения фазы, соответственно:
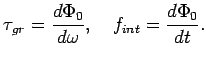
Если бы координаты телескопов и источника были известны точно,
отсутствовала бы атмосфера, часы были бы синхронизованы точно, то
групповая задержка ![]() равнялась бы геометрической
задержке
равнялась бы геометрической
задержке ![]() (8.1):
(8.1):
![]() . В
действительности уравнение (8.1) имеет вид:
. В
действительности уравнение (8.1) имеет вид:
где поправка
Расчетная задержка зависит от десятков параметров. Поэтому на следующем этапе обработки РСДБ наблюдений в зависимости от задачи выбирают те параметры, которые следует уточнить. После этого строится матрица условных уравнений относительно уточняемых параметров. Решение системы завершает обработку наблюдений.
Таким образом на первом этапе необходимо с максимально возможной точностью вычислить расчетные задержку и частоту интерференции для каждого наблюдения на основе принятой модели вращения Земли и движения ее по орбите, приливного и неприливного смещения телескопов, теории прецессии и нутации и т.д. В настоящее время модель вычисления задержки и частоты интерференции определена стандартами Международной службы вращения Земли.
В соответствии со стандартами МСВЗ модель задержки вычисляется в рамках общей теории относительности, используя определения барицентрической и геоцентрической систем отсчета (BCRS и GCRS).
В системе BCRS задержка записывается в виде:
где
Уравнение (8.3) преобразуется в уравнение для геоцентрической
задержки. Для этого используются формулы релятивистского
преобразования барицентрических векторов
![]() в
соответствующие геоцентрические векторы
в
соответствующие геоцентрические векторы
![]() и промежутка времени
и промежутка времени ![]() (TCB) в промежуток времени TCG:
(TCB) в промежуток времени TCG:
![]() . Решая эти два уравнения,
можно выразить геоцентрическую задержку через геоцентрический
вектор базы
. Решая эти два уравнения,
можно выразить геоцентрическую задержку через геоцентрический
вектор базы
![]() .
.
Это решение определяет задержку в шкале TCG, которая является шкалой координатного времени в системе GCRS. Векторы также выражаются в системе GCRS.
Однако метки времени, записываемые на магнитные ленты и
используемые при корреляции сигналов, формируются стандартами
частоты, которые, как мы знаем, отражают собственное время. В
действительности перед началом наблюдений стандарты на всех
телескопах, участвующих в сеансе РСДБ, синхронизируются между
собой с помощью радио, телесигналов в шкале UTC с максимально
возможной точностью. Поэтому можно считать, что измеренная
задержка выражается не в собственном времени часов, а в шкале
координатного времени TT (так как шкала TT отличается от шкалы
UTC только смещением). Тогда в формуле для задержки ![]() (TT) вектор базы
(TT) вектор базы
![]() выражается не в GCRS, а в другой
системе: пространственные координаты, получаемые из анализа
данных РСДБ, согласованы со шкалой TT, а не TCG.
выражается не в GCRS, а в другой
системе: пространственные координаты, получаемые из анализа
данных РСДБ, согласованы со шкалой TT, а не TCG.
Именно этот алгоритм используется во всех центрах анализа наблюдений на РСДБ. Координаты телескопов, следовательно, приводятся не в системе GCRS; масштаб земной системы координат ITRF2000 не удовлетворяет резолюциям МАС (см. также стр. ).
После того как разработана модель задержки, можно найти расчетные
значения задержки и частоты интерференции (обозначим их как
![]() и
и ![]() ), которые равны геометрическим значениям плюс
поправки за атмосферу и рассинхронизацию часов. Одновременно
вычисляются частные производные задержки и частоты интерференции
по параметрам модели.
), которые равны геометрическим значениям плюс
поправки за атмосферу и рассинхронизацию часов. Одновременно
вычисляются частные производные задержки и частоты интерференции
по параметрам модели.
Этот этап в соответствии с традициями астрометрии можно назвать редукцией РСДБ-наблюдений.
Современная точность измерения групповой задержки составляет в
среднем
![]() с или 10 пкс, а частоты интерференции -
с или 10 пкс, а частоты интерференции -
![]() с/с. Поэтому точность вычисления задержки
(точность модели наблюдений) должна быть не хуже 1 пкс (в
линейной мере
с/с. Поэтому точность вычисления задержки
(точность модели наблюдений) должна быть не хуже 1 пкс (в
линейной мере ![]() мм).
мм).
На втором этапе обработки для каждого наблюдения разность
измеренной и вычисленной задержки (частоты интерференции)
представляется в виде разложения по малым параметрам -
поправкам к принятым значениям параметров ![]() модели:
модели:
причем число параметров
На третьем этапе выполняется оценивание параметров
модели. Чаще всего для этого используется метод наименьших
квадратов. Решение системы условных уравнений (8.4) дает
поправки
![]() к параметрам, которые нас интересуют.
к параметрам, которые нас интересуют.
<< 7.5. Преобразование из земной | Оглавление | 8.1. Основные этапы редукции >>
|
Публикации с ключевыми словами:
астрометрия - сферическая астрономия - системы координат - шкалы времени
Публикации со словами: астрометрия - сферическая астрономия - системы координат - шкалы времени | |
См. также:
Все публикации на ту же тему >> | |