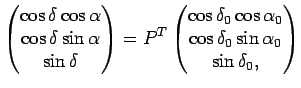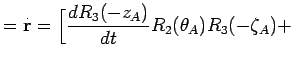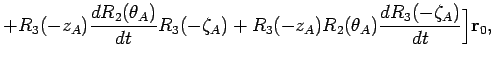Астронет | Картинка дня | Обзоры astro-ph | Новости | Статьи | Книги | Карта неба | Созвездия | Переменные Звезды | Глоссарий

Физика космоса | Биографии | Словарь | Ключевые слова | Астрономия в России | Форумы | Семинары | Сверхновые

<< 7.1. Причины прецессии и | Оглавление | 7.3. Математическое описание прецессии >>

7.2. Определение матрицы прецессии

Явление лунно-солнечной прецессии заключается в повороте плоскости экватора относительно плоскости эклиптики. Если с плоскостью экватора связана система координат, то это означает, что прецессия приводит к вращению системы координат относительно инерциального пространства. Чтобы учесть влияние прецессии на координаты звезд, используем матричный метод.

Пусть положение экваториальной системы координат с началом в точке в эпоху определяется полюсом мира и плоскостью экватора, которая задается осями . Эпоха часто совпадает с одной из фундаментальных эпох (например, J2000.0). Ось направлена в точку весеннего равноденствия . В результате прецессии экватор поворачивается и в эпоху займет другое положение, определяемое полюсом и точкой весеннего равноденствия , в которую направлена ось (рис. 7.6).

Положение системы относительно определяется с помощью трех углов Эйлера, которые в обозначениях Ньюкомба имеют вид: . Согласно определению Ньюкомба дуга равна , ; угол равен углу между плоскостями экваторов. Очевидно, что дуга равна прямому восхождению восходящего узла экватора эпохи на экваторе эпохи : . Соответственно дуга равна прямому восхождению точки , отсчитываемому от точки : .

Как уже говорилось, по соглашению системы координат, изменяющие свое положение только из-за прецессии, называются средними. Следовательно, системы координат , являются средними на эпохи и . Матричное уравнение

определяет преобразование координат единичного вектора из средней системы в эпоху к координатам единичного вектора в эпоху . Матрица называется матрицей прецессии и определяет поворот средней системы за счет прецессии за промежуток времени . Матрица является ортогональной. Поэтому обратное преобразование от средней системы в эпоху к средней системе в эпоху легко найти, заменив на транспонированную матрицу :

Явное выражение матрицы прецессии легко найти, воспользовавшись матрицами вращений (3.15). Три правых поворота: первый - относительно оси на угол , второй - относительно линии узлов, с которой совмещается ось , на угол и третий -относительно оси на угол переводят систему в . Таким образом матрица преобразования координат вектора, заданных на эпоху , к координатам на эпоху равна

Обратное преобразование координат от эпохи на эпоху определяется матрицей :

Следовательно, при переходе от эпохи к эпохе экваториальные координаты преобразуются по матричному уравнению:

где координаты звезды относятся к экватору эпохи , а - к экватору эпохи .

Численные выражения прецессионных величин были найдены Ньюкомбом частично на основе теории прецессии, частично из наблюдений, в виде разложений по двум параметрам: и , причем и равны числу юлианских столетий от начальной эпохи до фундаментальной эпохи J2000.0 и произвольной эпохи от . Если начальная эпоха совпадает с эпохой J2000.0 (при этом ), разложения принимают более простой вид

где - прецессии по прямому восхождению и склонению для эпохи J2000.0.

Подставляя вместо полученные выше значения, находим разложения для прецессионных величин :

Международный астрономический союз рекомендовал использовать разложения (7.5-7.7) и (7.20), начиная с 1984 г. Поэтому приведенные уравнения(7.5-7.7) и (7.20) следует использовать для вычисления матрицы прецессии, начиная с 1984 г.

Матричное уравнение (7.18) является точным, но его решение требует значительных усилий. Для приближенных вычислений раньше использовались более простые формулы. Допустим, что звезда на эпоху имеет экваториальные координаты и эклиптические координаты , а на эпоху - и , соответственно. Если предположить, что за короткий промежуток времени между двумя эпохами и положение эклиптики не меняется, то, очевидно, эклиптическая широта звезды не меняется. Так как точка весеннего равноденствия смещается из-за прецессии к западу (см. рис. 7.5), то эклиптическая долгота звезды увеличится на величину , если разница эпох измеряется в годах. Таким образом изменение эклиптических координат из-за лунно-солнечной прецессии равно:

Чтобы найти изменение экваториальных координат, воспользуемся уравнением (3.11):

Предположим, что за промежуток времени наклон эклиптики к экватору не меняется, т.е. (рис. 7.5). Тогда изменение склонения связано с изменением эклиптической долготы посредством уравнения:

Воспользовавшись уравнением (3.9)

найдем, что изменение склонения равно:

Дифференцируя (3.9), получим

или, после подстановки и :

Исключить эклиптические координаты можно, используя формулу подобия (3.14). После преобразований получим, что изменение прямого восхождения звезды равно:

Таким образом, если звезда находится достаточно далеко от полюса мира и интервал времени мал (порядка года или меньше), то для перевода экваториальных координат от эпохи к эпохе можно использовать формулы:

Правые части вычисляются итерациями: на первом шаге полагают и определяют . Результатом первой итерации являются полусуммы: , . Значения , подставляют в правые части уравнений и выполняют вторую итерацию, и т.д., пока результаты -ой итерации , не будут отличаться от , на некоторую малую заданную величину.

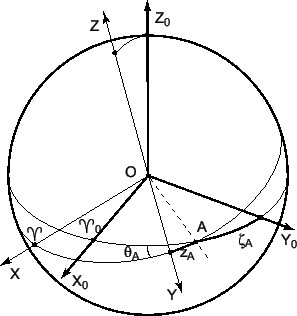
Рассмотрим теперь вопрос влияния прецессии на скорость изменения экваториальных координат. Продифференцируем по времени уравнение (7.16):

где - единичные векторы в направлении звезды в эпохи и . Тогда

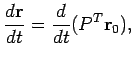
причем

где точкой обозначено дифференцирование по времени. Аналогично вычисляются другие производные. Так как

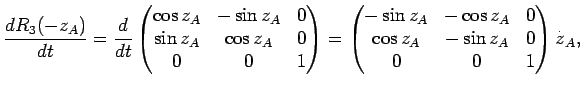
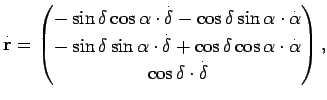
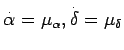то, очевидно, что прецессия влияет на скорость изменения экваториальных координат. С точностью до первого порядка . Это означает, что прецессия приводит к кажущемуся собственному движению звезд, которое может быть вычислено, если только матрица известна точно. Если углы вычисляются с ошибками, т.е. теория прецессии неточна, то эти ошибки приведут к ошибкам в собственных движениях звезд.

При наблюдениях внегалактических радиоисточников считается, что их собственные движения равны нулю. Следовательно, отличие от нуля правой части уравнения (7.21) означает неточность теории прецессии. Приравнять правую часть (7.21) нулю можно, изменив постоянные прецессии. На этом принципе основано уточнение этих постоянных из радиоинтерферометрических наблюдений.

С 1 января 2003 г. по решению Генеральной Ассамблеи МАС 2000 г. вводится новая теория прецессии-нутации взамен теории МАС1980. На основе анализа 20-летнего ряда наблюдений на РСДБ были определены поправки к (к дуге эклиптики эпохи J2000.0 между средними экваторами эпох и J2000.0) и углу между эклиптикой эпохи J2000.0 и средним экватором эпохи (см. рис. 7.4). Обозначим эти поправки как и , соответственно. Согласно принятой МАС новой теории эти поправки равны (по "Соглашениям" МСВЗ 2003 г.):

Заметим здесь, что точность определения и сильно завышена. На основе сравнения нескольких теорий прецессии-нутации можно сделать вывод, что ошибки и составляют 3-4 мс дуги.

Найдем изменение прецессионных величин . Пусть , . Тогда

. С точностью до первого порядка имеем:

Значит поправки к прецессионным величинам равны:

---

<< 7.1. Причины прецессии и | Оглавление | 7.3. Математическое описание прецессии >>

Публикации с ключевыми словами: астрометрия - сферическая астрономия - системы координат - шкалы времени Публикации со словами: астрометрия - сферическая астрономия - системы координат - шкалы времени
См. также: 80 лет со дня рождения Альберта Петровича Гуляева Руководство по практической работе с каталогом Hipparcos К 70-летию Вилена Валентиновича Нестерова Полная версия "Сферической астрономии" В.Е.Жарова Обзор геостационарной орбиты на двойном астрографе УАФО Отдел пульсарной астрометрии ПРАО АКЦ ФИАН Прямое определение расстояния до центра Галактики Все публикации на ту же тему >>