Астронет > Физические вопросы теории звездной эволюции

по текстам по ключевым словам в глоссарии по сайтам перевод

<< 2. Релятивистский газ с ... | Оглавление | 4. Вещество при больших ... >>

3. Уравнение состояния при наличии ядерного равновесия и процессов слабого взаимодействия

Когда температура вещества достигает нескольких миллиардов кельвинов, характерные времена ядерных реакций $t_{n}$ становятся меньше всех макроскопических времен и устанавливается равновесие относительно ядерного состава. В условиях ядерного равновесия концентрации ядер находятся из соотношения между химическими потенциалами ядер $\mu _{A,Z}$ , нейтронов $\mu _{n}$ и протонов $\mu _{p}$ , аналогично условию химического равновесия

$\mu_{A,Z}=Z\mu_{\mathrm{n}}+(A-Z)\mu_{\mathrm{n}}.$

(3.1)

Для нерелятивистских и невырожденных ядер имеем [145]

$\mu_{A,Z}=-kT\ln\left[\left(\AZ{m}kT\over 2\pi\hbar^2\right)^{3/2} {\AZ{g}\over \AZ{n}}\right]\AZ{m}c^2.$

(3.2)

Равновесная концентрация ядер из (3.1), (3.2) имеет вид

$\eqalign{ \AZ{n}&=\left(\pih\over kT\right)^{{3\over 2}(A-1)} \left(\AZ{m}\over {m_{\mathrm{p}}}^Z {m_{\mathrm{n}}}^{A-Z}\right)^{3/2} {\AZ{g}\over {g_{\mathrm{p}}}^Z {g_{\mathrm{n}}}^{A-Z}} \cr \noalign{\medskip} &\qquad\times\exp\left\{{[Zm_{\mathrm{p}}+(A-Z)m_{\mathrm{n}}-\AZ m]c^2\over kT}\right\} {n_{\mathrm{p}}}^Z {n_{\mathrm{n}}}^{A-Z}. \cr }$

(3.3)

В предэкспоненте достаточно положить $m_{n}=m_{p}=m_{u}$ , $m_{A,Z}=Am_{u}$ , а числитель в экспоненте есть энергия связи ядра $B_{A,Z}$ . Учтя также $g_{p}=g_{n}=2$ , получим

$\AZ n=\left(\pih\over m_{\mathrm{p}} kT\right)^{{3\over 2}(A-1)} {A^{3/2}\over 2^A}\AZ g e^{{\AZ B\over kT}} {n_{\mathrm{p}}}^Z {n_{\mathrm{n}}}^{A-Z}.$

В табл. 5 приведены спины $I$ , энергии связи $B$ наиболее устойчивых ядер, $g_{A,Z}=2I_{A,Z}+1$ . Благодаря экспоненциально быстрой зависимости скорости ядерных реакций от температуры (см. гл. 4), переход от застывшего ядерного состава к ядерному равновесию занимает узкую зону температур, где характерные времена ядерных реакций сравнимы с макроскопическими (тепловым или гидродинамическим) и где необходимо рассмотрение кинетики ядерных реакций. При данной температуре $T$ и плотности

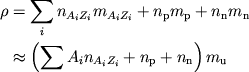$\eqalign{ \rho&=\sum_i n_{A_i Z_i}m_{A_i Z_i}+n_{\mathrm{p}} m_{\mathrm{p}}+n_{\mathrm{n}} m_{\mathrm{n}} \cr &\approx \left(\sum A_i n_{A_i Z_i}+n_{\mathrm{p}}+n_{\mathrm{n}}\right)m_{\mathrm{u}} \cr }$

(3.4)

для нахождения ядерного состава необходимо знать связь между концентрациями $n_{n}$ и $n_{p}$ .

Таблица 5. Энергии связи и спины ядер стабильных изотопов наиболее обильных элементов [135, 180]

Атомный номер	Элемент (изотоп)	Энергия связи $E_{b}$ , кэВ	Спин ядра I
1	$^{1}H$ , $^{2}H$	0.2225	1/2, 1
2	$^{3}He$ , $^{4}He$	7718, 28297	1/2, 0
6	$^{12}C$ , $^{13}C$	92165, 97112	0, 1/2
7	$^{14}N$ , $^{15}N$	104663, 115496	1, 1/2
8	$^{16}O$ , $^{17}O$ , $^{18}O$	127624, 131766, 139813	0, 5/2, 0
10	$^{20}Ne$ , $^{21}Ne$ , $^{22}Ne$	160651, 167412, 177778	0, 3/2, 0
11	$^{23}Na$	186570	3/2
12	$^{24}Mg$ , $^{25}Mg$ , $^{26}Mg$	198262, 205594, 216688	0, 5/2, 0
13	$^{27}Al$	224959	5/2
14	$^{28}Si$ , $^{29}Si$ , $^{30}Si$	236544, 245018, 255627	0, 1/2, 0
15	$^{31}P$	262925	1/2
16	$^{32}S$ , $^{33}S$ , $^{34}S$	271789, 280432, 291847	0, 3/2, 0
17	$^{35}Cl$ , $^{37}Cl$	298220, 317112	3/2, 3/2
18	$^{36}Ar$ , $^{38}Ar$ , $^{40}Ar$	306727, 327354, 343822	0, 0, 0
20	$^{40}Ca$ , $^{42}Ca$ , $^{43}Ca$	342063, 361900, 369832	0, 0, 7/2
	$^{44}Ca$ , $^{46}Ca$ , $^{48}Ca$	380969, 398787, 416014	0, 0, 0
24	$^{50}Cr$ , $^{52}Cr$ , $^{53}Cr$ , $^{54}Cr$	435061, 456364, 464304, 474024	0, 0, 3/2, 0
25	$^{55}Mn$	482091	5/2
26	$^{54}Fe$ , $^{56}Fe$ , $^{57}Fe$ , $^{58}Fe$	471779, 492280, 499926, 509969	0, 0, 1/2, 0
28	$^{58}Ni$ , $^{60}Ni$ , $^{61}Ni$	506484, 526871, 534691	0, 0, 3/2
	$^{62}Ni$ , $^{64}Ni$	545288, 561788	0, 0
$B_{A,Z}=\left( Zm_{p}+\left( A-Z\right) m_{n}-m_{A,Z}\right) c^{2}$
$m_{n}=m_{p}+m_{e}+782.5$ кэВ

Взаимопревращения протонов и нейтронов, как свободных, так и связанных в ядрах, происходят в реакциях слабого взаимодействия (см. гл. 5). Характерное время слабых процессов $t_{\beta }$ при высокой температуре значительно больше ядерного $t_{n}$ и может быть порядка микроскопического, гидродинамического или теплового. Нейтрино, возникающие при слабых взаимодействиях, свободно улетают из звезд. В этих условиях термодинамическое равновесие относительно реакций слабого взаимодействия отсутствует. Исключение составляют горячие нейтронные звезды, которые непрозначны для нейтрино с энергией $E_{\nu _{e}}\geq 1\mbox{~МэВ}$ . Термодинамические функции равновесного нейтринного газа $\nu _{e}$ , $\widetilde{\nu _{e}}$ -газа с $kT\gg m_{\mu _{e}}c^{2}$ ⁵ аналогичны электронным (2.56), где $\beta =\mu _{\nu _{e}}/kT$ , а величины $E_{\nu _{e}\widetilde{\nu _{e}}}$ , $P_{\nu _{e}\widetilde{\nu _{e}}}$ , $S_{\nu _{e}\widetilde{\nu _{e}}}$ в два раза меньше, чем $E_{e\pm }$ , $P_{e\pm }$ и $S_{e\pm }$ за счет статистического веса. В левой части первого соотношения (2.56), служащего для нахождения $\mu _{\nu _{e}}$ , $\rho /\mu _{Z}m_{u}$ вместо $\rho /\mu _{Z}m_{u}$ должна стоять величина, связанная с концентрацией лептонного заряда $Q_{\nu _{e}}:2\left( Q_{\nu _{e}}-n_{e-}+n_{e+}\right) =2\left( n_{\nu _{e}}-n_{\widetilde{\nu _{e}}}\right)$ . После таких замен все формулы п.д 2 применимы для равновесного нейтринного газа, а связь между $n_{p}$ и $n_{n}$ определяется соотношениями между химическими потенциалами

$\mu_{\mathrm{n}}=\mu_{\mathrm{p}}+\mute+\mu_{\nuet},\quad \mu_{\nuet}=-\mu_{\nue}.$

(3.5)

Второе соотношение (3.5) следует из равновесия реакции $\nu _{e}+\widetilde{\nu _{e}}\rightarrow e^{+}+e^{-}$ и условия (2.11). Равновесие других типов нейтрино $\nu _{\mu }$ и $\nu _{\tau }$ описывается аналогично $\nu _{e}$ , хотя оно вряд ли достижимо даже в горячих нейтронных звездах из-за большой массы их лептонов.

В условиях свободного улета нейтрино строгое нахождение связи $n_{p}$ и $n_{n}$ состоит в решении уравнений кинетики бета-процессов

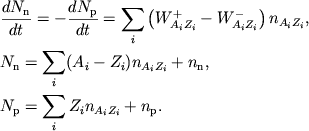$\eqalign{ &{dN_{\mathrm{n}}\over dt}=-{dN_{\mathrm{p}}\over dt} =\sum_i\left(W_{A_iZ_i}^+ -W_{A_iZ_i}^-\right)n_{A_iZ_i}, \cr &N_{\mathrm{n}}=\sum_i(A_i-Z_i)n_{A_i Z_i}+n_{\mathrm{n}}, \cr &N_{\mathrm{p}}=\sum_i Z_i n_{A_i Z_i}+n_{\mathrm{p}}. \cr }$

(3.6)

при известном начальном соотношении между $N_{n}$ и $N_{p}$ . В работе [328] параметр $N_{n}/N_{p}$ считался независимым при расчетах ядерного равновесия элементов группы железа. В первом соотношении (3.6) при суммировании нужно учитывать свободные нейтроны и протоны. Скорости бета-реакций ( $c^{-1}$ ) $W^{+}_{A,Z}=W_{A,Z}(e^{+}-\mbox{распад})+W_{A,Z}(e^{-}-\mbox{захват})$ и $W^{-}_{A,Z}=W_{A,Z}(e^{-}-\mbox{распад})+W_{A,Z}(e^{+}-\mbox{захват})$ рассмотрены в параграфе 19.

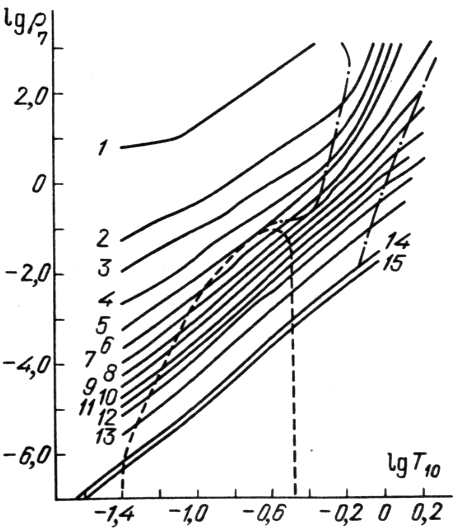Рис. 6. Изэнтропы вещества на плоскости $T$ , $\rho$ . Для 10⁹ < Т < 2^.10¹⁰К, 10⁵ < $\rho$ < 10¹⁰ г/см³ изэнтропы построены для равновесного химического состава по данным работы [114]. Штриховая линия разделяет области $\gamma_1$ > 4/3 и $\gamma_1$ < 4/3 и построена по данным расчетов [46]. Штрихпунктирные линии разделяют области $\gamma_1$ > 4/3 и $\gamma_1$ < 4/3 и построены по данным работы [114] с учетом распада железа. Цифры на рисунке соответствуют следующим иээнтропам: 1 - $S_{10}$ = 0,003981, 2 - $S_{10}$ = 0,01, 3 - $S_{10}$ = 0,01585, 4 - $S_{10}$ = 0,02512, 5 - $S_{10}$ = 0,03981, 6 - $S_{10}$ = 0,0631, 7 - $S_{10}$ = 0,1, 8 - $S_{10}$ = 0,1585, 9 - $S_{10}$ = 0,2512, 10 - $S_{10}$ = 0,3981, 11 - $S_{10}$ = 0,631, 12 - $S_{10}$ = 1,0, 13 - $S_{10}$ = 2,512, 14 - $S_{10}$ = 10, 15 - $S_{10}$ = 15,85, $S_{10} = S/10$ эрг г^-1 К^-1

Если в течение времени $t\gg t_{\beta }$ величины $T$ и $\rho$ в звезде меняются слабо, то достигается кинетическое равновесие по бета-процессам с $dN_{n}/dt=0$ в (3.6). В этом случае соотношения (3.6) однозначно определяют состав вещества [117-119, 224]. Для приближенного определения состава в условиях свободного улета нейтрино иногда используется соотношение (3.5) с $\mu _{\nu _{e}}=0$ . Расчеты в этом приближении сделаны в [114]. В ядерном равновесии учитывались ядра железа $^{56}Fe$ , включая семь первых возбужденных уровней, $^{4}He$ , $n$ и $p$ . Рост температуры ведет сначала к расщеплению ядер железа на $^{4}He$ и нуклоны, а затем к чисто нуклонному составу. При большой плотности основную часть свободных нуклонов составляют нейтроны. На рис. 6 из [46] приведены изэнтропы вещества на плоскости $\rho$ , $T$ и указаны области с $\gamma _{1}\lt 4/3$ , необходимые для анализа устойчивости (см. гл.12). В области ядерного равновесия использовались результаты [114].

<< 2. Релятивистский газ с ... | Оглавление | 4. Вещество при больших ... >>

Публикации с ключевыми словами: Эволюция звезд - физические процессы
Публикации со словами: Эволюция звезд - физические процессы

См. также:

Кошачий глаз в ширину и глубину

Двойная звезда φ Персея

Эта Киля в рентгеновских лучах

Туманность Кошачий глаз

Планетарная туманность Стухшее Яйцо

Туманность Эскимос в обновленный телескоп Хаббла

M27 - это не комета

Все публикации на ту же тему >>

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце