<< Фракталы в математике и Формирование структур >>
Методы обнаружения фрактальных структур
в астрофизических объектах
Для исследования свойств фрактальной структуры какого-либо физического фрактала необходимо иметь какой-либо алгоритм определения фрактальной размерности объекта по данным наблюдений. Существует весьма большое количество различных методов определения фрактальной размерности или заменяющих ее величин, однако все они базируются на классическом определении фрактальной размерности, данном Хаусдорфом. Некоторые из этих алгоритмов являются достаточно простыми и могут быть реализованы программно; некоторые представляют только математический интерес, поскольку являются неприводимыми и требуют бесконечного времени вычислений. Остановимся на некоторых методах, применение которых как к астрофизическим объектам представляется достаточно оправданным.
Одна из возможных характеристик фрактальной структуры - корреляционный
показатель. Пусть для ![]() точек
точек ![]() изучаемого множества
изучаемого множества ![]() в
пространстве
в
пространстве
![]() функция
функция
![]() - расстояние между
точками. Введем функцию
- расстояние между
точками. Введем функцию
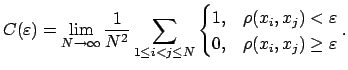 |
(4) |
Тогда корреляционным показателем
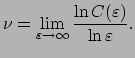 |
(5) |
Для самоподобной фрактальной структуры корреляционный показатель
Тем не менее в астрофизических приложениях чаще используются более простые методы, основанные на подсчетах количества элементов структуры, содержащихся в определенном объеме.
Пусть объект обладает самоподобной фрактальной структурой, состоит из
одинаковых элементов и в объемах, ограниченных концентрическими сферами
радиусов ![]() и
и ![]() , содержит соответственно
, содержит соответственно ![]() и
и ![]() элементов.
Полагаем, что
элементов.
Полагаем, что
| (6) |
а величина
где
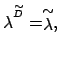 |
(8) |
определяющее величину
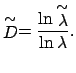 |
(9) |
Величина
![]() для самоподобных фракталов
совпадает с фрактальной размерностью
для самоподобных фракталов
совпадает с фрактальной размерностью ![]() . Коэффициент
. Коэффициент ![]() ,
называемый "префактором", равен
,
называемый "префактором", равен
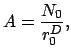 |
(10) |
где
Важное для астрофизических приложений соотношение следует из (7) для
систем, в которых все элементы имеют одну и ту же массу ![]() . Отношение
масс, содержащихся в соответствующих сферических объемах, записывается в
следующем виде:
. Отношение
масс, содержащихся в соответствующих сферических объемах, записывается в
следующем виде:
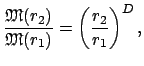 |
(11) |
откуда, следовательно,
Здесь ![]() означает расстояние от любой произвольно выбранной точки
структуры. При таком условии средняя плотность вещества в
произвольном сферическом объеме оказывается зависящей от размера
этого объема. Существенно, что это утверждение верно для всех
точек, входящих в структуру. Для реальных структур значения
означает расстояние от любой произвольно выбранной точки
структуры. При таком условии средняя плотность вещества в
произвольном сферическом объеме оказывается зависящей от размера
этого объема. Существенно, что это утверждение верно для всех
точек, входящих в структуру. Для реальных структур значения ![]() в
различных точках структуры могут получаться разными, что
обусловлено случайными отклонениями структуры от идеально
фрактальной, но если получаемые "локальные размерности" близки
друг к другу, то можно говорить о существовании фрактальной
структуры с размерностью, равной среднему значению локальных
размерностей для всех точек структуры.
в
различных точках структуры могут получаться разными, что
обусловлено случайными отклонениями структуры от идеально
фрактальной, но если получаемые "локальные размерности" близки
друг к другу, то можно говорить о существовании фрактальной
структуры с размерностью, равной среднему значению локальных
размерностей для всех точек структуры.
Более сложной является система, состоящая из объектов различной массы. Если структура системы фрактальна, то в этом случае множество, являющееся геометрическим "носителем" объектов, представляет собой мультифрактал.
В некоторых случаях (например, когда желательно исключить
возможные эффекты наблюдательной селекции) целесообразно
рассматривать не сферические объемы, а тела одинаковой, но
произвольной формы, отличающиеся размером. В таком случае
выражение (12) также остается истинным, однако ![]() приобретает смысл характерного размера, являющегося параметром
используемых объемов.
приобретает смысл характерного размера, являющегося параметром
используемых объемов.
К сожалению, в астрофизике часто отсутствует полная информация о
пространственной структуре наблюдаемого объекта. В таком случае
фрактальную размерность приходится определять по проекции объекта
на небесную сферу. Для многоугольников, кругов и других областей,
ограниченных обычными кривыми, отношение длины периметра ![]() к
величине
к
величине ![]() , где
, где ![]() - площадь области, является
величиной, не зависящей от размера области. Однако когда область
фрактальна, то фрактален и ее периметр. Результат измерения
величины
- площадь области, является
величиной, не зависящей от размера области. Однако когда область
фрактальна, то фрактален и ее периметр. Результат измерения
величины ![]() в этом случае зависит от используемого эталона длины.
Для фрактального периметра
в этом случае зависит от используемого эталона длины.
Для фрактального периметра ![]() , зависящего от величины
эталона
, зависящего от величины
эталона ![]() ,
,
| (13) |
Площадь же области, определяемая путем наложения на нее квадратов со стороной
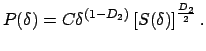 |
(14) |
Величина
Полученная величина ![]() относится к периметру проекции объекта.
Однако поскольку граница объекта является линией пересечения
поверхности пространственной структуры с плоскостью, то значение
относится к периметру проекции объекта.
Однако поскольку граница объекта является линией пересечения
поверхности пространственной структуры с плоскостью, то значение
![]() для пространственной структуры может быть получено на
основании так называемой "теоремы о сложении". Согласно этой
теореме при пересечении самоподобной фрактальной структуры
размерности
для пространственной структуры может быть получено на
основании так называемой "теоремы о сложении". Согласно этой
теореме при пересечении самоподобной фрактальной структуры
размерности ![]() со структурой размерности
со структурой размерности ![]() в пространстве
топологической размерности
в пространстве
топологической размерности ![]() получается структура, обладающая
размерностью
получается структура, обладающая
размерностью ![]() , равной
, равной
| (15) |
отсюда, в частности, следует, что фрактальная размерность пространственной структуры
<< Фракталы в математике и Формирование структур >>