Астронет > Колебания и волны

по текстам по ключевым словам в глоссарии по сайтам перевод

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

Вынужденные колебания под действием гармонической силы. Режимы медленных, быстрых и резонансных колебаний. Амплитудно-частотные и фазо-частотные характеристики. Баллистический режим колебаний. Установление колебаний. Характеристики различных колебательных систем. Параметрические колебания. Автоколебания.

В предыдущей лекции мы рассмотрели свободные затухающие колебания, возникающие при начальном кратковременном воздействии внешних сил на колебательную систему. Между тем, в повседневной практике мы сталкиваемся с незатухающими колебаниями, для поддержания которых необходимо подводить энергию к колебательной системе, чтобы компенсировать ее энергетические потери.

Одним из распространенных способов поддержания незатухающих колебаний является непрерывное воздействие на колеблющуюся массу периодической силы (вынуждающей силы)

$F(t) = F(t + T),$

(2.1)

меняющейся во времени $t$ , вообще говоря, произвольно в пределах периода длительностью $T$ . Если, например, такую силу приложить к колеблющейся массе описанного выше пружинного маятника (рис. 2.1), то уравнение ее движения примет вид:

$m\ddot {\displaystyle s} = - \Gamma \dot {\displaystyle s} - ks + F(t).$

(2.2)

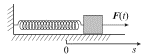Рис. 2.1.

Опыт показывает, что если сила внезапно начинает действовать (например, в момент времени $t = 0$ ), то маятник начнет постепенно раскачиваться, и спустя какое-то время его колебания установятся. По порядку величины время установления таких вынужденных колебаний будет совпадать с временем затухания $\tau = \delta ^{ - 1} = 2m / \Gamma .$ Далее мы сконцентрируем внимание именно на установившихся колебаниях. Естественно, что параметры таких колебаний будут зависеть от конкретного вида силы $F(t).$ Из математики хорошо известно, что любую периодическую функцию можно представить в виде ряда Фурье:

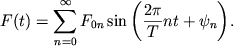$F(t) = {\displaystyle \sum\limits_{n = 0}^{\infty } {\displaystyle F_{0n} \sin \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle 2\pi }}{\displaystyle {\displaystyle T}}}nt + \psi _{n} } \right)} }.$

(2.3)

Физический смысл этого представления состоит в том, что периодическое воздействие $F(t)$ эквивалентно одновременному воздействию постоянной силы $F_{00}$ и набора гармонических сил с соответствующими амплитудами $F_{0n},$ начальными фазами $\psi _{n}$ и частотами $\omega _{n} = {\displaystyle \frac{\displaystyle {\displaystyle 2\pi }}{\displaystyle {\displaystyle T}}}n = \omega n,$ кратными низшей (основной) частоте $\omega = {\displaystyle \frac{\displaystyle {\displaystyle 2\pi }}{\displaystyle {\displaystyle T}}}.$

Чтобы получить полную картину вынужденных колебаний под действием силы (2.3), необходимо принять во внимание линейность уравнения (2.2). Это позволяет представить его решение $s(t)$ как сумму гармонических колебаний:

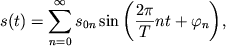$s(t) = {\displaystyle \sum\limits_{n = 0}^{\infty } {\displaystyle s_{0n} \sin \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle 2\pi }}{\displaystyle {\displaystyle T}}}nt + \varphi _{n} } \right)} },$

(2.4)

происходящих с установившимися амплитудами $s_{0n}$ и фазами $\varphi _{n}$ на частотах $\omega _{n}$ соответствующих гармоник вынуждающей силы (2.3). Каждое слагаемое в (2.4) может рассматриваться как вынужденное гармоническое колебание, происходящее под действием внешней гармонической силы с амплитудой $F_{0n}$ и частотой $\omega _{n} = {\displaystyle \frac{\displaystyle {\displaystyle 2\pi }}{\displaystyle {\displaystyle T}}}n.$

Амплитуды $s_{0n}$ и фазы $\varphi _{n}$ требуют определения, и мы перейдем сейчас к их нахождению.

Вынужденные колебания под действием гармонической силы.

Пусть внешняя сила меняется по гармоническому закону

$F(t) = F_{0} \sin \omega t.$

(2.5)

Уравнение (2.2) в этом случае принимает вид:

$m\ddot {\displaystyle s} = - \Gamma \dot {\displaystyle s} - ks + F_{0} \sin \omega t.$

(2.6)

Под действием этой силы маятник в установившемся режиме будет совершать гармонические колебания

$s(t) = s_{0} \sin (\omega t + \varphi _{0} ).$

(2.7)

Как показывает опыт, амплитуда $s_{0}$ и начальная фаза $\varphi _{0}$ (т.е. сдвиг фазы между смещением $s$ и силой $F$ ) установившихся колебаний зависят не только от амплитуды силы $F_{0}$ (что очевидно из уравнения (2.6)), но и от того, насколько частота вынуждающей силы $\omega$ отличается от собственной частоты колебаний маятника $\omega _{0} = \sqrt {\displaystyle k / m.}$ Наиболее сильно маятник будет раскачиваться, когда эти частоты практически совпадают: $\omega \approx \omega _{0} .$

Прежде чем приступить к нахождению $s_{0}$ и $\varphi _{0} ,$ заметим, что для механических колебательных систем не так просто с технической точки зрения осуществить воздействие гармонической силы непосредственно на движущуюся массу. Гораздо проще это сделать для электрических и оптических колебательных систем, например, для колебательного контура, подключенного к внешнему источнику переменного напряжения. Легко, однако, видеть, что можно поддерживать вынужденные колебания маятника, изображенного на рис. 2.1, иным способом, не прикладывая непосредственно внешнюю силу $F(t)$ к массе $m.$ Достаточно лишь эту силу приложить к левому концу свободной пружины так, чтобы этот конец двигался по гармоническому закону $\xi (t) = \xi _{0} \sin \omega t$ (рис. 2.2). Тогда удлинение пружины составит величину $s - \xi ,$ а сила упругости, приложенная к массе $m$ , будет равна $- k(s - \xi ).$ Поэтому уравнение движения массы $m$ запишется в виде:

$m\ddot {\displaystyle s} = - \Gamma \dot {\displaystyle s} - k(s - \xi ).$

(2.8)

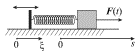Рис. 2.2.

Если принять во внимание, что сила упругости пружины в отсутствие смещения груза (s = 0) равна

$F(t) = k\xi (t) = k\xi _{0} \sin \omega t,$

(2.9)

то уравнение (2.8) полностью эквивалентно уравнению (2.6). Сила (2.9) выполняет роль внешней гармонической силы в классической схеме, изображенной на рис. 2.1. Эта сила легко может быть визуализирована, поскольку ее величина и направление однозначно определяется смещением подвижного левого конца пружины. Это, в свою очередь, дает возможность наглядно продемонстрировать фазовые соотношения между силой $F(t)$ (или смещением $\xi (t)$ ) и смещением $s(t)$ колеблющейся массы.

Перепишем уравнение (2.8) следующим образом:

$\ddot {\displaystyle s} + 2\delta \dot {\displaystyle s} + \omega _{0}^{2} s = {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle m}}}\sin \omega t,$

(2.10)

где $F_{0} = k\xi _{0} .$

Решение этого уравнения будем искать в виде гармонического колебания (2.7), где амплитуда $s_{0}$ и фаза $\varphi _{0}$ могут быть определены, если подставить (2.7) в (2.10). Мы сделаем это несколько позднее, а пока рассмотрим три важных режима вынужденных колебаний.

Медленные колебания.

Если частота вынуждающей силы $\omega$ значительно меньше $\omega _{0} ,$ то скорость $\dot {\displaystyle s}$ и ускорение $\ddot {\displaystyle s}$ колеблющейся массы будут очень малыми. Поэтому можно пренебречь первыми двумя членами в левой части уравнения (2.10) и записать его в приближенном виде:

$\omega _{0}^{2} s = {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle m}}}\sin \omega t.$

(2.11)

Его решение очевидно:

$s(t) = {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle m\omega _{0}^{2} }}}\sin \omega t = {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle k}}}\sin \omega t.$

(2.12)

В этом режиме смещение груза пропорционально внешней силе и не зависит от величины его массы $m$ . Решение (2.12) является, по существу, математическим выражением закона Гука для статической деформации пружины. Поэтому этот режим можно назвать квазистатическим (почти статическим). Амплитуда колебаний в соответствии с этим законом равна $s_{0} = F_{0} / k,$ а смещение $s(t)$ изменяется в фазе с внешней силой.

В схеме, изображенной на рис. 2.2, это эквивалентно тому, что смещение массы $m$ практически повторяет смещение левого конца пружины:

$s(t) = {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle k}}}\sin \omega t = {\displaystyle \frac{\displaystyle {\displaystyle k\xi _{0} }}{\displaystyle {\displaystyle k}}}\sin \omega t = \xi (t),$

(2.13)

поскольку $F_{0} = k\xi _{0} .$ Это и не удивительно, т.к. для движения массы $m$ с пренебрежимо малым ускорением $\ddot {\displaystyle s}$ не требуется больших деформаций пружины: $s(t) - \xi (t) \approx 0.$

Назад| Вперед

Публикации с ключевыми словами: колебания - волны Публикации со словами: колебания - волны
См. также: Колебания и волны

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

Колебания и волны. Лекции.

Лекция 2

Вынужденные колебания под действием гармонической силы.

Медленные колебания.