Астронет > Колебания и волны

по текстам по ключевым словам в глоссарии по сайтам перевод

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

Распространение возмущений в системе с большим числом степеней свободы. Скорость распространения. Возбуждение волн. Группа волн и ее скорость. Волновое уравнение. Волны в сплошном шнуре. Отражение волн. Возбуждение стоячих волн в шнуре. Моды колебаний. Волны в упругих телах. Поперечные волны. Энергия, переносимая волной. Вектор Умова. Продольные волны. Скорость волн в тонком и толстом стержнях. Отражение и прохождение волн на границах двух сред. Удельное волновое сопротивление.

Распространение возмущений в системе с большим числом степеней свободы.

Рассмотрим колебания $N \gg 1$ масс на резиновом шнуре (рис. 4.1а). Отклоним несколько масс в середине шнура от положения равновесия (рис 4.1б), и затем отпустим их в момент времени $t = 0.$ Как показывает опыт, эта начальная конфигурация, представляющая собой по форме импульс, с течением времени трансформируется в два одинаковых импульса, которые побегут в разные стороны с некоторой конечной скоростью c (рис. 4.1в). Эти импульсы добегут до концов шнура, изменят свою полярность при отражении и побегут в обратном направлении (рис. 4.1г). После встречи в середине шнура они отразятся еще раз, восстановят исходную полярность и спустя время $\Delta t = 2\ell / c$ вновь встретятся в середине, сформировав исходный импульс. Затем этот процесс с периодом $\Delta t$ будет повторяться до тех пор, пока импульсы не затухнут из-за диссипации энергии.

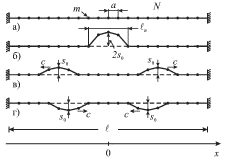Рис. 4.1.

С точки зрения повседневного опыта в этом нет ничего удивительного, поскольку смещения группы масс ведут к возникновению упругих сил, стремящихся вернуть эту группу в положение равновесия и одновременно вывести соседние частицы из положения равновесия.

С точки зрения описания колебаний "на языке мод" также понятно, что отклонив, а затем отпустив группу частиц, мы возбуждаем много мод. Колебания всех $N$ частиц происходят одновременно на нескольких нормальных частотах $\omega _{p}.$ Все эти частоты различны, и сумма нормальных колебаний представляет собой биения. Поскольку через время, равное периоду биений, колебания группы частиц в центре шнура восстановятся, то очевидно, что период биений равен упоминавшемуся несколько ранее времени $\Delta t = 2\ell / c.$

Определим скорость с, исходя из представления о биениях, как суперпозиции нормальных колебаний. Для этого вначале перепишем дисперсионное соотношение (3.55) в виде

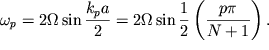$\omega _{p} = 2\Omega \sin {\displaystyle \frac{\displaystyle {\displaystyle k_{p} a}}{\displaystyle {\displaystyle 2}}} = 2\Omega \sin {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle p\pi }}{\displaystyle {\displaystyle N + 1}}}} \right).$

(4.1)

Строго говоря, при наличии многих частот в спектре колебаний, даваемых формулой (4.1), биения не будут периодическими - начальная конфигурация не повторяется. Визуально это будет проявляться в искажении формы бегущих импульсов, если длина импульса $\ell _{и} \geq a$ (импульс "накрывает" мало частиц), а шнур достаточно длинный. Говорят, что искажение импульса связано с дисперсией "среды" (шнура с массами), по которой импульс распространяется.

Это искажение будет ничтожным, если $\ell _{и} \gg a$ (группа состоит из большого числа колеблющихся масс). Так обычно и происходит при распространении возмущений в твердом теле, где $a\sim 10^{ - 10} м$ (расстояние между узлами кристаллической решетки, около которых колеблются атомы).

Если $\ell _{и} \gg a,$ то в спектре колебаний доминируют низшие моды, которые характеризуются волновыми числами $k_{p},$ где $p = I, II, III, \ldots \ll N.$ Частоты этих мод получаются из формулы (4.1):

$\omega _{p} = \Omega ak_{p} = {\displaystyle \frac{\displaystyle {\displaystyle \Omega \pi }}{\displaystyle {\displaystyle N + 1}}} \cdot p; p = I, II, III, \ldots$

(4.2)

Здесь использовано приближение $\sin x \approx x$ при $x \ll 1.$ Эта зависимость $\omega _{p} (k_{p} )$ изображена на рис. 4.2.

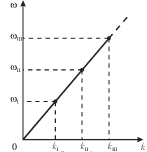Рис. 4.2.

Обратим внимание, что низшие частоты располагаются эквидистантно: $\Delta \omega = \omega _{II} - \omega _{I} = \omega _{III} - \omega _{II} = \ldots$ Поэтому период биений (см. также формулу (3.14)) получается равным:

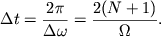$\Delta t = {\displaystyle \frac{\displaystyle {\displaystyle 2\pi }}{\displaystyle {\displaystyle \Delta \omega }}} = {\displaystyle \frac{\displaystyle {\displaystyle 2(N + 1)}}{\displaystyle {\displaystyle \Omega }}}.$

(4.3)

Если учесть, что длина шнура $\ell = a\left( {\displaystyle N + 1} \right),$ то скорость движения импульса в среде без дисперсии равна:

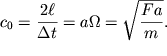$c_{0} = {\displaystyle \frac{\displaystyle {\displaystyle 2\ell }}{\displaystyle {\displaystyle \Delta t}}} = a\Omega = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle Fa}}{\displaystyle {\displaystyle m}}}}.$

(4.4)

Если мы будем увеличивать число масс $N$ на шнуре фиксированной длины, тем самым уменьшая расстояние $а,$ то мы сделаем предельный переход к непрерывному распределению масс - т.е. к однородному весомому шнуру, при этом

$\rho _{1} = m / a$

(4.5)

является массой единицы длины однородного шнура (иногда употребляют термин "плотность единицы длины"). Поэтому окончательно для скорости распространения импульса произвольной формы по шнуру имеем

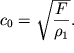$c_{0} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle F}}{\displaystyle {\displaystyle \rho _{1} }}}}.$

(4.6)

Например, в случае тонкого резинового шланга с линейной плотностью $\rho _{1} \sim 0,1 кг/м,$ натянутого с силой $F\sim 10^{2} Н,$ скорость движения импульса получается равной $c_{0} \sim 30 м/с.$ Такая сравнительно небольшая величина скорости позволяет легко наблюдать распространение и отражение импульса.

Итак, подведем некоторые итоги.

1. Если пренебречь периодической структурой среды, то скорость $c_{0}$ распространения импульса не зависит от его формы, а сам импульс при распространении не искажается (нет дисперсии).

2. Если ось x направить вдоль шнура и задать начальное возмущение (в момент $t = 0$ ) в виде $s(x),$ то с течением времени возмущение шнура будет иметь вид:

${\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}s(x - c_{0} t) + {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}s(x + c_{0} t).$

(4.7)

Первое слагаемое описывает возмущение, бегущее со скоростью $c_{0}$ в положительном направлении оси х, указанном на рис. 4.1, а второе соответствует импульсу, распространяющемуся в противоположном направлении.

3. У концов невесомого шнура с массами оба импульса отражаются. Отраженный импульс имеет противоположную полярность (направление смещения $s$ ) по сравнению с падающим.

Аналогичные граничные условия реализуются для сплошного массивного шнура с закрепленными концами (рис. 4.3).

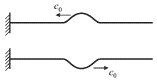Рис. 4.3.

4. В области перекрытия бегущих импульсов образуется колебание, называемое стоячей волной. Так мы приходим к понятиям бегущих и стоячих волн, при этом стоячая волна может рассматриваться как суперпозиция волн, бегущих в противоположных направлениях.

Возбуждение волн.

Рассмотрим колебания невесомого шнура с грузами, правый конец которого закреплен, а левый под действием внешней силы в момент времени $t = 0$ начинает смещаться по гармоническому закону:

$s(t) = s_{0} \sin \omega t.$

(4.8)

Под действием этой силы грузы, связанные друг с другом отрезками натянутого шнура, рано или поздно начнут совершать вынужденные гармонические колебания с частотой $\omega.$ Естественно, что систему грузов (по аналогии с системой с двумя грузами) можно заметно раскачать лишь в случае резонанса, когда частота $\omega$ совпадает с одной из нормальных частот $\omega _{p}.$

Вначале придут в движение грузы вблизи левого подвижного конца шнура, а с течением времени в колебания будут вовлекаться все новые грузы.

Такие колебания представляют собой волновой процесс (волну), распространяющийся "слева - направо" с некоторой скоростью $c_{p}.$ На рис. 4.4 изображены положения колеблющихся масс в некоторый момент времени $t_{0}.$ Поскольку грузы колеблются "поперек" направления распространения (оси Oх), то волна называется поперечной. Эта волна добежит до правого закрепленного конца шнура и отразится. После этого будут существовать две волны: исходная бегущая (иногда ее называют падающей волной) и отраженная волна, которая бежит навстречу падающей. Спустя время $\Delta t = 2\ell / c_{p}$ отраженная волна достигнет левого конца, снова отразится, и "сформируется" мода колебаний. Конфигурация этой моды задается волновым числом $k_{p}$ (см. соотношение (4.1)).

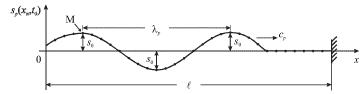Рис. 4.4.

Рассмотрим подробнее падающую волну с этим $k_{p}.$ Пространственный период $\lambda _{p},$ изображенный на рис. 4.4 как минимальное расстояние между массами, колеблющимися в фазе, называется длиной волны. Длина волны связана с волновым числом $k_{p}$ соотношением:

$k_{p} = 2\pi / \lambda _{p}.$

(4.9)

Если силы вязкого трения, приложенные к каждому из грузов, малы, то амплитуды колебаний всех грузов будут одинаковы и равны $s_{0}.$ Теперь мы можем записать уравнение бегущей волны - уравнение, описывающее смещение любой из масс в произвольный момент времени. Для частоты $\omega _{p},$ волнового числа $k_{p}$ и амплитуды $s_{0}$ оно имеет вид:

$\begin{array}{l} s_{p} (x_{n},t) = s_{0} \sin (\omega _{p} t - k_{p} x_{n} ); \\ x_{n} = a; 2a; \ldots; na; \ldots; Na. \\ \end{array}$

(4.10)

Выражение $\varphi = \omega _{p} t - k_{p} x_{n}$ называется фазой волны. Уравнение (4.10) отражает тот факт, что все массы колеблются с одинаковой частотой $\omega _{p},$ имеют одинаковую амплитуду $s_{0},$ однако эти колебания различаются по фазе $\varphi.$

Назад| Вперед

Публикации с ключевыми словами: колебания - волны Публикации со словами: колебания - волны
См. также: Колебания и волны

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

Колебания и волны. Лекции.

Лекция 4

Распространение возмущений в системе с большим числом степеней свободы.

Возбуждение волн.