<< 2. Геометрия небесной сферы | Оглавление | 4. Суточное вращение >>
- 3.1. Горизонтальная система координат
- 3.2. Первая экваториальная система координат
- 3.3. Вторая экваториальная система координат
3. Системы небесных координат
Положение небесных светил на небесной сфере однозначно определяется двумя сферическими координатами. Сферические координаты точки представляют собой дуги больших кругов сферы, выраженные в градусной или часовой мере. Хорошо известным примером таких сферических координат являются координаты точки на поверхности Земли - широта и долгота. Существует несколько систем астрономических координат. Эти системы отличаются одна от другой выбором основной плоскости и началом отсчета.
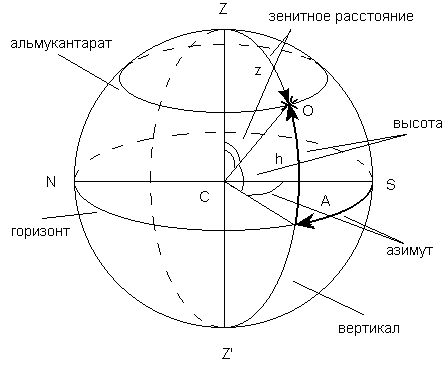
3.1. Горизонтальная система координат
Основной плоскостью является плоскость истинного горизонта, а началом отсчета - точка юга S. Координатами являются высота и азимут (рис. 5).
Высота светила над горизонтом, h, - это угловое расстояние от истинного горизонта, измеряемое по вертикалу светила (аналог широты). Высота светила может изменяться в пределах от -90o до 90o. Отрицательная высота означает, что светило находится под горизонтом. Пример: высота зенита равна 90o.
Вместо высоты светила в качестве первой горизонтальной координаты часто
употребляют зенитное расстояние z - угловое расстояние светила от
зенита, измеряемое по вертикалу светила. Существует простая связь между
зенитным расстоянием и высотой светила
| z+h = 90o. | (1) |
Зенитное расстояние может изменяться в пределах от 0o до 180o, причем светила с зенитным расстоянием больше 90o лежат ниже горизонта и являются ненаблюдаемыми.
Второй горизонтальной координатой является азимут А - это угловое расстояние от точки юга S до пересечения вертикала светила с горизонтом, отсчитываемое вдоль горизонта по часовой стрелке. Азимут может принимать значения от 0o до 360o и носит еще название астрономического азимута, в отличие от геодезического азимута, отсчитываемого от точки севера N по часовой стрелке.
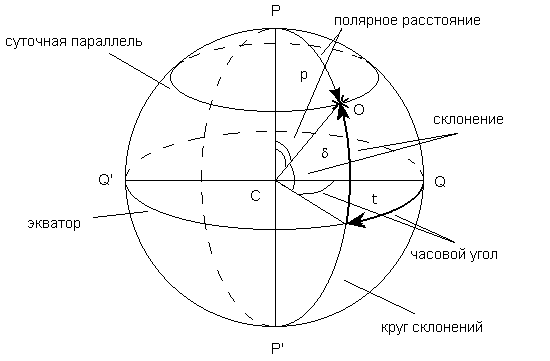
3.2. Первая экваториальная система координат
Основной плоскостью является плоскость небесного экватора, началом отсчета - точка Q. Координатами являются склонение и часовой угол (рис. 6).
Склонение светила, ![]() - это угловое расстояние от небесного
экватора до светила, отсчитываемое по кругу склонения. Склонение изменяется
в пределах от -90o до 90o, причем светила с
- это угловое расстояние от небесного
экватора до светила, отсчитываемое по кругу склонения. Склонение изменяется
в пределах от -90o до 90o, причем светила с ![]() 0 находятся к
северу от экватора, а с
0 находятся к
северу от экватора, а с ![]() 0 - к югу от него. Реже вместо склонения
используется полярное расстояние, p, - это угловое расстояние от
светила до полюса.
0 - к югу от него. Реже вместо склонения
используется полярное расстояние, p, - это угловое расстояние от
светила до полюса.
Часовой угол, t, - это дуга небесного экватора между небесным меридианом и кругом склонения светила. Отсчитывается от точки Q по часовой стрелке. Изменяется в пределах от 0o до 360o в градусной мере или от 0h до 24h в часовой мере (360o соответствует 24h, 1h - 15o, 1m - 15', 1s - 15").
Координаты звезд в горизонтальной и первой экваториальной системах координат изменяются из-за суточного вращения Земли, так как в них начало отсчета привязано к вращающейся Земле (точка юга S и точка Q лежат на небесном меридиане). Значит, для того, чтобы координаты звезд не изменялись из-за суточного вращения, необходимо выбрать точку отсчета, неподвижную относительно звезд и участвующую в суточном вращении. В качестве такой точки отсчета была выбрана точка весеннего равноденствия, и система координат, в которой звезды не изменяют свои координаты из-за суточного вращения, называется второй экваториальной системой координат.
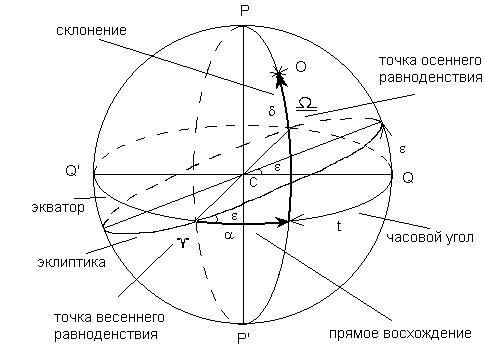
3.3. Вторая экваториальная система координат
Большой круг небесной сферы, по которому в течение года кажущимся образом
перемещается центр Солнца вследствие годичного обращения Земли вокруг
Солнца, называется эклиптикой. Эклиптика наклонена к экватору под
углом
![]() . Точки пересечения эклиптики с экватором
называются точками равноденствий. Та точка, в которой Солнце переходит из южной
части небесной сферы в северную, называется точкой весеннего равноденствия
. Точки пересечения эклиптики с экватором
называются точками равноденствий. Та точка, в которой Солнце переходит из южной
части небесной сферы в северную, называется точкой весеннего равноденствия
![]() , а противоположная - точкой осеннего равноденствия
, а противоположная - точкой осеннего равноденствия
![]() .
.
Во второй экваториальной системе координат основной плоскостью, как и в первой,
является плоскость небесного экватора, а началом отсчета - точка весеннего
равноденствия (рис. 7). Первой координатой также является склонение
![]() . Второй координатой, прямым восхождением
. Второй координатой, прямым восхождением ![]() , является
дуга небесного экватора от точки весеннего равноденствия до круга склонения
светила, отсчитываемая против часовой стрелки. Как и часовой угол, прямое
восхождение измеряется в часовой мере.
, является
дуга небесного экватора от точки весеннего равноденствия до круга склонения
светила, отсчитываемая против часовой стрелки. Как и часовой угол, прямое
восхождение измеряется в часовой мере.
Задачи
5. Найти в Атласе Цели Бечваржа (1962) звезды с координатами на эпоху 1950.0:
| 3h 22m | 8o51' | 7h 25m | 8o24' |
| 9h 43m | 24o00' | 18h 04m | 9o33' |
| 9h 28m | 63o17' | 14h 43m | 27o17' |
| 15h 14m | -9o12' | 6h 41m | 25o11' |
6. Найти по тому же атласу координаты на эпоху 1950.0 следующих звезд:
Вега (![]() ), Полярная (
), Полярная (![]() ), Гемма (
), Гемма (![]() ),
Бетельгейзе (
),
Бетельгейзе (![]() ), Сириус (
), Сириус (![]() ), Альтаир (
), Альтаир (![]() ),
Денеб (
),
Денеб (![]() ), Капелла (
), Капелла (![]() ), Арктур (
), Арктур (![]() ),
Спика (
),
Спика (![]() ).
).
<< 2. Геометрия небесной сферы | Оглавление | 4. Суточное вращение >>
|
Публикации с ключевыми словами:
задача - общая астрономия - Небесная сфера - системы координат - суточное вращение - рефракция - Сумерки - время - движение планет - расстояние - звезды - галактика
Публикации со словами: задача - общая астрономия - Небесная сфера - системы координат - суточное вращение - рефракция - Сумерки - время - движение планет - расстояние - звезды - галактика | |
См. также:
Все публикации на ту же тему >> | |