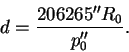<< 10. Движение планет | Оглавление | 12. Физические характеристики звезд >>
11. Определение расстояний до небесных тел. Параллакс.
Прямое определение расстояний до сравнительно близких небесных тел основано на явлении параллактического смещения. Суть его заключается в следующем. Близкий предмет при наблюдении его из разных точек проецируется на различные расположенные далеко предметы. Так, держа вертикально карандаш на фоне далекого многоквартирного дома, мы видим его левым и правым глазом на фоне разных окон. Для тел Солнечной системы такое смещение на фоне звезд заметно уже при наблюдении из точек, разнесенных на расстояние, сравнимое с радиусом Земли, а для близких звезд - при наблюдениях из точек, разнесенных на расстояние, сравнимое с радиусом орбиты Земли.
11.1. Горизонтальный экваториальный параллакс
Координаты небесных тел, определенные из разных точек земной поверхности,
вообще говоря различны, и называются топоцентрическими координатами.
Правда, это заметно лишь для тел Солнечной системы.
Для устранения этой неопределенности все координаты тел Солнечной системы
приводят к центру Земли и называют геоцентрическими.
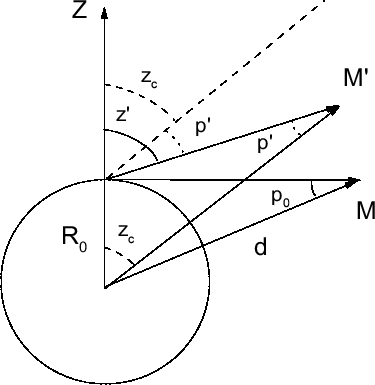
Угол между направлениями на какое-либо светило из
данной точки земной поверхности и из центра Земли называется суточным
параллаксом p' светила (рис. 22). Очевидно, что суточный параллакс равен
нулю для светила, находящегося в зените, и максимален для светила на горизонте.
Такой максимальный параллакс называется горизонтальным параллаксом
светила p. Горизонтальный параллакс связан с суточным простым соотношением:
По сути дела, p - это угол, под которым виден радиус Земли с данного светила. Однако Земля не является идеальным шаром и сплюснута к полюсам. Поэтому на каждой широте радиус Земли свой и горизонтальные параллаксы одного и того же светила разные. Для устранения этих различий принято вычислять горизонтальный параллакс для экваториального радиуса Земли (R0 = 6378 км) и называть его горизонтальным экваториальным параллаксом p0.
Суточный параллакс необходимо учитывать при измерении высот и зенитных
расстояний тел Солнечной системы и вносить поправку, приводя наблюдение к
центру Земли:
Измерив горизонтальный экваториальный параллакс светила p0, можно определить
расстояние d до него, т.к.
Заменив синус малого угла p0 значением самого угла, выраженным в радианах, и имея в виду, что 1 радиан равен 206265", получим искомую формулу:
Замена синуса угла самим углом допустима, так как наибольший из известных горизонтальный экваториальный параллакс Луны равен 57' (у Солнца p0=8".79).
В настоящее время расстояния до тел Солнечной системы с гораздо большей точностью измеряются методом радиолокации.
11.2. Годичный параллакс
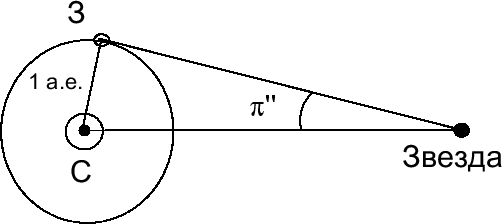
Угол, под которым с какой-либо звезды виден радиус земной орбиты a, при
условии, что он перпендикулярен направлению на нее, называется
годичным параллаксом ![]() звезды (рис. 23).
звезды (рис. 23).
По аналогии с горизонтальным экваториальным параллаксом, зная годичный
параллакс, можно определять расстояния до звезд:
В километрах расстояния до звезд измерять неудобно, поэтому обычно пользуются внесистемной единицей - парсеком пк, определяемой как расстояние, с которого параллакс равен 1". Само название составлено из первых слогов слов параллакс и секунда. Нетрудно убедиться, что 1 пк = 206 265 а.е. = 3.086
Расстояние до звезды в парсеках определяется через величину годичного
параллакса особенно просто
Задачи
60. (477) Параллакс Солнца p0=8".8, а видимый угловой радиус
Солнца
![]() . Во сколько раз радиус Солнца больше радиуса
Земли?
. Во сколько раз радиус Солнца больше радиуса
Земли?
Решение: Так как параллакс Солнца есть ни что иное, как угловой радиус
Земли, видимый с Солнца, следовательно, радиус Солнца во столько же раз больше
радиуса Земли, во сколько его угловой диаметр больше параллакса
![]() .
.
61. (482) В момент кульминации наблюденное зенитное расстояние центра Луны (p0=57') было 50o 00' 00". Исправить это наблюдение за влияние рефракции и параллакса.
Решение: За счет рефракции наблюденное топоцентрическое зенитное
расстояние меньше истинного топоцентрического, т.е.
![]() . Истинное топоцентрическое
зенитное расстояние больше геоцентрического на величину суточного параллакса
. Истинное топоцентрическое
зенитное расстояние больше геоцентрического на величину суточного параллакса
![]() .
.
62.(472) Чему равен горизонтальный параллакс Юпитера, когда он находится от Земли на расстоянии 6 а.е. Горизонтальный параллакс Солнца p0=8".8.
63. (474) Наименьшее расстояние Венеры от Земли равно 40 млн. км. В этот момент ее угловой диаметр равен 32".4. Определить линейный радиус этой планеты.
64. (475) Зная, что для Луны p0=57'02".7, а ее угловой радиус в это время rЛ=15'32".6, вычислить расстояние до Луны и ее линейный радиус, выраженные в радиусах Земли, а так же площадь поверхности и объем Луны по сравнению с таковыми для Земли.
65. (483) Наблюденное зенитное расстояние верхнего края Солнца
составляет 64o 55' 33", а его видимый радиус
![]() . Найти
геоцентрическое зенитное расстояние центра Солнца, учтя рефракцию и параллакс.
. Найти
геоцентрическое зенитное расстояние центра Солнца, учтя рефракцию и параллакс.
66. Из наблюдений известны годичные параллаксы ![]() звезд Вега
(
звезд Вега
(![]() )
)
![]() , Сириус
(
, Сириус
(![]() )
)
![]() , Денеб
(
, Денеб
(![]() )
)
![]() . Определить расстояние до этих звезд
в пк и в а.е.
. Определить расстояние до этих звезд
в пк и в а.е.
<< 10. Движение планет | Оглавление | 12. Физические характеристики звезд >>
|
Публикации с ключевыми словами:
задача - общая астрономия - Небесная сфера - системы координат - суточное вращение - рефракция - Сумерки - время - движение планет - расстояние - звезды - галактика
Публикации со словами: задача - общая астрономия - Небесная сфера - системы координат - суточное вращение - рефракция - Сумерки - время - движение планет - расстояние - звезды - галактика | |
См. также:
Все публикации на ту же тему >> | |