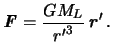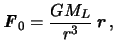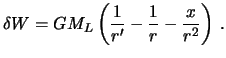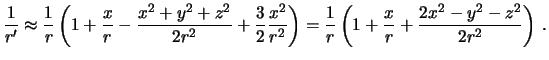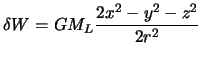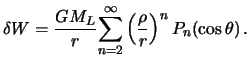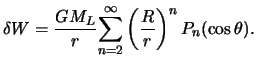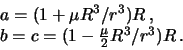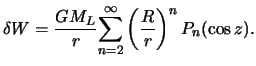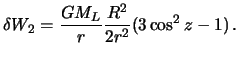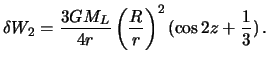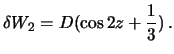<< 5.2 Температура в недрах | Оглавление | 6.2 Типы приливных волн >>
6. Приливы
Разделы
- 6.1 Приливообразующий потенциал
- 6.2 Типы приливных волн
- 6.3 Наблюдения приливных явлений на Земле
- 6.4 Космогоническое значение исследования приливов
6.1 Приливообразующий потенциал
Подразделы- 6.1.1 Приливная деформация уровенной поверхности планеты
- 6.1.2 Преобразование формулы для приливообразующего потенциала
Всем хорошо известен морской прилив, когда два раза в сутки вода поднимается у морских берегов, затем вновь откатывается от берега. Но прилив существует не только на море, но и на суше. Два раза в сутки поверхность земли, на которой выстроены все дома, улицы, дороги, поднимаются и опускаются. В Москве амплитуда этих колебаний составляет приблизительно 0,5 м. Но мы этого не замечаем. Отчего это происходит?
Как известно, результатом действия силы на тело является либо его ускорение, если оно свободно и не взаимодействует с другими телами, либо его деформация, если такое взаимодействие существует. Притяжения Луны и Солнца нашей планеты сообщают ей ускорение, которое она имеет, совершая движение по орбите. Однако не все части планеты испытывают одинаковое притяжение. В качестве притягивающего тела возьмем пока только Луну. Максимальное притяжение Луной испытывают те части Земли, для которых она находится строго в зените, а минимальное -- в надире. Центр масс Земли находится в промежуточном положении. Результирующая сила притяжения планеты приложена к центру масс. Она сообщает Земле поступательное ускорение. Для описания процессов в системе отсчета, связанной с Землей, то есть в неинерциальной системе координат, кроме упомянутых сил притяжения необходимо ввести силу инерции, равную массе какого-либо пробного тела умноженную на ускорение системы отсчета и направленную в сторону, противоположную ускорению системы отсчета.
Пренебрегая размером, строением и формой Луны, запишем удельную силу
притяжения пробного тела, находящегося на Земле. Пусть ![]() -- радиус-вектор, направленный от пробного тела в сторону Луны,
-- радиус-вектор, направленный от пробного тела в сторону Луны, ![]() -- длина
этого радиус-вектора, тогда сила притяжения этого тела Луной будет равна
-- длина
этого радиус-вектора, тогда сила притяжения этого тела Луной будет равна
Здесь ![]() -- селеноцентрическая гравитационная постоянная. Пробное тело
поместим в точку
-- селеноцентрическая гравитационная постоянная. Пробное тело
поместим в точку ![]() . Сила притяжения пробного тела помещенного в центр
масс Земли будет равна
. Сила притяжения пробного тела помещенного в центр
масс Земли будет равна
где
![]() и
и ![]() соответственно радиус-вектор, соединяющий центры масс
Земли и Луны, и его абсолютная величина. Тогда приливной силой называется разность этих
двух сил притяжения
соответственно радиус-вектор, соединяющий центры масс
Земли и Луны, и его абсолютная величина. Тогда приливной силой называется разность этих
двух сил притяжения
В формулах (6.1) и (6.2) притягивающее тело (Луна) рассматривается как материальная точка или шар со сферически симметричным распределением масс
Силовая функция притяжения пробного тела Луной ничем не отличается от
силовой функции притяжения шара (материальной точки), то есть она равна
![]() . Что касается второй силы, приложенной к центру масс и
являющейся силой инерции для всех материальных точек Земли, то она строго
постоянная. Для получения силовой функции для этой силы нам необходимо
ввести временную систему координат. Ось Ox проведем из центра Земли и направим
в сторону Луны. Направления двух других осей -- произвольные. Тогда силовая
функция для силы
. Что касается второй силы, приложенной к центру масс и
являющейся силой инерции для всех материальных точек Земли, то она строго
постоянная. Для получения силовой функции для этой силы нам необходимо
ввести временную систему координат. Ось Ox проведем из центра Земли и направим
в сторону Луны. Направления двух других осей -- произвольные. Тогда силовая
функция для силы
![]() , очевидно, равна
, очевидно, равна
![]() . Приливообразующий потенциал равен разности этих двух силовых функций. Обозначив его через
. Приливообразующий потенциал равен разности этих двух силовых функций. Обозначив его через
![]() , будем иметь
, будем иметь
Постоянную
![]() определим при условии, что приливообразующий потенциал в центра
Земли равен нулю. При этом
определим при условии, что приливообразующий потенциал в центра
Земли равен нулю. При этом ![]() ,
, ![]() .
Поэтому
.
Поэтому
![]() . Следовательно, для
приливообразующего потенциала можно записать
. Следовательно, для
приливообразующего потенциала можно записать
Поскольку
![]() , то
, то
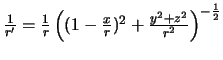 .
.
Полагая отношения
![]() малыми, последнее выражение можно представить следующим
образом
малыми, последнее выражение можно представить следующим
образом
Подставим полученное выражение в (6.4), получим
Выражение для приливообразующего потенциала можно уточнить, если в (6.4)
отношение ![]() заменить разложением в ряд по полиномам Лежандра, подобно тому,
как мы делали при выводе гравитационного потенциала планеты.
Пусть
заменить разложением в ряд по полиномам Лежандра, подобно тому,
как мы делали при выводе гравитационного потенциала планеты.
Пусть ![]() --
расстояние точки
--
расстояние точки ![]() от центра планеты ( от начала сферической системы
координат), а
от центра планеты ( от начала сферической системы
координат), а ![]() -- геоцентрическое зенитное расстояние притягивающего тела
(Луны), тогда
-- геоцентрическое зенитное расстояние притягивающего тела
(Луны), тогда
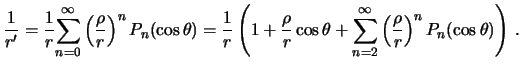
Поскольку
![]() , получим
, получим
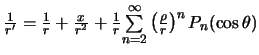 . Поставляя полученное выражение в формулу для приливообразующего
потенциала (6.4), окончательно получим
. Поставляя полученное выражение в формулу для приливообразующего
потенциала (6.4), окончательно получим
Остается определить приливообразующий потенциал на поверхности планеты.
Поскольку на поверхности сферической планеты ![]() , то
, то
6.1.1 Приливная деформация уровенной поверхности планеты
Приливное возмущение потенциала неизбежно деформирует уровенную поверхность
планеты. Выполним приближенную оценку этих искажений. Для простоты будем
считать, что Земля шар со сферически симметрично распределенной массой.
Тогда ее невозмущенный гравитационный потенциал на поверхности планеты имеет
простой вид ![]() . Для точки
. Для точки ![]() , находящейся на расстоянии
, находящейся на расстоянии ![]() от центра сферы
гравитационный потенциал Земли равен
от центра сферы
гравитационный потенциал Земли равен ![]() .
Добавляя сюда приливной потенциал,
получим возмущенную поверхность уровня
.
Добавляя сюда приливной потенциал,
получим возмущенную поверхность уровня
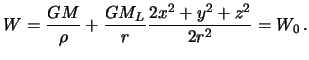
В качестве константы мы возьмем невозмущенный гравитационный потенциал на поверхности. Тогда, после деления на гравитационную постоянную, получим
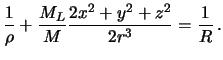
Здесь переменными величинами являются ![]() и
и ![]() .
Обозначим отношение масс
гравитирующего тела к массе планеты греческой буквой
.
Обозначим отношение масс
гравитирующего тела к массе планеты греческой буквой ![]() и решим полученное
выражение относительно
и решим полученное
выражение относительно ![]() :
:
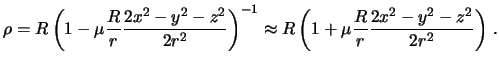
Так как
![]() , с той же степенью точности
получим
, с той же степенью точности
получим
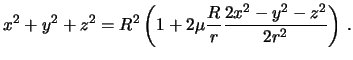
Преобразуем полученное выражение
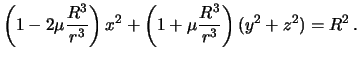
Учитывая, что отношения ![]() -- малые величины последнее выражение можно
переписать так
-- малые величины последнее выражение можно
переписать так
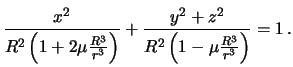
Мы получили уравнение двухосного эллипсоида, у которого ось вращения
совпадает с осью ![]() , то есть с прямой, соединяющей притягивающее тело с центром
Земли. Полуоси этого эллипсоида, очевидно, равны
, то есть с прямой, соединяющей притягивающее тело с центром
Земли. Полуоси этого эллипсоида, очевидно, равны
Итак, уровенная поверхность, заданная в виде шара, вследствие приливного
действия другого небесного тела вытягивается в сторону этого тела и
превращается в эллипсоид вращения. Большая полуось будет превышать радиус
планеты на величину
![]() , а малые полуоси будут меньше радиуса на величину
, а малые полуоси будут меньше радиуса на величину
![]() .
Заметим, кстати, что с той же степенью точности произведение всех трех
полуосей остаются постоянными, что говорит о неизменности объема,
ограниченного поверхностью уровня.
.
Заметим, кстати, что с той же степенью точности произведение всех трех
полуосей остаются постоянными, что говорит о неизменности объема,
ограниченного поверхностью уровня.
Для иллюстрации сказанного приведем численный пример. Вычислим приливной
"горб" на Земле, вызванный притяжением Луны. Радиус Земли равен
![]() = 6378 км,
расстояние между центрами Земли и Луны равно
= 6378 км,
расстояние между центрами Земли и Луны равно
![]() км,
отношение масс Луна/Земля равно 1:81. Подставляя эти данные в формулу для
увеличения большой полуоси, получим 0,36 м Нетрудно подсчитать, что на Луне
аналогичный приливной горб, направленный в сторону Земли будет равен 13 м.
км,
отношение масс Луна/Земля равно 1:81. Подставляя эти данные в формулу для
увеличения большой полуоси, получим 0,36 м Нетрудно подсчитать, что на Луне
аналогичный приливной горб, направленный в сторону Земли будет равен 13 м.
Необходимо подчеркнуть, что в приведенных рассуждениях не учитывается приливные деформации самой Земли, что также изменит поверхность уровня. Для строгих выкладок необходимо задать модель Земли, ее строение, упругие постоянные и т.п., что, конечно, выходит далеко за рамки нашего курса.
6.1.2 Преобразование формулы для приливообразующего потенциала
Вернемся к формуле (6.10). Здесь аргументом полиномов Лежандра является
геоцентрическое зенитное расстояние притягивающего небесного тела ![]() .
Рассмотрим треугольник OPL. Сторона ОР,
как мы знаем, равна радиусу Земного шара
.
Рассмотрим треугольник OPL. Сторона ОР,
как мы знаем, равна радиусу Земного шара
![]() (если точка P находится на поверхности земного
шара), сторона OL равна расстоянию между центрами масс притягивающего и
притягиваемого тела
(если точка P находится на поверхности земного
шара), сторона OL равна расстоянию между центрами масс притягивающего и
притягиваемого тела ![]() , угол между этими сторонами равен геоцентрическому
зенитному расстоянию
, угол между этими сторонами равен геоцентрическому
зенитному расстоянию ![]() , угол между сторонами PL
и продолжением стороны ОР равен
зенитному расстоянию z. Проекция стороны OL на продолжение стороны
ОР равна
, угол между сторонами PL
и продолжением стороны ОР равен
зенитному расстоянию z. Проекция стороны OL на продолжение стороны
ОР равна
![]() . Отсюда
. Отсюда
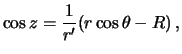
Можно ли заменить геоцентрическое зенитное расстояние топоцентрическим,
которое используется в астрономии? Какую ошибку мы сделаем, если заменим в
формуле (6.8) угол ![]() зенитным расстоянием
зенитным расстоянием ![]() ? Очевидно, что мы должны оценить
величину
? Очевидно, что мы должны оценить
величину
![]()
Пусть отношение ![]() является малой величиной, тогда
является малой величиной, тогда
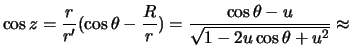
следовательно
![]() . Эта величина максимальна при
. Эта величина максимальна при
![]() .
Так если гравитирующее тело --
Луна, то
.
Так если гравитирующее тело --
Луна, то ![]() =6.371/384.4=0.0166. Следовательно, максимальное искажение
зенитного расстояния в системе Земля-Луна не превосходит 1,7%. Для
большинства задач этим отличием можно пренебречь и в качестве
приливообразующего потенциала брать
=6.371/384.4=0.0166. Следовательно, максимальное искажение
зенитного расстояния в системе Земля-Луна не превосходит 1,7%. Для
большинства задач этим отличием можно пренебречь и в качестве
приливообразующего потенциала брать
Понятно, что наибольший вклад в приливные явления создает первый член формулы (6.10). Очень часто им и ограничиваются, хотя при строгом анализе приливных явлений приходится учитывать и остальные члены разложения (6.10).
Итак, приливообразующий потенциал с точностью до
![]() имеет вид
имеет вид
Выполним некоторые преобразования полученной формулы и приведем к
общепринятому виду. Поскольку
![]() ,
то подставляя это выражение в формулу (6.11) осле несложных преобразований,
получим
,
то подставляя это выражение в формулу (6.11) осле несложных преобразований,
получим
Величина
![]() называется постоянной Дудсона.
Теперь вместо (6.12) можно
записать
называется постоянной Дудсона.
Теперь вместо (6.12) можно
записать
Заметим, что так называемая постоянная Дудсона вовсе не является, постоянной величиной, так как расстояние между притягивающим и притягиваемым телами изменяются из-за того что они движутся по орбитам, строго говоря, не эллиптическим, подчиняясь законам небесной механики. В книге бельгийского ученого П. Мельхиора известного специалиста по приливам приводятся численные значения постоянных Дудсона:
| для Луны | |
| для Солнца |
<< 5.2 Температура в недрах | Оглавление | 6.2 Типы приливных волн >>
|
Публикации с ключевыми словами:
гравиметрия - геофизика - солнечная система - сейсмология
Публикации со словами: гравиметрия - геофизика - солнечная система - сейсмология | |
См. также:
Все публикации на ту же тему >> | |