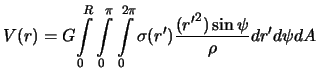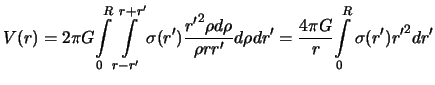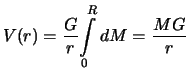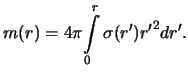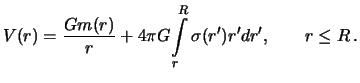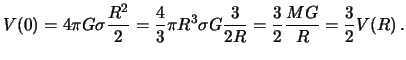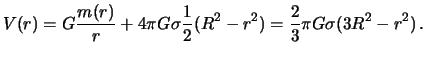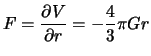по текстам   по ключевым словам   в глоссарии   по сайтам   перевод

Разделы

• 3.3.1 Потенциал шара во внутренней точке
• 3.3.2 Гравитационный потенциал однородного шара

3.3 Гравитационный потенциал шара

Все планеты Солнечной системы имеют сферическую форму. Поэтому имеет смысл определить гравитационный потенциал шара. Для упрощения задачи, мы будем предполагать, что плотность шара зависит только от расстояния до его центра Нетрудно убедиться, что такой шар притягивает точно так же, как и материальная точка с массой равной массе шара и помещенная в его центр. Чтобы в этом убедиться, необходимо для формулы (3.4) выбрать такую систему координат, с помощью которой было бы удобно выполнять интегрирование.

Для начала, представим себе, что точка находится вне шара. Соединим эту точку с центром шара (точка О), полученный радиус-вектор обозначим через . Радиус-вектор элемента массы будем обозначать буквой . Следовательно расстояние между элементом массы и точкой , которое мы обозначили греческой буквой , будет иметь вид , где -- угол с вершиной в центре шара, образованный радиус-векторами и . Наконец, элемент массы определяется произведением плотности на объем элементарно малого параллелепипеда со сторонами , , и . Здесь мы ввели еще одну степень свободы -- поворот вокруг оси на угол . Таким образом,

Теперь вместо формулы (3.4) записать

(3.5)

Заменим переменную интегрирования на . Определим пределы интегрирования. Очевидно, что вместо 0 и нужно взять и , а . Переменную подынтегральное выражение не содержит, поэтому внутренний интеграл легко берется. Вместо (3.5) теперь будем иметь

(3.6)

Нетрудно догадаться, что есть масса бесконечно тонкой сферы , поэтому

(3.7)

Таким образом, мы пришли к очень важному выводу: шар со сферически симметрично распределенной массой притягивает так же, как и материальная точка с массой равной массе шара и помещенной в его центре.

3.3.1 Потенциал шара во внутренней точке

Рассмотрим сначала бесконечно тонкий шаровой слой с внутренней полостью, не содержащей массы. Тогда можно доказать, что внутри этой полости потенциал (силовая функция) есть постоянная величина, то есть этот шаровой слой внутреннюю точку не притягивает. Обратимся к рисунку. Через точку проведем коническую поверхность с вершиной в этой точке. Тогда эта поверхность вырежет на сферической поверхности элементарную площадку , а на другой стороне сферы -- элементарную площадку . Точка лежит под площадкой на расстоянии и испытывает со стороны этой площадки притяжение, равное , где -- коэффициент пропорциональности, зависящий от поверхностной плотности этого шара и от направления внешней нормали к площадке по отношению к радиусу-вектору точки . Элементарная площадка расположена на расстоянии от точки . Поскольку обе площадки видны из точки под одним и тем же телесным углом, то

Итак, обе силы равны и направлены в противоположные стороны. Теперь будем рассуждать следующим образом. Через точку Р проведем плоскость перпендикулярную радиус-вектору этой точки. Она разделит сферический "пузырь" на две части, назовем их условно верхнюю и нижнюю. Поскольку каждую из частей можно представить как бесконечную сумму элементарных площадок, то для каждой элементарной площадки верхней полусферы найдется симметричная ей площадка в нижней полусфере. Силы притяжения материальной точки, помещенной в точку , со стороны верхней и нижней полусфер равны и противоположны по направлению. Отсюда вывод: материальная точка, помещенная внутри полой сферы, этой сферой не притягивается

Рассуждения, приведенные здесь, нельзя считать строго математически обоснованными. Мы рассчитываем больше на интуицию, чем на строгую математическую логику. Однако, в теории потенциала притяжения математически строго доказано, что оболочка не притягивает материальную точку и в случае, когда эта оболочка имеет эллипсоидальную форму.

Мы показали, что гравитационный потенциал в полости, окруженной сферической поверхностью, является постоянной величиной. Однако, это имеет место лишь в том случае, когда эта полость притягивающих масс не содержит. Теперь откажемся от этого условия, и будем считать, что шар не полый, но плотность зависит только от расстояния до центра шара. Проведем через точку сферу так, что она разделит шар на внутренний шар с массой и шаровой слой с массой . Материальная точка будет притягиваться только внутренним шаром, так как шаровой слой, как мы видели, внутреннюю точку не притягивает. Поэтому гравитационная сила в точке направлена в центр шара и равна .

Знак "минус" мы поставили, чтобы подчеркнуть, что сила направлена в сторону, противоположную радиус-вектору. Массу внутреннего шара можно получить, интегрируя массу бесконечно тонкой сферы в пределах от 0 до

(3.8)

Поскольку , то для гравитационного потенциала во внутренней точке шара получим

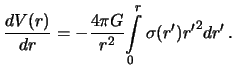
Интегрируя, будем иметь

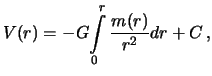
где С -- постоянная интегрирования. Полученное выражение можно проинтегрировать по частям. . Согласно формуле (3.8) : , поэтому 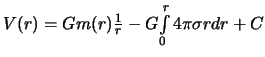. Определим теперь постоянную . Мы знаем, что , поэтому 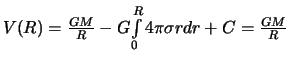. Следовательно .

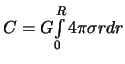Окончательно, формула для гравитационного потенциала во внутренней точке шара со сферически симметричной распределенной массой принимает вид

(3.9)

При переходе через поверхность потенциал сохраняет непрерывность. Очевидно, что при , будем иметь -- потенциал точки с массой, равной , расположенной в центре шара. В случае, когда точка находится в центре шара, то есть при , , а 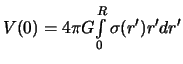, то эта величина зависит от закона изменения плотности с глубиной. В частности, если шар -- однородный, то его потенциал в центре шара равен

(3.10)

Отсюда следует вывод, что гравитационный потенциал в центре однородного шара в полтора раза больше, чем на его поверхности.

3.3.2 Гравитационный потенциал однородного шара

Гравитационный потенциал однородного шара во внешней точке ничем не отличается от потенциала шара, со сферически симметричным распределением массы, поэтому мы этот случай рассматривать не будем. Гравитационный потенциал однородного шара во внутренней точке может быть вычислен по формуле (3.9), в которой нужно положить плотность постоянной величине. Имеем

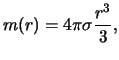
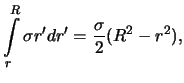
следовательно

(3.11)

В центре шара ()      -- значение, совпадающее с приведенным значением в формуле (3.10). На его поверхности .

Определим силу притяжения во внутренней точке:

(3.12)

Таким образом: сила притяжения внутренней материальной точки со стороны масс сферического тела линейно растет по абсолютной величине с расстоянием от центра шара и направлена к его центру. Другими словами, закон Ньютона, или, как еще его называют, закон обратных квадратов, превращается в закон Гука -- закон прямой пропорциональности "упругой" силы от величины отклонения тела от положения равновесия.

Нужно отметить, что если равномерно распределенная притягивающая масса занимает объем, ограниченный эллипсоидальной поверхностью, то и в этом случае вместо закона Ньютона следует брать закон Гука.

Покажем теперь, что во внутренней точке гравитационный потенциал подчиняется закону Пуассона: , где -- плотность вещества в точке .

Будем считать, что мы имеем дело с произвольным телом, ограниченным замкнутой поверхностью . Выделим внутри него фиксированную точку и окружим ее сферой с очень маленьким радиусом, с тем, чтобы плотность малой сферы считать постоянной величиной. Пусть -- потенциал всех масс тела в точке за исключением малой сферы, -- потенциал малой сферы, тогда . Потенциал удовлетворяет уравнению Лапласа, так как точка является внешней по отношению к рассматриваемой области, а для потенциала во внутренней точке однородного малого шара мы получили

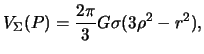
где -- радиус малой сферы. Определим оператор Лапласа для гравитационного потенциала в точке . Учитывая сказанное выше, будем иметь

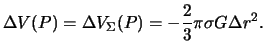
Поскольку , то , следовательно , а это и есть уравнение Пуассона.

При переходе точки через поверхность, где плотность изменяется скачком, изменится скачкообразно и правая часть уравнения Пуассона, левая часть которого представляет собой сумму вторых производных. Отсюда следует и разрыв непрерывности вторых производных гравитационного потенциала.

Версия для печати