 |
Астронет: И. И. Паша Волновые теории спиральной структуры галактик в 1960-е годы. I. http://variable-stars.ru/db/msg/1183369/pasha2.html |
II. ON A NEW WAVE CREST
| During a time when it was fashionable to "explain" the maintenance of spiral structure by magnetic fields, Lindblad persisted in the belief that gravitation was the dominant factor, and now we have come full circle back to this view. |
| E.M. Burbidge 1971, p.266 |
2.1 Regenerative spirals by Lynden-Bell
| We deduce that our galaxy is likely to have had spiral arms for most of its lifetime and that as old arms coil up so new uncoiled arms must start to form from their corpses. The problem of describing such a mechanisms we call the regeneration problem. |
| Lynden-Bell 1960b |
In 1960 Lynden-Bell presented at the University of Cambridge his PhD thesis "Stellar and Galactic Dynamics" (Lynden-Bell 1960b) 37 considering some general aspects of stellar-dynamical and ergodic theories. Its separate part "Cosmogonical gas dynamics" was on the spiral problem. It stated, echoing the stress of the day, that "the arms are primarily the seat of gas and dust" (so that the lenticular galaxies, deprived of them, "can no longer give birth to a spiral structure"). It found the cosmogonical approach the most convenient - in case of full denial from Jeans' classic scheme as inoperable in the presence of differential rotation.
"It seems impossible that the protogalactic gas was uniformly rotating when the stars formed. It seems more likely that as the primordial gas broke up into condensations [protogalaxies] each fluid element tended to preserve its angular momentum about the centre of the local condensation. The equilibrium reached is then one in which centrifugal force nearly balances gravity and the pressure is mainly important in preventing the system from becoming very flat."
Lynden-Bell analyzed realistic equilibrium configurations of a frictionless gas system and derived "an energy principle which should provide a powerful means of determining the equilibria on a computer". Any such configuration, when achieved by the system, is exposed to a slow secular evolution that "will not be determined by shrinkage due to the radiation of energy as in Jeans case, but by the transfer of angular momentum due to friction" neglected in the equilibrium derivations. The system "must: i) concentrate its angular momentum into a very small fraction of its total mass, and ii) leave the remainder a more concentrated uniformly rotating or pressure supported body. This is borne out by observation on both the scale of the solar system and that of the galaxy. [...] We should thus expect a uniformly rotating central condensation surrounded by a differentially rotating disc" (Lynden-Bell 1960b).
It is with such an evolved disk of gas that Lynden-Bell linked his spiral considerations. In shearing deformation - a point-blank menace to `any structural irregularity' - he, unlike many workers of the day, saw not an antagonist to the persistence of spiral arms, but a factor of their cyclic regeneration created through gravitational instability of the gaseous subsystem in a combined star-gas galactic disk (the stellar component being liable for gas equilibrium rather than for any collective dynamics). In such a setting, the problem needed a global stability analysis of a system in differential rotation, which technically was not feasible. That is why for want of the better Lynden-Bell employed the methods that had served Fricke (1954) with his = const model; this led to a necessary and sufficient condition of Jeans' stability, 2 / G 0 > 2/3 (cf. Sect. 1.3), and instructed the growth rate for unstable stages to be 2. An m = 2 mode at k 1/3 kpc-1 was found the most important, it fell down towards the disk edge and center, being long-wave and therefore fast-growing. This was in substance Lindblad's bar mode, one specified by a pair of condensations placed oppositely at r 9 kpc from the center. Before density had grown by a factor e, rotation turned the system through 180° (at = 2). But as this passed, effects of shear (excluded from the strict stability analysis) just wound the "azimuthally independent structure" round the galaxy, at least once. This meant a grave radial-wavelength reduction, which was expected to be a cause for slowing down the growth rate as effectively as to turn off instability altogether. In this event, the spiral arms would expand back "to form the sheet from which we started", and the whole process might then recur. However, a more careful analysis confirmed the dependence of on k only "for systems very close to stability". This would be "far too sensitive to give the great variety of spirals" and could not apply "for any part of the observed spiral arms". The regeneration theory proposed, Lynden-Bell (1960b) concluded, was "therefore untenable".
But as it turned out later, this pessimism was rather excessive, since it became clear eventually that there was a good deal of wisdom even in such regenerative thoughts. This, however, is not how things developed immediately, because, as we will see in the forthcoming section, the old idea of steady spiral modes was about to gain a new and important burst of enthusiasm.
Chia Ch'iao Lin was not an astronomer. Since the pre-war time, he had been studying fluid flows. By the 1960s, he had had over 60 publications, a monograph on hydrodynamic stability (Lin 1955), a world recognition of an applied science expert, and a solid reputation at the department of mathematics in the Massachusetts Institute of Technology (MIT) where he worked since 1947. But he did feel a continual interest in astronomy, being admired with strict analytical papers by Chandrasekhar, with M. Schwarzschild' work on stellar structure, with Zwicky's morphological method. In 1961 this side interest became Lin's life-long vitality. That spring, on visit in Princeton, 38 he attended the aforementioned conference on interstellar matter and, having become familiar with the developments in galaxy research, he got captured by the problem of the persistent spiral structure. 39
Back in MIT, Lin conveyed his galactic enthusiasm to his young colleagues Hunter and Toomre. 40 For quick acquaintance with current periodicals, a `reading group' was formed; 41 a "friendly back-and-forth atmosphere" (Toomre) warmed open discussions and working visits of Woltjer and Lust, organized by Lin; 42 Lebovitz was hired in the department. 43 In 1962, Shu arrived there for doing his undergraduate course work under Lin's guidance, 44 and Hunter with Toomre, their instructorship finished, left MIT, one back for Cambridge, UK, the other for Princeton; their first papers appeared in 1963.
Hunter and Toomre made their debut in galaxy dynamics on a vital problem already posed but yet unanswered very basically (Kuzmin 1956; Burbidge et al 1959): How to connect the empirical rotation curves of galaxies with their equilibrium mass distribution? Toomre (1963) set forth a general mathematical method, and for a razor-thin disk model he derived a series of solutions well known nowadays as Toomre's models of nth order (Binney & Tremaine 1987, p.44). 45 Hunter (1963) used a distinct thin-disk approximation and found another series of exact solutions. The simplest there was the case of uniform rotation and surface density µ0(r) (1 - r2 / R2)1/2. For it only was the analytical study of equilibrium stability possible, and Hunter did it "using only pencil, paper, and Legendre polynomials" (Toomre 1977, p.464). This cold disk proved unstable for a wide span of axisymmetric and non-axisymmetric oscillation modes. 46 These papers by Toomre and Hunter had paved the way for further works on kinematical models and global dynamics of flat stellar systems.
2.3. Gravitational stability of flat systems
| Lin asked [Woltjer in 1961]: What are the circumstances that would be needed for either one or both of the stellar and inter- stellar parts of a supposedly smooth galactic disk to remain gravitationally stable against all large scale disturbances? |
| Toomre 1964, p.1217 |
| The importance of collective effects in our Galaxy was first clearly pointed out by Toomre (1964). He showed that in the disk the stellar motions are sufficiently coherent to make it almost vulnerable to collapse. He also pointed out that the scale on which this would occur is quite large. |
| Kalnajs 1971, p.275 |
As we have seen, Safronov already raised the question of gravitational instability in flat rotating systems, aiming at the breakup of a protoplanetary cloud into detached rings. Toomre, interested in basically smoother objects like galaxies, turned in 1961 to a rather close, although opposite in accent, topic, and by the summer of 1963 he prepared an article "On the gravitational stability of a disk of stars" (Toomre 1964, hereinafter T64).
The paper started with the general presentation of the problem as it was then seen.
"The well-known instabilities of those Maclaurin spheroids whose rotational flattening exceeds a certain fairly moderate value suggest that the other sufficiently flattened, rotating, and self-gravitating systems might in some sense likewise be unstable. At any rate, these instabilities have been often cited as a likely reason why one does not observe elliptical galaxies exceeding a certain degree of oblateness. It is only when we turn to consider what are now thought to be the distributions of all but the youngest stars in the disks of the ordinary (as opposed to the barred) spiral galaxies that this classical result suggests a serious dilemma: How is it conceivable, in spite of these or analogous instabilities, that so much of the fainter stellar matter within such galaxies - and certainly the S0 galaxies - should today appear distributed relatively evenly over disks with something like a ten-to-one flattening?" (T64, p.1217)
The detailed study of the problem was preceded by a primary, qualitative stability estimate.
A rotating thin cold disk, in an approximate equilibrium between gravity and centrifugal forces acting on each mass element, is prevented from general contraction, still not from fragmentation. Small-size clumpings arise everywhere in such a disk, and then collapse, their gravity taking excess over rotation. But if larger-sized, they do not go as these two factors counteract each other. The demarcation length scale LT proves plain co-measurable with the disk radius R. Thus the cold model, for all specifications it may have, is clearly unstable. 47 The part played by random motions is best visualized with an immovable sheet model. There instability is avoided if stars (other mass elements), having an rms velocity ñ, cross a clumping zone in a time not exceeding that needed for an e -fold amplitude growth as registered in the cold case. Hence the largest yet ungrowing disturbance is found on an LJ c2 / Gµ0 scale, which is essentially the Jeans stability criterion. Now, letting the sheet rotate, one sees the two characteristic scales, LT and LJ, be present (Fig.5). LJ gets closer to LT for higher velocity dispersions, until they coincide at c's as high - in the order of magnitude - as the rotational velocity, thus meaning full stabilization against this sort of disturbances.
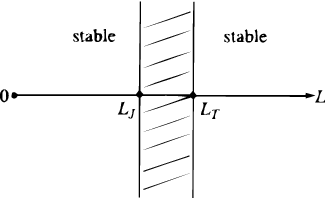 |
Figure 5. Characteristic scales in a gravitating disk. A cold rotating disk is stable for radial disturbances on the scales L > LT, a non-rotating hot disk is stable of scales L < LJ, a hot rotating disk is stable on both scales. As the velocity dispersion becomes of the order of the circular velocity, one obtains full axisymmetric stability. |
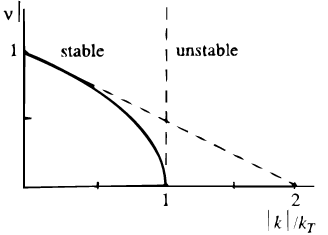
The strict analysis of axisymmetric disturbances to a razor-thin disk, performed in T64, supported these rough estimates. In the cold case, it led to a local dispersion relation
| (5a) |
or
| (5b) |
linking the wave frequency in units of , = / , with a critical wavenumber
| (6) |
the one to determine the shortest wavelength T 2 / kT of ungrowing (2 0) disturbances (Fig.6). 48 The hot-disk analysis detected the minimum radial velocity dispersion at which the system is still resistant against all axisymmetric disturbances (Fig.7): 49,50
| (7) |
The real-to-minimum velocity-dispersion ratio
| (8) |
thus got a local disk-stability parameter. 51,52 In a marginally stable state Q = 1, disturbances of 0 0.55 T proved most unpliant and barely suppressible. Our solar neighborhood would have such a 0 5 - 8 kpc, but if some Q 1 - 1.5 were not preferred empirically, implying a certain stability reserve. Of course, "it was as yet impossible to rule out instabilities altogether", but should any actually be present, they would not do with scales responding to the challenging 2-kpc spacings, as these "must almost certainly be judged as stable". This "is important as an argument against any suggestion that the existing spiral structure in this Galaxy might be the result of collective stellar instabilities" of the sort considered (T64, p.1236).
 |
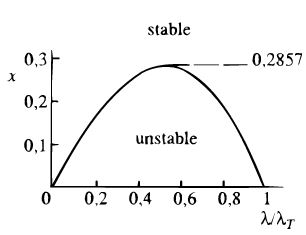 |
Figure 6. (left) The dispersion relation
curve for radial oscillations and tightly wrapped spiral waves in a
cold disk.
|
|
Still, the linear theory developed could not lay claim to very much. So it did not elucidate the cause of stellar disk heating, it even could not show any definitely what was to become with primary condensations appearing in a tentatively cold disk in one or two revolutions already. "It must not be presumed that such initial clumpings would necessarily have led to the formation of any permanent irregularities", Toomre noticed. "On the contrary, it seems much more likely that the bulk of the stars involved in any given (generally non-axisymmetric) instability [...] would eventually have dispersed themselves upon emerging from the opposite sides of the aggregation and upon experiencing the shearing effect of differential rotation".
"It follows that an initially unstable disk of stars should probably have undergone not just one but several successive generations of instabilities, after each of which the system would have been left somewhat less unstable than it was previously. In particular, it seems likely that before very many rotation periods had elapsed, the disk would have approached a new equilibrium state that was again fairly regular and quite possibly axisymmetric, but in which the random velocities at the various radii had become - and would henceforth remain - about equal to the minimum values needed for complete stability: (T64, p.1237)." 53
Besides, since the total gravitational energy of the disk would have had to be the same during its evolution (the virial theorem), "the said redistribution of stars could not simply have consisted of an overall contraction, but would have had to entail a contraction perhaps in the inner parts of the disk jointly with a net expansion of the outer portions" (T64, p.1237) - as it was already seen by Lynden-Bell (1960b) from the gas-dynamical viewpoint.
As regards non-axisymmetric disturbances, it was pointed out in T64 that because of the specific action of the Coriolis force those are restrained even more effectively than radial disturbances, thus requiring no addition for cr, min. However, Toomre remarked, a question that his discussion left "completely unanswered" was "to what extent a similar amount of random motion [Q = 1] might affect the character of the most extensive non-axisymmetric disturbances, in particular those which ought to determine whether or not a given disk might prefer to develop into a barlike structure" (T64, p.1235). 54
2.4. Kalnajs' search for spiral modes
| One can draw a parallel between the attempts to talk about galactic evolution at the present time and the attempts to understand stellar evolution before the sources of energy in the stars were understood. |
| G. R. Burbidge 1962, p.291 |
| The study of stellar systems, such as our own galaxy, is not limited by a lack of understanding of the underlying principles, but rather by the difficulty of solving the differential equations which govern the time evolution of the system. |
| Kalnajs 1962, p.i |
Agris Kalnajs began his undergraduate studies in Electrical Engineering at MIT in 1955. As a good student, he participated in a special course which emphasized physics and mathematics, and provided summer employment in the Microwave Research Lab at Raytheon, making measurements for computer modeling of magnetrons. There he learned about such things as electron motions in crossed electric and magnetic field, waves carrying positive and negative energies, modes, coupled modes, parametric amplification. All this proved to be really useful in a quite different field when he arrived in 1959 in the astronomy department at Harvard University and got involved in galaxy dynamics. 55
In the fall of 1961 Kalnajs made a research examination on "Stellar kinematics" (Kalnajs 1962). 56 The task was to calculate self-consistent radial oscillations in a rotating stellar disk as a tentative explanation for the `local' arms in our Galaxy. Their short spacing L 3 kpc justified the small-scale analysis in the plane of a homogeneous thin sheet. Kalnajs solved the Vlasov and Poisson equations as an initial-value problem and obtained an equation for the radial oscillations and a dispersion relation which was formally correct. 57 As he was interested in short waves, he made an asymptotic evaluation of the integral expression, and in the process left out "a factor 2 or something of that order" (Kalnajs). This and the reduced disk response at the short waves ( ~ 1 kpc) made him conclude that , because the self-gravity effects became "too small to be interesting" (Kalnajs): all the solutions oscillated and were traveling waves that, in passing, "tend to gather up the low dispersion objects such as gas" (Kalnajs 1962, p. ii). As a plausible "arm-like density wave" generator, an oval-shaped body at the Galaxy center was mentioned.
The error in this asymptotic evaluation was uncovered in the summer of 1963 when Kalnajs and Toomre finally got together, compared and crosschecked their notes, and detected each other's technical errors. Kalnajs looked anew at his radial-oscillation theory and re-evaluated the dispersion relation, this time into the form in which it entered his thesis (Kalnajs 1965). 58 In modern notation - whose convenience and clarity we owe undoubtedly to Lin - and without the uninteresting stellar disk thickness correction going through that original 1961-63 analysis, 59 it is
| (9) |
where
| (10) |
is Kalnajs' version of a factor to account for the role played by random motions of stars. There is no such play in the limit x = 0, relation (9) then reduces to Toomre's cold-disk result (5) that shows the gravity term proportional to the wavenumber and growing without bound. Now random motions arrest this growth: the total contribution of gravity only reaches a maximum at x0 1, still giving rise to instability (2 < 0) if large enough, and for x > > 1 it becomes small. In the solar neighborhood that value of x0 points to a radial wavelength 0 6 kpc, the one concluded by Toomre from his neutral stability analysis. Its commensurability with the radial size of the Galactic disk makes the local theory somewhat suspect.
"When I wrote my Research Examination I was under the impression that the spacing between the spiral arms was about 1.5 kpc. After Toomre and I got together, it became clear to me that the 1.5 kpc waves/fluctuations were not the important modes of the Galaxy. [...] Also by the fall of 1963 I had obtained my own copy of Danver's thesis (thanks to my uncle who was at Lund University). Danver had measured the spiral patterns and came up with a typical pitch angle of 16°.6. This implies scales even larger than 6 kpc. [...] By this time Alar had published his disk models, and I could use them to estimate the scales at which these disks were most responsive, and they convinced me that a WKBJ approach [see Sect. 3.1] was too crude [...] and that - unlike plasma - galaxies were too inhomogeneous. [...] So the future was `global modes and integral equations'." (Kalnajs)
Once he realized this fact, Kalnajs lost interest in the local theories, which were good for the stable small-scale solutions, and turned to global modes as the correct approach to the oscillation problem. In the fall of 1963 he presented to his thesis committee at Harvard "An outline of a thesis on the topic `Spiral structure in galaxies'" (Kalnajs 1963), summarizing his ideas for a new theory of steady spiral waves. Because this document has been almost unknown, a long quotation from it appears to be quite appropriate. 60
"A feature peculiar to highly flattened stellar systems is the appearance of spiral markings, called arms. These features are most prominently displayed by the gaseous component of the galaxy and the young hot stars which excite the gas. However, the density fluctuations can still be seen in the stellar component, appearing much fainter, but also more regular.
The division of the galaxy into two components, gaseous and stellar, appears natural when one considers the dynamical behavior of these two subsystems. The gaseous component is partly ionized and is therefore subject to magnetic as well as gravitational forces, and has a very uneven distribution in the galactic plane. The stellar system is quite regular, its dynamics being governed by the long-range gravitational forces arising from the galaxy as a whole; the density of stars is sufficiently low that binary encounters between stars may be ignored. The stellar component, which is the more massive, cannot support density fluctuations on a scale much smaller that the mean deviation of the stars from a circular orbit (or the scale of the peculiar motions). The gas, on the other hand, would support smaller-scale fluctuations - at least in the absence of magnetic effects. The fact that observed spiral arms are not much narrower than the smallest scale that the stars will tolerate suggests that stars must participate actively in the spiral patterns.
There is a fundamental difficulty, however, in the assumption that spiral arms are entirely stellar: if an arm can exist and does not grow in time, then its mirror image is also a possible configuration. This follows from the time-reversibility of the equations of motion combined with their invariance under spatial inversion. Thus the leading or trailing character cannot be decided on the basis of a linearized theory if we insist on permanency of the spiral markings. The observations indicate, however, that nature in fact prefers trailing spiral arms. Thus a plausible theory of spiral structure must include both the stars and the gas.
I regard the galaxy as consisting of two components, gas and stars, coupled by gravitational forces. The stars provide the large scale organization and the gas discriminates between leading and trailing arms. ([Footnote in the original text]: The stellar system can be thought of as a resonator, and the gas would then be the driver which excites certain of the normal modes.) If the coupling is not too strong, one may at first consider the two subsystems separately, and afterwards allow for their interaction. Unfortunately, one cannot evaluate the magnitude of the coupling without calculating the normal modes of the two subsystems. For the gaseous component, only the crudest type of analysis is possible at present, since one should include non-linear terms in the equations governing the gas motion in order to be realistic. The stellar component, on the other hand, is sufficiently smooth that a linearized theory should apply, and the problem of determining the normal modes can be formulated, and, with a little effort, solved.
I have chosen as my thesis topic the investigation of the stellar normal modes in the plane of a model galaxy. [...] Some qualitative features of the equations indicate that the type of spiral disturbance with two arms is preferred. This result does not seem to depend critically on the model, which is encouraging. The final proof has to be left to numerical calculations, which are not yet complete." (Kalnajs 1963, p.1-3)
It is seen therefore that Kalnajs was envisaging the disk of stars as a resonator in which global spiral-wave modes are developed. If stationary, the leading and the trailing components are just mirror-imaged, so that, superimposed, they give no spiral pattern. However, due to slow non-reversible processes occurring in real galaxies, the symmetry is violated.
In support of his normal-mode concept, Kalnajs considered large-scale non-axisymmetric disturbances to a hot inhomogeneous flat stellar disk, and derived for them a general integral equation whose complicated frequency dependence implied a discrete wave spectrum. He also pointed out the role of Lindblad's condition (4). When satisfied, large parts of the galactic disk could support coherent oscillations for the m = 2 mode, whereas for larger m's there would be Lindblad resonances within the disk. Stars in these regions feel the perturbing wave potential at their own natural frequency,
| (11) |
thus undergoing strong orbital displacement and making the m > 2 modes lose integrity 61 . Hence Kalnajs concluded that his "formulation of the problem" shows a dynamical preference for two-armed spirals and "gives little insight of what to expect in both the shape of the disturbances and their time dependence when m > 2" (Kalnajs 1963, p.13).
A summarizing exposition of the subject Kalnajs gave in his PhD thesis "The Stability of Highly Flattened Galaxies" presented at Harvard in May 1965 (Kalnajs 1965); 62 it contained an extended discussion lavish in ideas and technicalities. At the same time, the thesis became in fact Kalnajs' official public debut, so that to it as a reference point should we attach chronology when confronting certain factual points in the spiral history of the 1960s.
37 Leon Mestel was his advisor. Back.
38 Stromgren invited him for discussions on stellar structure (Lin), largely in relation to his fresh interest in hydrodynamics of liquid helium (Lin 1959). Back.
39 In his early spiral papers, Lin often quoted Oort's statement reproduced in Sect. 1.3. Back.
40 At that time, the department of mathematics in MIT was vigorously enlarging its applied side. Hunter and Toomre were hired there in 1960, just after they had got their PhD degrees in fluid dynamics in England. Initially, they hoped to collaborate with Backus (Hunter; Toomre), a recognized leader in geomagnetic problems, but as he left MIT that year already, they two "soon caught some of Lin's fever for problems in the dynamics of galaxies". "Almost at the moment I first met him in fall 1960 I was struck with his breadth of scientific interests, his really excellent spoken English, [...] and his genuinely gracious manner of dealing with other people". (Toomre) Back.
41 "[We] were all becoming interested in astrophysical problems together. We read Martin Schwarzschild's book on stellar structure together". (Hunter) Back.
42 "It was a real pleasure to have such a thoughtful and articulate theoretical astrophysicist as Woltjer so close to chat with about this thing or that. [...] It was from his informal lectures that summer that I learned for the first time not only how Dutch and Australian radio astronomers working in parallel had more or less mapped the spiral arms of this Galaxy from the velocity maps, but also how astonishingly thin - and yet curiously bent - is our layer of 21-cm gas". (Toomre) Back.
43 "I had just received my PhD [working with Chandrasekhar], I wished to pursue applied mathematics, and I had received an offer of an instructorship from one of the best applied-mathematics departments in the country. Lin's motive I can only speculate on. He was interested in moving in the direction of astronomy and of the spiral-structure problem and perhaps figured I would be a useful participant. If this is the case, I suppose my stay at MIT may have been somewhat disappointing to him because I spent all of it in close collaboration with Chandrasekhar on a quite different set of problems". (Lebovitz) Back.
44 "I began work with C.C. Lin in summer 1962 as an undergraduate research assistant and continued through the fall and spring 1963, on the topic of spiral structure in galaxies as my undergraduate thesis project in physics at MIT [...] I knew Lin from even earlier because he is a close friend of my father". (Shu) Back.
45 Toomre's model 1 reproduced the result by Kuzmin (1956) then unknown to Toomre (Binney & Tremaine 1987, p.43). Back.
46 The stability of differentially rotating cold disks Hunter studied in his subsequent paper (Hunter 1965). Back.
47 Toomre got this estimate by the fall of 1961 and was struck with the fact that nothing had ever been said on the thing just shocking with its as simply derivable inference that cold disks be prone to violent instabilities. (Toomre) Back.
48 Analyzing axisymmetric disturbances to a flattened rotating cloud, Safronov (1960a, b) did not solve the Poisson equation. He was guided by the notice that short radial waves find adequate the cylindric approximation for a torus (ring). But the cylinder is the sum of `rods', or elementary cylinders whose individual gravity is given by a simple formula, so that the business is just to integrate in infinite limits the elementary contributions over longitudal and transversal variables xand z. There Safronov was not perfect, however. His gently stratified cloud turned a stiff 2h -thick plate as he took his introduced density function 0(z) out of integration over z. His subsequent integration over xwas in an interval of ± /4; that, he argued, ensured a predominant contribution to the perturbed force (which is qualitatively true). Had he integrated in infinite limits, and first - most trivially - over x, the gravity term in his Eqn (3) would have become -2 Gk 0(z / h)e-k|z| dz, and with the exponential factor serving as a thickness correction he would have accurately managed with any density profile - and, most obviously, would have found that in the zero-thickness limit that factor simplifies to unity, the integral just gives the surface density µ0, so that the gravity term converts into - 2 G µ0 k, the form in which it was presented soon by Toomre (1964) in frames of `regular' methods of the potential theory. Back.
49 To solve the Vlasov kinetic equation, Toomre used the characteristics method that for some three-dimensional purposes had already served Lynden-Bell (1962), who in his turn cited the original source (Bernstein 1958) where that method had genuinely helped with the general disperion relation for the mathematically similar problem with a Maxwellian plasma in a magnetic field. Back.
50 Because of a technical error in Toomre's analysis, this minimum value was initially overestimated by 20%. Not so little if one considers that the difference in cr, min for star and gas disk models (the latter case admits a much simpler analysis) reaches 7% only. It is this "substantial error" which was detected in 1963 by Kalnajs (cf. Sect. 2.4), as reported frankly in T64 (p.1233). Back.
51 Formally, the `Q -parameter' (8) was introduced by Julian and Toomre (1966). Back.
52 This quantitative analysis refines the above view of disk stabilization as it shows via Eqs (6) and (7) that locally the result is attained already once LJ / LT = (3.36/2 )2 0.286 (0.25 in a gas disk). Back.
53 Asked to reminisce on how he had originally understood those dispersion velocities "about equal" to the needed minimum in the new equilibrium state - on whether or not this was a factual suggestion of marginal stability of our stellar disk, or some extra amount was yet permitted for its stability - Toomre has responded: "It is hard for me to reconstruct from this vantage point what exactly I meant or hoped by that statement. Probably I was mostly just trying to rationalize the surprising fact which I had then unearthed that the minimum theoretically needed cr, min and the observed amounts seemed to agree so well within their considerable uncertainties, meaning within a factor of 1.5 or thereabouts, rather than some 2 or 3 or 4 [...] From about 1966 onwards, I was surely of the opinion that any Q less than about 1.5 here was highly suspect, if not downright ludicrous, because of fierce heating of cooler disks by their embedded gas complexes. But that came a little later. In 1964 my views were no doubt more permissive toward Q = 1.0". (Toomre) Back.
54 Real progress in the study of this problem first came half a decade later. Back.
55 "It was probably David Layzer's course in classical dynamics which steered me towards stellar dynamics. I rather liked David's approach: he strived for elegance. He put a lot of thought in his lectures". (Kalnajs) Back.
56 As this was only an unpublished internal document, its outline below is mainly to illustrate how Kalnajs was then progressing. Back.
57 Following Landau's method correctly describing small oscillations in homogeneous electrostatic plasma, an arbitrary disturbance is initially imposed on the stellar sheet and its evolution is traced out. With time, the dependence on the initial conditions dies away, and the result is provided by the integrand poles whose expression - the dispersion relation - connects the established wave parameters. Back.
58 "Strictly speaking, I was the first to write down the dispersion relation. But that is not the important thing. What is more important is who made the best use of that equation. And here it was Toomre, who used it to discuss the stability of the Galactic disk - a distinctly more fundamental topic than the subject of my Research Examination. [... ] By the time we got together in 1963, that is probably the way we understood our respective contributions". (Kalnajs) Back.
59 The thickness corrections were worth considering for wavelengths as short as 1.5 kpc as they reduced the radial force by a factor of 2 or 3, but for 6 kpc the reduction was some 20%-30% at most. Back.
60 "I do not recall exactly when I first learned that Lin was also interested in spiral density waves (it was probably a talk he gave at MIT), but at that stage our relations were most cordial and I also felt that my understanding of this topic was more thorough than his. So having produced a written document, I am pretty sure that I would have found it difficult not to boast about my achievements" (Kalnajs). "A written document" there refers to the "Outline" which at least Toomre received from Kalnajs in November 1963. Back.
61 A combination - m is called the Doppler-shifted wave frequency, one reckoned in a reference system corotating with disk material. The shift is due to the fact that waves are naturally carried along by flows. Back.
62 Kalnajs' thesis committee members were Layzer, Lin and Toomre, as officially confirmed from Harvard. Back.
<< 1. Lindblad's Era | Contents | 3. The Lin-Shu Theory >>