Астронет > Как на самом деле выглядит черная дыра?

Астронет: М. Е. Прохоров/ГАИШ Как на самом деле выглядит черная дыра?
http://variable-stars.ru/db/msg/1176653

Как на самом деле выглядит черная дыра?
7.05.2002 20:02 | М. Е. Прохоров/ГАИШ, Москва

Наверное я не совсем точно сформулировал свой вопрос - то о чем пойдет речь нельзя увидеть не только глазом, но и в телескоп (даже в рентгеновский или радио). Но воображаемые вещи - наше представление о предмете - не менее реально, чем то, что мы наблюдаем.

Речь пойдет о "форме" черной дыры, причем черной дыры вращающейся (или Керровской - по имени Керра, того кто первым вывел математическое описание таких дыр).

В 1963 году математик из Новой Зеландии Рой Керр (Roy Kerr) получил точное (аналитическое) решение для вращающейся черной дыры. [Фото 1975 года.]

Невращающиеся черные дыры тоже имеют сложную внутреннюю структуру (см. описание решения Шварцшильда и решения для черной дыры с электрическим зарядом (черная дыра Райснера-Нордстрема)), но форма всех их поверхностей может быть только сферической.

Рис. 1. Классическое изображение вращающейся черной дыры (см., например, книгу У.Кауфмана).

Если вы уже интересовались черными дырами или Общей теорией относительности, то вам уже могла встречаться картинка, показанная на рис.1. На ней показаны в разрезе две поверхности. Сферическая - это горизонт черной дыры. Ни одна материальная частица, даже фотоны, не могут выйти из под горизонта, все они падают к центру черной дыры. А сплюснутая поверхность называется эргосферой, частицы внутри нее могут удержаться от падения в черную дыру, но обязаны вращаться вместе с ней (в том же направлении, что и черная дыра, но с различными скоростями, зависящими от положения частицы в эргосфере). Эти две поверхности касаются друг друга на полюсах черной дыры, т.е. на оси ее вращения, а на экваторе размеры эргосферы больше, чем у горизонта. Таким интересным образом во вращающихся черных дырах проявляются "центробежные силы". [Подробнее о свойствах вращающихся черных дыр можно прочитать в соответствующей главе книги Кауфмана.]

Обращаем ваше внимание, что показанные на рис.1 поверхности касаются друг друга гладким образом, что в общем-то не удивительно, поскольку по форме эргосфера похожа на сплюснутый эллипсоид.

Так вот - это не верно!

Самые нетерпеливые могут посмотреть на рис.3, а для остальных мы объясним все подробнее.

Математические исследования геометрии черных дыр показали, что двумерная поверхность эргосферы вблизи полюсов обладает коническими особенностями. Что это означает? Окружность радиуса r - это кривая, каждая точка которой находится от ее центра (точки О) на расстоянии r. Если окружность нарисована на плоскости (что мы обычно и видим), то отношение ее длины l к радиусу r будет равно

$\ell/r = 2\pi\,.$

Но окружности можно рисовать и на кривых поверхностях, тогда отношение ее длины и радиуса (который отсчитывается вдоль поверхности) будет отличаться от $2\pi$ . Однако любая гладкая поверхность, если рассматривать ее в небольших масштабах, становится все более и более похожей на плоскость. (Здесь можно привести много примеров из математики, геометрии и, даже, космологии, но я не буду этого делать.) Математически это выражается так:

для гладкой поверхности $\ell/r \to 2\pi$ при $r \to 0$ .

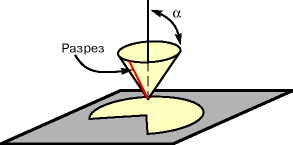Рис. 2. Иллюстрация уменьшения длины окружности на конической поверхности.

Этот вывод нарушается, если поверхность не является гладкой и вы рисуете окружность именно вокруг особой точки. Самый известный пример такой поверхности - конус (а особая точка, конечно, его вершина). На конусе с углом полураствора $\alpha$ отношение длины окружности к радиусу равно $\ell/r = 2\pi\sin\alpha$ , т.е. она всегда меньше $2\pi$ . Такой вывод легко можно сделать и по-другому, если разрезать конус по образующей (как показано на рис.2), то он без разрывов и растяжения разворачивается на плоскость в которой будет не хватать сектора (как в пироге их которого уже отрезали кусок). Соответственно и длина окружности окажется меньше. Обращаю ваше внимание, что этот разрез сделали мы с вами для того, чтобы развернуть поверхность конуса на плоскость. Его можно было провести и в любом другом тесте, так как на самом конусе никаких особенностей не было.

Рис. 3. Классическое изображение вращающейся черной дыры (см., например, книгу У.Кауфмана).

Именно такие конические особенности геометрии были обнаружены вблизи полюсов эргосферы Керровской черной дыры. А для того, чтобы их "увидеть", эти поверхности (эргосферу и горизонт) вложили в плоское Евклидово пространство. (Что это такое? Как это было сделано? Всегда ли такое вложение возможно? Ответ на эти вопросы вы сможете найти в оригинальной статье gr-qc/0012052. К сожалению она на английском.) Результат такого вложения показан на рис.3. Как видите, эргосфера по прежнему касается горизонта на полюсах, но это касание не гладкое, а скорее напоминает прикосновение кончика авторучки к бумаге.

Для особо интересующихся скажу, что прежний рис.1 не содержит никакой математической ошибки, просто он нарисован в "очень кривой системе координат" (а общая теория относительности имеет дело в основном именно с такими искривленными пространствами), которая "замаскировала" конические особенности у полюсов.

Автор приносит огромную благодарность Дипаку Баскарану, обратившему мое внимание на работу Палеваса и др. (gr-qc/0012052), и за многочисленные последующие разъяснения.

[Иллюстрация в заголовке статьи показывает геометрию керровской черной дыры, возмущенную падающей на нее гравитационной волной. Изображение взято с сайта "International Art & Science" (http://www.i-a-s.de/). ]