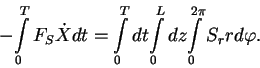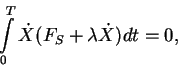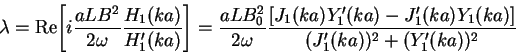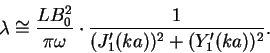 |
Астронет: А. А. Соловьев, Б. Б. Михаляев, Е. А. Киричек/Коуровка Радиационное затухание колебаний корональных петель http://variable-stars.ru/db/msg/1176579/node5.html |
<< 3. Радиационное затухание колебаний | Оглавление | 5. Заключение >>
4. Сила реакции излучения. Затухающие колебания корональной петли
На основе полученных выше результатов мы можем вычислить силу реакции
излучения 
и записать более реалистическое уравнение движения петли
с учетом радиационного затухания. Указанная сила определяется так, чтобы
работа, совершенная ею за период, была равна потери энергии на излучение за
тот же промежуток времени:
действует в направлении,
противоположном скорости. Рассмотрим поверхность цилиндра радиуса
а. Подставляя в (3) выражение для 
из
(1), получим:
Отсюда, с точностью до членов порядка 
, получаем
где
Здесь 
вычисляется через значение функций Бесселя при r =
a.
Используя приведенный выше вронскиан (2), а затем асимптотики (27), получим:
Уравнение колебаний петли с учетом радиационных потерь примет вид:
(сравни с
формулой (3)).
Решение для затухающих колебаний:
- амплитуда
колебаний, 
- начальная фаза,
- обратное
время затухания, условная
циклическая частота
Декремент затухания
колебаний равен
а
добротность
колебательной
системы -
Подставляя в
последнюю
формулу
выражения для К и
(при
), мы
снова придем к
формуле (29).
Время релаксации процесса составит:
Используя найденное выше численное значение
для добротности (Q = 8.76), получим: 
минут.
Это означает, что энергия первоначального толчка рассеивается волнами
(уменьшается в е раз ) всего за 3 периода колебаний, а время
релаксации составляет 12 минут, что очень хорошо соответствует имеющимся
наблюдательным данным (в примере, обсуждаемом в [4], для времени
релаксации получено 14.5
2.7 минут).
<< 3. Радиационное затухание колебаний | Оглавление | 5. Заключение >>