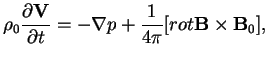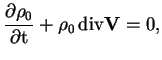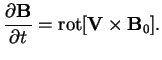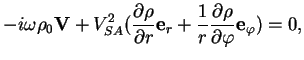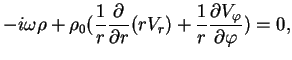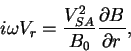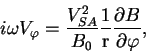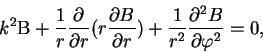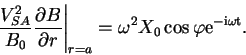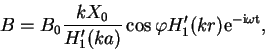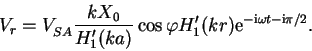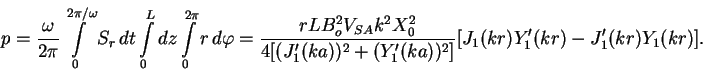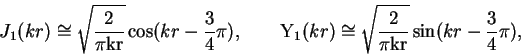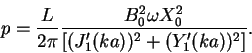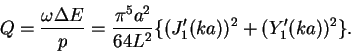 |
Астронет: А. А. Соловьев, Б. Б. Михаляев, Е. А. Киричек/Коуровка Радиационное затухание колебаний корональных петель http://variable-stars.ru/db/msg/1176579/node4.html |
<< 2. Периода свободных колебаний | Оглавление | 4. Сила реакции излучения >>
3. Радиационное затухание колебаний петли во внешнем магнитном поле
Исследуем возбуждение МГД-волн слабоискривленной корональной петлей, колеблющейся во внешнем магнитном поле. Для этого рассчитаем поток волновой энергии, уносимой этими волнами с единицы поверхности цилиндра, совершающего во внешнем поле поперечные колебания заданной амплитуды.
Рассмотрим круглый прямой цилиндр длины L, радиуса поперечного сечения
а, заполненный однородным магнитным полем и идеально
проводящей плазмой. Магнитное поле В во внешней среде также
считаем соосным цилиндру и однородным, а плазму плотности 
-
идеально проводящей. Пусть цилиндр без изменения своей формы и размера
совершает в направлении оси х поперечные гармонические колебания
(рис. 2,а), т.е. его ось меняет положение со временем по закону
х = Х(t),
где:
- амплитуда, 
- частота
колебаний. Каждая точка поверхности цилиндра движется со скоростью
.
Будем для простоты расчетов считать колебания достаточно малыми:
, несмотря на то, что амплитуда реально
наблюдаемых колебаний петель (в среднем около 4 тысяч км)
превышает
, которое, по данным TRACE составляет, как отмечалось во Введении, 1-2
тысячи км, а по данным аппарата SOHO - 3-4 тысячи км (см. обсуждение в
[1]). В пользу принятого нами подхода имеются следующие аргументы:
во-первых, приближение малости поперечных колебаний может привести только
к недооценке изучаемого эффекта радиационного затухания. Если уже в этом
приближении удается решить проблему, то, очевидно, нет необходимости
строить значительно более сложную теорию нелинейных колебаний.
Во-вторых, необходимо учесть, что наблюдениями фиксируется только
центральная, наиболее плотная и горячая часть корональной магнитной петли.
Радиус ее эффективного сечения
, используемый в
МГД-моделях, заведомо превышает
.
(В работе [1] на стр. 890 для численных
оценок принималось
= 3600 км).
 |
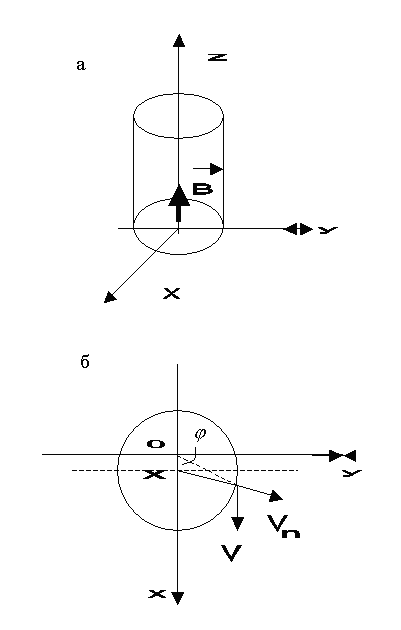Рис. 2. а). Цилиндр, совершающий поперечные колебания вдоль оси Х. б). Вид сверху. Приближение малых колебаний |
Таким образом, в реальной ситуации, видимо,
, но мы выбираем приближение малых колебаний, как
вполне достаточное для описания основного эффекта.
В указанном приближении для нормальной к поверхности цилиндра составляющей скорости можно принять (рис. 2,б):
Рассмотрим волны, возбуждаемые цилиндром во внешней среде. Линеаризованные уравнения идеальной МГД для однородной плазмы имеют вид:
Здесь 
, 
, 
,
- невозмущенные
параметры среды, 
, , 
, 
- возмущения. Будем
рассматривать решение вида:
В этом случае система (6)-(8) дает:
Отсюда следует:
где использовано обычное обозначение:
.
Общее решение уравнения (16) можно записать через функции Ганкеля следующим образом:
, С
, D
- произвольные константы. Можно показать, что первая из функций Ганкеля
описывает волны, расходящиеся от цилиндра,
а вторая
- волны, сходящиеся к оси
симметрии из бесконечности, что физически бессмысленно, поэтому сразу
исключим 
из рассмотрения, положив в (17) А = 0. Рассмотрим
первую цилиндрическую моду решения (17), приняв m = 1, D = 0. Тогда:
Константу С найдем из граничного условия непрерывности нормальной составляющей скорости на поверхности цилиндра: при
,
или,
используя (14):
Отсюда получаем:
. Следовательно, внешнее
решение краевой задачи имеет вид:
(Для полноты исследования можно было бы записать и внутреннее решение, определив его константы через условия непрерывности нормальной скорости и полного давления на границе. Но, как уже отмечалось, для решения данной задачи для нас основной интерес представляет именно внешнее решение, определяющее эффект радиационного затухания).
Поток волновой энергии определяется вектором Умова-Пойтинга:
то
Далее, учитывая, что
получаем:
Используя последнюю формулу и выделяя в решении (21) , (22) реальные части, можно рассчитать усредненный по периоду колебаний поток волновой энергии, уносимой с поверхности цилиндра произвольного радиуса r и длины L в единицу времени. Опуская громоздкие промежуточные выкладки, запишем окончательный результат:
Вычислив определитель Вронского для уравнения Бесселя, можно показать, что
Отсюда видно, что поток энергии р не зависит от расстояния 
от
оси цилиндра и определяется квадратом амплитуды колебаний.
Учитывая асимптотику функций Бесселя первого и второго рода:
выражение для потока волновой энергии удобно представить в форме:
Подчеркнем, что в это выражение входят только доступные для измерений величины: геометрические размеры петли, напряженность магнитного поля, частота и амплитуда колебаний.
В первом разделе было получено выражение для энергии возмущения магнитной
петли:
,
соответствующей среднему по петле отклонению
в некоторый момент
времени. Разделив его на поток энергии р и период колебаний
Т, мы
получим число, показывающее за какое количество периодов энергия системы,
запасенная при первоначальном возмущении, будет рассеяна в результате
излучения волн в окружающее пространство. Умножая это число на 2
,
найдем добротность колебательной системы, т.е. выразим ту же величину в
радианах:
Отметим, что поскольку р и 
зависят одинаковым
(квадратичным) образом от амплитуды смещения
,
то в (29) эта величина
сокращается. Аргумент Бесселевых функций в (29)
в данном случае достаточно
мал: 
. Ниже для численных оценок мы будем принимать
следующие величины:
см/с (согласно оценке,
приведенной в [1]);
cм
(в согласии с [1] и в
соответствии с изложенными выше соображениями, о том, что реальный радиус
магнитной трубки заведомо превышает его наблюдаемую величину); для частоты
колебаний и длины трубки примем данные для петли, рассмотренной в [4]: L =
130 000 км, частота
Гц, что соответствует
периоду колебаний Т = 256,4 с. В этом случае получается:
.
Учитывая рекуррентные соотношения
.
Следовательно:
Подстановка в эту формулу приведенных выше численных величин дает Q 
8.756.
<< 2. Периода свободных колебаний | Оглавление | 4. Сила реакции излучения >>