Astronet Астронет:  Научная Сеть/НС Колебания и волны
http://variable-stars.ru/db/msg/1175791/page34.html

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

Волны глубокой воды.

Если $kH \gg 1\; (H \gg \lambda ),$ то такие волны называют волнами глубокой воды. Возмущения $\delta p$ сосредоточены в приповерхностном слое толщиной $\sim \lambda$ и не "чувствуют" присутствия дна. Для таких волн, с учетом приближения ${\displaystyle \rm th}\; (kH) \approx 1,$ дисперсионное соотношение (6.19) примет вид:

$ \omega = \sqrt {\displaystyle gk}. $(6.21)

Таким образом, эти волны обладают сильной дисперсией.

Сделаем некоторые оценки. В океане преобладают волны с периодом колебаний $T\sim 10 с.$ Согласно (6.21) длина волны $\lambda = 2\pi / k\sim 150 м,$ а фазовая скорость $c\sim 15 м/с.$ Такая скорость является типичной, так как она совпадает с характерной скоростью ветра вблизи поверхности, генерирующего волны глубокой воды.

Если проанализировать распределение возмущений давления с глубиной, описываемое функцией $f(z)$ (см. (6.16)), то можно показать, что $f = e^{ - 1}$ при $z = \lambda / 6 = 25 м.$ Таким образом, приближение глубокой воды справедливо в тех местах, где глубина $H \geq 25 м.$

Волны мелкой воды.

При приближении к берегу глубина $H$ уменьшается, и реализуется условие $kH \lt 1\; (2\pi H \lt \lambda ).$ Хотя частота волны остается прежней, однако дисперсионное соотношение примет иной вид:

$ \omega = k\sqrt {\displaystyle gH} = kc_{0}, $(6.22)

из которого следует, что на мелкой воде дисперсия волн отсутствует. Скорость волн $c_{0} = \sqrt {\displaystyle gH}$ уменьшается с глубиной, и на глубине $H = 1 м$ скорость $c_{0} \sim 3 м/с,$ а длина волны при $T\sim 10 с$ равна $\lambda = c_{0} T\sim 30 м.$

В непосредственной близости к берегу, где глубина $H$ сравнима с амплитудой волны $s_{0},$ волна искажается - появляются крутые гребни, которые движутся быстрее самой волны и затем опрокидываются. Это происходит потому, что глубина под гребнем равна $H + s_{0}$ и превосходит глубину под впадиной $H - s_{0}.$ В результате колебания частиц волны приобретают сложный характер. По аналогии со звуками музыкальных инструментов, осциллограммы которых показаны в предыдущей лекции, можно сказать, что колебания частиц воды являются суперпозицией колебаний многих частот, причем по мере приближения к берегу ширина частотного спектра увеличивается. С подобным искажением акустических волн мы встретимся несколько позднее, когда будем изучать нелинейное распространение волн конечной амплитуды.

Из приведенной выше классификации гравитационных волн следует, что для океана с глубиной $H = 5 км$ волны глубокой воды должны иметь $\lambda \lt 2\pi H\sim 30 км.$ Согласно (6.21) их период колебаний $T = 2\pi / \omega \leq 2 мин.$, а скорость $c = \lambda / T \leq 250 м/с$. Для континентального шельфа $H\sim 50 м,$ поэтому волнами глубокой воды будут волны с $\lambda \leq 300 м,\; T \leq 15 с$ и $c \leq 20 м/с.$

С другой стороны, на глубине H \sim 5 км волны с длинами волн $\lambda \geq 30 км$ будут волнами мелкой воды. Эти волны имеют период колебаний $T \geq 2 мин.$, а их скорость $c \geq 250 м/с$. Такие волны двигаются со скоростью реактивного самолета и могут пересечь Атлантический океан примерно за 7 часов.

Характер движения частиц жидкости.

Рассчитаем скорости частиц $v_{x}$ и $v_{z},$ как функции координат $x, z$ и времени $t.$ Это легко сделать из уравнений (6.6) с учетом (6.3), (6.1) и (6.16):

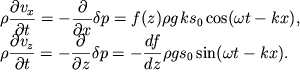$ \begin{array}{l} \rho {\displaystyle \frac{\displaystyle {\displaystyle \partial v_{x} }}{\displaystyle {\displaystyle \partial t}}} = - {\displaystyle \frac{\displaystyle {\displaystyle \partial }}{\displaystyle {\displaystyle \partial x}}}\delta p = f(z)\rho g{\displaystyle \kern 1pt} ks_{0} \cos (\omega t - kx), \\ \rho {\displaystyle \frac{\displaystyle {\displaystyle \partial v_{z} }}{\displaystyle {\displaystyle \partial t}}} = - {\displaystyle \frac{\displaystyle {\displaystyle \partial }}{\displaystyle {\displaystyle \partial z}}}\delta p = - {\displaystyle \frac{\displaystyle {\displaystyle df}}{\displaystyle {\displaystyle dz}}}\rho gs_{0} \sin (\omega t - kx). \\ \end{array} $(6.23)

Отсюда

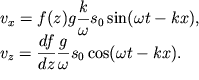$ \begin{array}{l} v_{x} = f(z)g{\displaystyle \frac{\displaystyle {\displaystyle k}}{\displaystyle {\displaystyle \omega }}}s_{0} \sin (\omega t - kx), \\ v_{z} = {\displaystyle \frac{\displaystyle {\displaystyle df}}{\displaystyle {\displaystyle dz}}}{\displaystyle \frac{\displaystyle {\displaystyle g}}{\displaystyle {\displaystyle \omega }}}s_{0} \cos (\omega t - kx). \\ \end{array} $(6.24)

На рис. 6.5 показаны векторы скорости частиц на глубине $z$ и на поверхности в фиксированный момент времени. Пунктиром изображено положение волны через малый промежуток времени. Под гребнем волны частицы имеют составляющую скорости $v_{x} \gt 0,$ а под впадиной $v_{x} \lt 0.$ Скорость некоторой частицы A направлена вниз, и с течением времени будет изменяться. Легко понять, что в последующий момент скорость частицы A будет такой, как у частицы B в настоящий момент, затем - как у частицы C в настоящий момент, и так далее. Поэтому траектория частицы A будет эллиптической. По мере увеличения координаты $z$ (глубины погружения) $v_{z} \to 0,$ эллипсы сплющиваются, и при $z \geq \lambda$ частицы жидкости колеблются практически вдоль оси Ox.

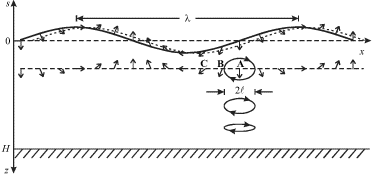Рис. 6.5.

Размер $\ell$ большой полуоси эллипса можно оценить из условия

$ \ell \approx (v_{x} )_{max} T = g{\displaystyle \frac{\displaystyle {\displaystyle k}}{\displaystyle {\displaystyle \omega }}}s_{0} T. $(6.25)

Сравним $\ell$ с длиной волны $\lambda$ :

$ {\displaystyle \frac{\displaystyle {\displaystyle \ell }}{\displaystyle {\displaystyle \lambda }}} \approx {\displaystyle \frac{\displaystyle {\displaystyle g}}{\displaystyle {\displaystyle \lambda }}}{\displaystyle \frac{\displaystyle {\displaystyle k}}{\displaystyle {\displaystyle \omega }}}s_{0} T. $(6.26)

Учтем, что $\omega / k = c,\; \lambda = cT,\; c_{0} = \sqrt {\displaystyle gH}$ - скорость волн мелкой воды. Тогда

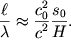$ {\displaystyle \frac{\displaystyle {\displaystyle \ell }}{\displaystyle {\displaystyle \lambda }}} \approx {\displaystyle \frac{\displaystyle {\displaystyle c_{0}^{2} }}{\displaystyle {\displaystyle c^{2}}}}{\displaystyle \frac{\displaystyle {\displaystyle s_{0} }}{\displaystyle {\displaystyle H}}}. $(6.27)

Для мелкой воды $c = c_{0},$ и

$ {\displaystyle \frac{\displaystyle {\displaystyle \ell }}{\displaystyle {\displaystyle \lambda }}} = {\displaystyle \frac{\displaystyle {\displaystyle s_{0} }}{\displaystyle {\displaystyle H}}} \ll 1. $(6.28)

Поскольку в этом случае $\lambda \sim H,$ то $\ell \sim s_{0},$ т.е. возрастает с ростом амплитуды волны $s_{0}.$ Но так как $s_{0} \ll H,$ то амплитуда горизонтальных колебаний $\ell \ll \lambda.$

Частицы на поверхности глубокой жидкости движутся по траекториям, близким к круговым. По таким же траекториям будет двигаться и плавающее на поверхности небольшое тело, например, притопленный поплавок.

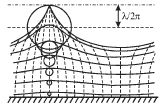
До сих пор мы предполагали, что профиль волны является синусоидальным, что возможно только в том случае, если амплитуда волны очень мала по сравнению с ее длиной. В природе таким профилем реально обладают только приливные волны, длина которых чрезвычайно велика по сравнению с их высотой. Обычные ветровые волны имеют более сложный вид. Как показывают расчеты, частицы жидкости в них движутся по окружностям, радиус которых экспоненциально убывает с глубиной (см. рис. 6.6). Сплошными линиями на рисунке показаны линии равного давления, любая из которых может соответствовать поверхности воды при определенной амплитуде волны. Эти линии являются трохоидами - траекториями точек, расположенных на радиусе между центром и ободом колеса, катящегося под горизонтальной прямой, расположенной на высоте ${\displaystyle \frac{\displaystyle {\displaystyle \lambda }}{\displaystyle {\displaystyle 2\pi }}}$ над уровнем невозмущенной поверхности воды. Поэтому такая волна называется трохоидальной и отличается от синусоидальной гармонической волны, задаваемой формулой (6.1). Очень близкими к трохоидальным являются волны после наступления на море штиля. Это так называемая мертвая зыбь. В частном случае, когда радиус орбиты частицы, находящейся на поверхности воды, равен ${\displaystyle \frac{\displaystyle {\displaystyle \lambda }}{\displaystyle {\displaystyle 2\pi }}},$ профиль волны имеет вид циклоиды (верхняя кривая на рис. 6.6). Однако, опыт показывает, что циклоидальная форма поверхности воды может наблюдаться только у стоячих волн.

Рис. 6.6.

Опытным путем также установлено, что у бегущих трохоидальных волн угол между касательной к поверхности воды и горизонтом не превышает $\sim 30^\circ.$ Если угол ската у гребня волны превышает это значение, которое соответствует отношению амплитуды трохоидальной волны к ее длине ${\displaystyle \frac{\displaystyle {\displaystyle s_{0} }}{\displaystyle {\displaystyle \lambda }}} \approx {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 4\pi }}} \approx 0,08,$ то волна теряет устойчивость. Это явление играет большую роль в процессе зарождения и развития волн, что можно заметить, наблюдая за ними в присутствии ветра. Высокие волны с острыми гребешками не могут продолжать свой бег, так как их гребни опрокидываются и разрушаются, и волны уменьшаются по высоте.

Назад| Вперед

Rambler's Top100 Яндекс цитирования