Астронет > Механика твердого тела. Лекции.

Астронет: Физический факультет МГУ Механика твердого тела. Лекции.
http://variable-stars.ru/db/msg/1175788/page14.html

Механика твердого тела. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 1997 г. Содержание

Лекция 4.

Гироскопы. Свободный гироскоп. Прецессия гироскопа под действием внешних сил. Угловая скорость прецессии. Нутации. Гироскопические силы, их природа и проявления.

Волчки. Устойчивость вращения симметричного волчка.

Гироскоп - это массивное аксиально-симметричное тело, вращающееся с большой угловой скоростью вокруг своей оси симметрии.

В этом случае моменты всех внешних сил, включая и силу тяжести, относительно центра масс гироскопа равны нулю. Это можно реализовать, например, поместив гироскоп в карданов подвес, описанный в лекции 3 и изображенный на рис. 3.13.

При этом

${\displaystyle \bf M}= 0;\quad {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf L}}}{\displaystyle {\displaystyle dt}}} = 0,$

(4.1)

и момент импульса сохраняется:

${\displaystyle \bf L} = {\displaystyle \rm const}.$

(4.2)

Гироскоп ведет себя так же, как и свободнее тело вращения (см. лекцию 3). В зависимости от начальных условий возможны два варианта поведения гироскопа:

1. Если гироскоп раскручен вокруг оси симметрии, то направления момента импульса и угловой скорости совпадают:

${\displaystyle \bf L} = J\omega = {\displaystyle \rm const},$

(4.3)

и направление оси симметрии гироскопа остается неизменным. В этом можно убедиться, поворачивая подставку, на которой расположен карданов подвес - при произвольных поворотах подставки ось гироскопа сохраняет неизменное направление в пространстве. По этой же причине волчок, "запущенный" на листе картона и подброшенный вверх (рис. 4.1), сохраняет направление своей оси во время полета, и, падая острием на картон, продолжает устойчиво вращаться, пока не израсходуется запас его кинетической энергии.

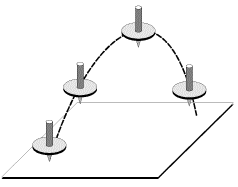Рис. 4.1.

Свободный гироскоп, раскрученный вокруг оси симметрии, обладает весьма значительной устойчивостью. Из основного уравнения моментов следует, что изменение момента импульса

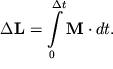$\Delta {\displaystyle \bf L} = {\displaystyle \int\limits_{0}^{\Delta t} {\displaystyle {\displaystyle \bf M}} } \cdot dt.$

(4.)

Если интервал времени $\Delta t$ мал, то и $\Delta {\displaystyle \bf L}$ мало, то есть при кратковременных воздействиях даже очень больших сил движение гироскопа изменяется незначительно. Гироскоп как бы сопротивляется попыткам изменить его момент импульса и кажется "затвердевшим".

Возьмем гироскоп конусообразной формы, опирающийся на стержень подставки в своем центре масс О (рис. 4.2). Если тело гироскопа не вращается, то оно находится в состоянии безразличного равновесия, и малейший толчок сдвигает его с места.. Если же это тело привести в быстрое вращение вокруг своей оси, то даже сильные удары деревянным молотком не смогут сколько-нибудь значительно изменить направление оси гироскопа в пространстве. Устойчивость свободного гироскопа используется в различных технических устройствах, например, в автопилоте.

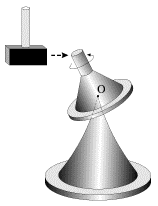Рис. 4.2.

2. Если свободный гироскоп раскручен так, что вектор мгновенной угловой скорости и ось симметрии гироскопа не совпадают (как правило, это несовпадение при быстром вращении бывает незначительным), то наблюдается движение, описанное в лекции 3 как "свободная регулярная прецессия". Применительно же к гироскопу его называют нутацией. При этом ось симметрии гироскопа, векторы L и $\omega$ лежат в одной плоскости, которая вращается вокруг направления $\bf L}= {\displaystyle \rm const$ с угловой скоростью, равной ${\displaystyle \frac{\displaystyle {\displaystyle L}}{\displaystyle {\displaystyle J_{x} }}},$ где $J_{x}$ - момент инерции гироскопа относительно главной центральной оси, перпендикулярной оси симметрии. Эта угловая скорость (назовем ее скоростью нутации) при быстром собственном вращении гироскопа оказывается достаточно большой, и нутация воспринимается глазом как мелкое дрожание оси симметрии гироскопа.

Нутационное движение легко продемонстрировать с помощью гироскопа, показанного на рис. 4.2 - оно возникает при ударах молотком по стержню вращающегося вокруг своей оси гироскопа. При этом чем сильнее раскручен гироскоп, тем больше его момент импульса L - тем больше скорость нутации и тем "мельче" дрожания оси фигуры. Этот опыт демонстрирует еще одну характерную особенность нутации - с течением времени она постепенно уменьшается и исчезает. Это - следствие неизбежного трения в опоре гироскопа.

Наша Земля - своего рода гироскоп, и ей тоже свойственно нутационное движение. Это связано с тем, что Земля несколько приплюснута с полюсов, в силу чего моменты инерции относительно оси симметрии $\left( {\displaystyle J_{z} } \right)$ и относительно оси, лежащей в экваториальной плоскости $\left( {\displaystyle J_{x} , J_{y} } \right)$ различаются. При этом $J_{x} = J_{y} ,$ а ${\displaystyle \frac{\displaystyle {\displaystyle J_{z} - J_{x} }}{\displaystyle {\displaystyle J_{x} }}} \approx {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 300}}}.$ В системе отсчета, связанной с Землей, ось вращения движется по поверхности конуса вокруг оси симметрии Земли с угловой скоростью $\omega _{0} ,$ рассчитываемой по формуле (3.58), то есть она совершает один оборот примерно за 300 дней. На самом деле в силу, как предполагается, неабсолютной жесткости Земли, это время оказывается больше - оно составляет около 440 суток. При этом расстояние точки земной поверхности, через которую проходит ось вращении, от точки, через которую проходит ось симметрии (Северный полюс), равно всего нескольким метрам. Нутационное движение Земли не затухает - по-видимому, его поддерживают сезонные изменения, происходящие на поверхности

Прецессия гироскопа под действием внешних сил. Элементарная теория.

Рассмотрим теперь ситуацию, когда к оси гироскопа приложена сила, линия действия которой не проходит через точку закрепления. Опыты показывают, что в этом случае гироскоп ведет себя весьма необычным образом.

Если к оси шарнирно закрепленного в точке О гироскопа (рис. 4.3) прикрепить пружину и тянуть за нее вверх с силой F , то ось гироскопа будет перемещаться не в направлении силы, а перпендикулярно к ней, вбок. Это движение называется прецессией гироскопа под действием внешней силы.

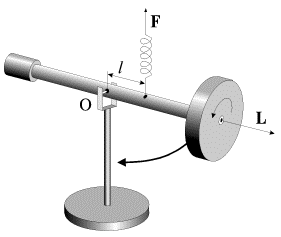Рис. 4.3.

Опытным путем можно установить, что угловая скорость прецессии зависит не только от величины силы $F$ (рис. 4.3), но и от того, к какой точке оси гироскопа эта сила приложена: с увеличением $F$ и ее плеча $\ell$ относительно точки закрепления О скорость прецессии увеличивается. При этом оказывается, что чем сильнее раскручен гироскоп, тем меньше угловая скорость прецессии при данных $F$ и $\ell .$

В качестве силы F, вызывающей прецессию, может выступать сила тяжести, если точка закрепления гироскопа не совпадает с центром масс. Так, если стержень с быстро вращающимся диском подвесить на нитке (рис. 4.4), то он не опускается вниз, как это можно было бы предположить, а совершает прецессионное движение вокруг нитки. Наблюдение прецессии гироскопа под действием силы тяжести в некотором смысле даже удобнее - линия действия силы "автоматически" смещается вместе с осью гироскопа, сохраняя свою ориентацию в пространстве.

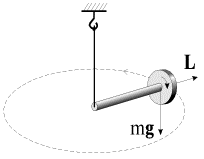Рис. 4.4.

Можно привести и другие примеры прецессии - например, движение оси хорошо известной детской игрушки - юлы с заостренным концом (рис. 4.5). Юла, раскрученная вокруг своей оси и поставленная на горизонтальную плоскость слегка наклонно, начинает прецессировать вокруг вертикальной оси под действием силы тяжести (рис. 4.5).

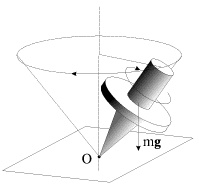Рис. 4.5.

Точное решение задачи о движении гироскопа в поле внешних сил довольно выражение для угловой скорости прецессии можно легко получить в рамках так называемой элементарной теории гироскопа. В этой теории делается допущение, что мгновенная угловая скорость вращения гироскопа и его момент импульса направлены вдоль оси симметрии гироскопа. Другими словами, предполагается, что угловая скорость вращения гироскопа вокруг своей оси значительно больше угловой скорости прецессии:

$\omega \gg \Omega ,$

(4.5)

так что вкладом в L, обусловленным прецессионным движением гироскопа, можно пренебречь. В этом приближении момент импульса гироскопа, очевидно, равен

${\displaystyle \bf L} = J_{z} \omega,$

(4.6)

где $J_{z}$ - момент инерции относительно оси симметрии.

Итак, рассмотрим тяжелый симметричный гироскоп, у которого неподвижная точка S (точка опоры о подставку) не совпадает с центром масс О (рис. 4.6).

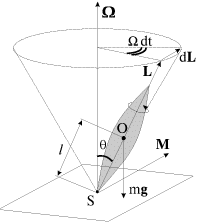Рис. 4.6.

Момент силы тяжести относительно точки S

$M = mg\ell \sin \theta ,$

(4.7)

где $\theta$ - угол между вертикалью и осью симметрии гироскопа. Вектор M направлен по нормали к плоскости, в которой лежат ось симметрии гироскопа и вертикаль, проведенная через точку S (рис. 4.6). Сила реакции опоры проходит через S , и ее момент относительно этой точки равен нулю.

Изменение момента импульса L определяется выражением

$d{\displaystyle \bf L} = {\displaystyle \bf M} \cdot dt.$

(4.8)

При этом и L, и ось волчка прецессируют вокруг вертикального направления с угловой скоростью $\Omega.$ Еще раз подчеркнем: делается допущение, что выполнено условие (4.5) и что L постоянно направлен вдоль оси симметрии гироскопа. Из рис. 4.6 следует, что

$dL = L \cdot \sin \theta \cdot \Omega \cdot dt.$

(4.9)

В векторном виде

$d{\displaystyle \bf L} = \Omega\times {\displaystyle \bf L} \cdot dt.$

(4.10)

Сравнивая (4.8) и (4.10), получаем следующую связь между моментом силы M, моментом импульса L и угловой скоростью прецессии $\Omega$ :

${\displaystyle \bf M} = \Omega\times {\displaystyle \bf L}.$

(4.11)

Это соотношение позволяет определить направление прецессии при заданном направлении вращения волчка вокруг своей оси.

Обратим внимание, что M определяет угловую скорость прецессии, а не угловое ускорение, поэтому мгновенное "выключение" M приводит к мгновенному же исчезновению прецессии, то есть прецессионное движение является безынерционным.

Сила, вызывающая прецессионное движение, может иметь любую природу. Для поддержания этого движения важно, чтобы вектор момента силы M поворачивался вместе с осью гироскопа. Как уже было отмечено, в случае силы тяжести это достигается автоматически. При этом из (4.11) (см. также рис. 4.6) можно получить:

$mg\ell \cdot \sin \theta = \Omega J_{z} \omega \sin \theta .$

(4.12)

Если учесть, что в нашем приближении справедливо соотношение (4.6), то для угловой скорости прецессии получим

$\Omega = {\displaystyle \frac{\displaystyle {\displaystyle mg\ell }}{\displaystyle {\displaystyle J_{z} \omega }}}.$

(4.13)

Следует отметить, что $\Omega$ не зависит от угла $\theta$ наклона оси гироскопа и обратно пропорциональна $\omega ,$ что хорошо согласуется с опытными данными.

Назад| Вперед