 |
Астронет: А. Н. Петров/ГАИШ Законы сохранения в ОТО и их приложения http://www.astronet.ru/db/msg/1170672/node9.html |
- 2.2.1 Обоснование использования метода Белинфанте в модели КБЛ
- 2.2.2 Приложение метода Белинфанте к КБЛ модели
- 2.2.3 Свойства новых законов сохранения
2.2 Приложение процедуры Белинфанте к модели Каца, Бичака и Линден-Белла
2.2.1 Обоснование использования метода Белинфанте в модели КБЛ
Необходимость использования фона заложена в самом определении метода Белинфанте [1]. В теориях с лагранжианом (2.9) взаимодействия расссматриваются на заданном фоне, который является необходимой составляющей модели, и это приводит к успеху применения метода. Симметризуя псевдотензор Эйнштейна, Папапетроу [3] вынужден был использовать вспомогательную метрику Минковского. И, действительно, применение этого метода в ОТО без использования фона [4] дает ,,неразумные'' нулевые результаты для сохраняющихся величин. Можно ли в ОТО, в более сложных случаях, чем рассмотрел Папапетроу [3], применять этот метод?
Cнова вспомним о модели
Каца-Бичака-Линден-Белла [5] (КБЛ), которая была подробно изложена
в лекции 1. С одной стороны, в модель КБЛ
включена фоновая метрика, напомним, КБЛ лагранжиан есть
![]()
![]() ,
,
![]() .
.
форма тока стандартна:
с обобщенным тензором энергии-импульса
- 1. Один из них состоит в том, что невозможно построить
угловой момент изолированной системы только с помощью
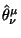 , необходимо привлечь тензор спина
, необходимо привлечь тензор спина
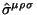 . Представляется более предпочтительным,
если одни и те же свойства модели описываются минимальным количеством
объектов, а лучше единым. Именно для этого предназначен
Белинфанте метод. Именно поэтому многие авторы 50-х годов,
включая Ландау и Лифшица [6], Голдберга [7],
стремились построить симметричные псевдотензоры.
Стараясь избежать использования спинового члена, Папапетроу [3]
применил метод Белинфанте к псевдотензору Эйнштейна.
. Представляется более предпочтительным,
если одни и те же свойства модели описываются минимальным количеством
объектов, а лучше единым. Именно для этого предназначен
Белинфанте метод. Именно поэтому многие авторы 50-х годов,
включая Ландау и Лифшица [6], Голдберга [7],
стремились построить симметричные псевдотензоры.
Стараясь избежать использования спинового члена, Папапетроу [3]
применил метод Белинфанте к псевдотензору Эйнштейна.
- 2. Другой вопрос состоит в том, что форма канонических величин,
определяемых методом Нетер, зависит от дивергенций, которые могут быть
добавлены к лагранжиану. А это означает, что для разных граничных
условий мы должны использовать каждый раз совсем различные величины. С
одной стороны, в этом нет трагедии. В термодинамике так и происходит, и
авторы работ [8]
 [9], аппелируя к такой аналогии находят в этом
преимущество. С другой стороны, например, выражение для плотности энергии
вибрирующей струны не зависит от того, как закреплены ее концы,
оно всегда одно и то же. Исходя из этого мы хотели бы изменить
так КБЛ модель, чтобы общая форма сохраняющегося тока и суперпотенциала
не зависели от дивергенций в лагранжиане.
[9], аппелируя к такой аналогии находят в этом
преимущество. С другой стороны, например, выражение для плотности энергии
вибрирующей струны не зависит от того, как закреплены ее концы,
оно всегда одно и то же. Исходя из этого мы хотели бы изменить
так КБЛ модель, чтобы общая форма сохраняющегося тока и суперпотенциала
не зависели от дивергенций в лагранжиане.
2.2.2 Приложение метода Белинфанте к КБЛ модели
В остатке этой части лекции 2 излагаются результаты,
опубликованные в работах [10]![]() [12]. Итак, для спиновых
коэффициентов КБЛ построим поправку Белинфанте по стандартным
правилам (2.17):
[12]. Итак, для спиновых
коэффициентов КБЛ построим поправку Белинфанте по стандартным
правилам (2.17):
где введем обозначения для новых тока и суперпотенциала, и представим структуру тока:
Заметим, что спиновый член, как и положено, отсутствует. ,,Симметризованный'' обобщенный тензор энергии-импульса имеет вид:
а Z-член, как и везде, обращается в нуль на киллинговых векторах фона.
Новый суперпотенциал имеет форму:
интересна и сама по себе: для
2.2.3 Свойства новых законов сохранения
В результате сохранены все полезные свойства КБЛ модели, коротко повторим их:
- (i) Построен сохраняющийся ток:
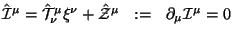 .
.
- (ii)
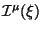 определяется Нетер-Белинфанте
процедурой и данным лагранжианом.
См. обсуждение вопроса единственности в следующей части лекции 2.
определяется Нетер-Белинфанте
процедурой и данным лагранжианом.
См. обсуждение вопроса единственности в следующей части лекции 2.
- (iii) Сохранена общая ковариантность.
- (iv) Законы сохранения работают на произвольно
искривленных фонах.
- (v) Используются произвольные
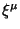 .
.
- (vi) Построен соответствующий антисимметричный суперпотенциал.
- (vii) Удовлетворяются необходимые естественные тесты.
Кроме сохраненных свойств появились новые:
 (viii) Спиновый член исчез из
определения тока. Для любого фонового вектора Киллинга
(в том числе для пространственных вращений, если они присутствуют)
будет использоваться сохраняющийся ток, определяемый ТОЛЬКО
обобщенным тензором энергии-импульса:
(viii) Спиновый член исчез из
определения тока. Для любого фонового вектора Киллинга
(в том числе для пространственных вращений, если они присутствуют)
будет использоваться сохраняющийся ток, определяемый ТОЛЬКО
обобщенным тензором энергии-импульса:
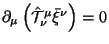 .
См. также обсуждение далее.
.
См. также обсуждение далее.
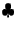 (ix) Величины
(ix) Величины
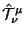 ,
,
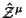 и
и
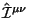 не зависят от дивергенций в лагранжиане.
См. обсуждение в следующей части лекции 2.
не зависят от дивергенций в лагранжиане.
См. обсуждение в следующей части лекции 2.
 (x) Свойства нового обобщенного тензора
энергии-импульса.
(x) Свойства нового обобщенного тензора
энергии-импульса.
Tензор энергии-импульса в (2.24) имеет вид:
(a) Как и в каноническом аналоге, первое слагаемое -- это возмущение материального тензора энергии-импульса, правда теперь симметризованное.
(b) Второй член -- это симметричный тензор энергии-импульса свободного гравитационного поля:
(c) Последние два члена в (2.28) отвечают за ,,потенциальное'' взаимодействие с фоновой геометрией. Первый из них симметричен, второй -- антисимметричен. Это приводит к тому, что
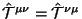 если и только если
если и только если
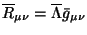 с постоянной
с постоянной
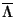 ,
то есть если фоновое пространство-время -- это пространство Эйнштейна
по Петрову [13]. Таким образом, симметризация Белинфанте при обобщении
на искривленные фоны оказалась ограниченной -- в смысле ,,симметризации'' --
пространствами Эйнштейна.
,
то есть если фоновое пространство-время -- это пространство Эйнштейна
по Петрову [13]. Таким образом, симметризация Белинфанте при обобщении
на искривленные фоны оказалась ограниченной -- в смысле ,,симметризации'' --
пространствами Эйнштейна.
(d) В лекции 1 мы определились, что для построения глобальных законов сохранения важным является ,,дифференциальное'' сохранение тока. Тем не менее, интересно: выполняется ли дифференциальный закон сохранения для обобщенного тензора энергии-импульса? Оказывается, что
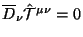 если и только если
если и только если
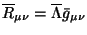 ,
для более сложных
,
для более сложных
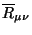 получим
получим
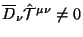 .
.
(e) Несмотря на то, что в случае самого общего фона нет симметризации тензора энергии-импульса и нет дифференциального закона сохранения для тензора энергии-импульса, метод Белинфанте выпонил свою задачу. Ток сохраняется на всех произвольно искривленных фонах без явного участия спинового члена. В случае если
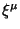 равен
равен 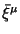 -- вектору Киллинга фона,
то этот закон сохранения упрощается до:
-- вектору Киллинга фона,
то этот закон сохранения упрощается до:
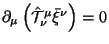 ,
где участвует только
,
где участвует только
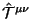 ,
хотя бы и не симметричный(!),
хотя бы и
,
хотя бы и не симметричный(!),
хотя бы и
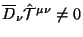 (!).
Это представляется важным для приложений в космологических задачах.
Действительно, решения Фридмана не являются пространствами
Эйнштейна, но они обладают, например, киллинговыми векторами
вращений
(!).
Это представляется важным для приложений в космологических задачах.
Действительно, решения Фридмана не являются пространствами
Эйнштейна, но они обладают, например, киллинговыми векторами
вращений
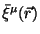 . Это значит, что с помощью
. Это значит, что с помощью
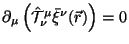 ,
могут быть расчитаны угловые моменты астрофизических объектов на
фоне фридмановской геометрии.
,
могут быть расчитаны угловые моменты астрофизических объектов на
фоне фридмановской геометрии.
(f) Остался вопрос о вторых производных в тензоре энергии-импульса (2.29). Вообще говоря, в теории с уравнениями второго порядка их присутствие в тензоре энергии-импульса нежелательно в смысле постановки начальной задачи. Многие авторы (см., например, недавнюю работу [14]), предпочитают иметь только первые производные в тензоре энергии-им- пульса. Но давайте обсудим, так ли плохи наши дела. Пусть начальная гиперповерхность задается как x0=0. Глобальные величины, как мы их определили в лекции 1, задаются нулевой компонентой тока:
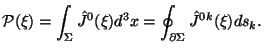
Нулевая компонента нового тока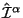 выражается через ток КБЛ и поправку Белинфанте
как
выражается через ток КБЛ и поправку Белинфанте
как
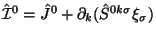 ;
(k=1, 2, 3). Осталась только пространственная дивергенция
по причине, что поправка
;
(k=1, 2, 3). Осталась только пространственная дивергенция
по причине, что поправка
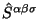 атисимметрична по первым двум индексам.
Но поскольку КБЛ ток
атисимметрична по первым двум индексам.
Но поскольку КБЛ ток 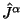 и поправка
и поправка
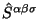 зависят только от первых производных, то
зависят только от первых производных, то
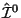 содержит только первые временные
производные.
Таким образом, начальная задача может быть определена
корректно.
содержит только первые временные
производные.
Таким образом, начальная задача может быть определена
корректно.
 (xi) Наконец, обсудим свойства нового суперпотенциала
(2.26).
(xi) Наконец, обсудим свойства нового суперпотенциала
(2.26).
(a) Как мы уже отметили, (2.26) антисимметричен в силу антисимметрии величины
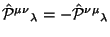 , определенной в (2.27).
Мы также отметили, что суперпотенциал (2.26)
обобщает
суперпотенциал
Папапетроу [3].
, определенной в (2.27).
Мы также отметили, что суперпотенциал (2.26)
обобщает
суперпотенциал
Папапетроу [3].
(b) На наш взгляд кажется важным, что новый суперпотенцил линейно зависит от возмущений метрической плотности:
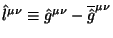 . Действительно, модель построена без приближений,
и в задачах, где рассмативаются возмущения относительно заданного фона
мы могли бы не заботиться о проблеме сходимости аппроксимаций в каждом
следующем порядке в зависимости от малости
. Действительно, модель построена без приближений,
и в задачах, где рассмативаются возмущения относительно заданного фона
мы могли бы не заботиться о проблеме сходимости аппроксимаций в каждом
следующем порядке в зависимости от малости
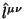 ,
так как наше выражение для суперпотенциала точное.
,
так как наше выражение для суперпотенциала точное.
(c) Существует другая полезная форма нового суперпотенциала:
![$\displaystyle \hat {\cal I}^{\mu\nu}=
{1 \over \kappa} \left(\hat l^{\rho[\mu}\...
...igma \hat
l^{\nu]\sigma}-\bar D^{[\mu}\hat l^{\nu ]}_\sigma \xi^\sigma \right).$](http://images.astronet.ru/pubd/2001/09/12/0001170672/img250.gif)
По форме этот суперпотенциал совпадает с суперпотенциалом Абботта-Дезера [15], однако они расходятся начиная со второго порядка возмущений, и это важно. Как было отмечено, наш новый суперпотенциал (2.26) удовлетворяет всем признанным естественным тестам, в то время как суперпотенциал Абботта-Дезера не дает правильного 4-импульса Бонди-Сакса для излучающей системы [12].
<< 2.1 Классический метод Белинфанте | Оглавление | 2.3 Обобщенная процедура Белинфанте ... >>