Астронет > Footnotes

Астронет: А. Г. Морозов, А. В. Хоперсков Физика Дисков
http://variable-stars.ru/db/msg/1168623/footnode.html

Физика Дисков

... процессов ¹ Система, состоящая из большого числа взаимодействующих частиц, обладает коллективными свойствами, что проявляется в самосогласованном движении всех частиц, имеющем волновой характер. Волны могут обмениваться энергией и импульсом. Такого рода взаимодействия называют коллективными. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
...22] ^1.1 Недостаток вещества в центральных областях звездных дисков по сравнению с законом (1.1.2) ("дыра" или депрессия плотности) заложен, например, в моделях Галактики [23,24] и ряде других [22]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... диска ^1.2 Здесь мы говорим о средней по всем типам звезд величине 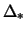. Относительно характера распределения звезд разных спектральных классов поперек плоскости диска см. в работе Бартая [26]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... бара ^1.3 Бар -- вытянутое овалоподобное образование в центре некоторых (SB) галактик ( см. разд. 1.3). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... классов ^1.4 Согласно работе [54], дисперсия скоростей звезд практически не зависит от их массы, но изменяется с их возрастом. Так, для звезд моложе 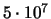лет величина 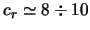км/с практически не отличается от дисперсии скоростей газовых облаков, а для звезд - карликов, возраст которых близок к возрасту Галактики ( 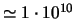лет), 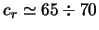км/с. 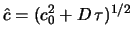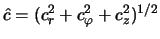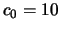Зависимость дисперсии скоростей звезд от их возраста удовлетворительно аппроксимируется выражением , где ; км/с; 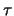-- возраст звезды (в годах); 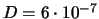(км/с)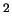/год. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... диска ^1.5 На периферии плоских галактик за пределами их спирального узора слой газа часто искривляется, отклоняясь от плоскости симметрии звездного диска на расстояние до нескольких килопарсек. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... диска ^1.6 За исключением далеких периферийных областей. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... галактику ^1.7 Такой спиральный узор называют grand design. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... узора ^1.8 Их также называют флукулентными спиралями (flocculent). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... фона ^1.9 В некоторых редко встречающихся галактиках ранних типов с крайне низким содержанием газа видны только слабоконтрастные спиральные ветви по старым звездам [97]. В галактиках с баром может наблюдаться весьма мощная (до 50%) волна плотности в старом населении диска [91]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... галактик ^1.10 В основном у эллиптических галактик, но есть и у нескольких спиральных типа Sa. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
...)^1.11 В среднем у Sa-галактик 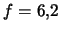, у Sb -- 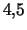, у Sc -- . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
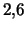... системах ^1.12 Первым на это обратил внимание Я.Б.Зельдович [130]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... систем ^1.13 При употреблении термина "тесная двойная система" обычно подразумевается наличие обмена масс между компонентами. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... недель ^1.14 В книге [118] приведен пример с RT Ser, у которой уменьшение на 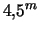произошло за 27 лет. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... II ^1.15 Впрочем, пока известен только один "Быстрый барстер" MXB 1730--335 с характерным временем повторения 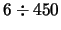с. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... изменится ^2.1 Относительно построения кинетического уравнения в произвольной ортогональной системе координат см. в монографии Поляченко и Фридмана [1]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... газа ^2.2 О роли газа см. гл. 4 и 6. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
...эпициклическим ^2.3 Подробнее см. пп. 1.1.3, 2.2.2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
...eq2.1.34)^2.4 Анализ влияния возможного отклонения функции распределения звезд по остаточным скоростям от анизотропного максвелловского на гравитационную устойчивость звездного диска проведен в п. 2.3.4. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... маргинальной ^2.5 Т.е. находящейся на границе устойчивости. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... виде ^2.6 В ряде работ в рамках различных моделей гравитирующего диска было показано, что ВКБ-приближение дает результаты, весьма близкие к точным и для крупномасштабных мод. Так, например, по Калнайсу [194], ВКБ-решение уравнения Пуассона для моды 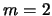, 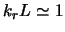отличается от точного не более, чем на 2%, а в работе [195] точные значения частот колебаний диска практически совпадают с вычисленными в коротковолновом приближении вплоть до самых крупномасштабных мод включительно. Поэтому использование ВКБ-приближения вполне может приводить к результатам удовлетворительной точности вплоть до 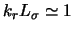. Это, однако, заведомо не относится к окрестностям динамических резонансов таких мод, где 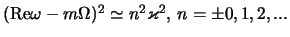-- см. ниже (2.2.22). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... соотношением ^2.7 Примесь "ям большей глубины", соответствующих четным по 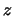-координате собственным функциям 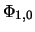, согласно [192] уменьшает величину в области 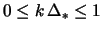не более, чем на 2%. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... ветви ^2.8 Термин "градиентная" обусловлен тем, что в однородном по 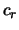и диске эта ветвь колебаний вырождается ( ). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
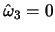... холодный ^2.9 "Температура" звездной системы характеризуется квадратами дисперсий скоростей звезд (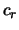, ,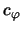), а газа -- скорости звука . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .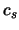
... слой ^2.10 Стpого говоpя в этом случае система нестационаpна. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
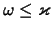... ^2.11 В бесстолкновительном диске имеются и высокочастотные колебания с 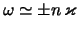, 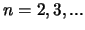[см.(2.2.38)]. По крайней мере в однородном диске они не влияют на гравитационную устойчивость. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
...^2.12 Аналогичный результат получен в работе [208]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... существенной ^2.13 К сожалению, эти трудности носят принципиальный характер. Выходом из этого положения может служить сравнение с контрольными численными экспериментами (см. гл. 3), в которых неоднородные системы выходят на границу устойчивости, и при необходимости корректировка критериев устойчивости такого типа. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... шланговая ^2.14 Термин, обычно употребляемый в физике плазмы и гидродинамике. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... значений ^3.1 В моделях PP при "измерении" макроскопических (в том числе и локальных) параметров диска, приходящего в состояние, близкое к стационарному, используют усреднение по промежуткам времени порядка нескольких десятков временных шагов ( ). Это эффективно увеличивает число участвующих в эксперименте частиц в 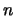раз. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... звезд ^3.2 Рассеянные звездные и шаровые скопления содержат соответственно 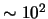и звезд и метод PP наиболее активно используется для моделирования этих систем. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... преимуществ ^3.3 Прежде всего силы определяются с такой же точностью, что и арифметическая точность ЭВМ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... частоту ^3.4 Поскольку в определение 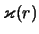входит производная 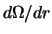, величину 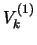необходимо предварительно сгладить, вычислить 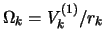, а затем и . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
...218]^3.5 Цель этих экспериментов заключалась, в частности, в проверке условия устойчивости диска (2.4.21). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
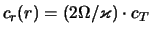... ^3.6 Диск, находящийся на границе устойчивости относительно мелкомасштабных возмущений ( 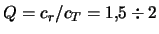, имеет 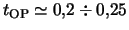, что, как видим, недостаточно для стабилизации глобальной бар-моды. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... звезд ^3.7 Отметим, что в рамках обсуждаемых экспериментов рассматривалась особенность в распределении ГМО -- кольцо повышенной плотности в области 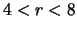(кпк) [72]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... бар-мода ^3.8 В самых внутренних областях некоторых галактик наблюдаются газовые (молекулярные) бары. Большая полуось этих структур составляет пк, что существенно меньше по сравнению с типичными звездными барами [301,302]. Причем молекулярные ядерные бары наблюдаются как в системах со звездным баром, так и в галактиках без бара. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... газа ^4.1 Обобщение на случай давления излучения см. [463], pазд.5.3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... вид ^4.2 Обсуждение модели тонкого диска и ее обобщение можно найти в моногpафии Гоpькавого и Фpидмана [185]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
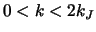...^4.3 В действительности этот интервал может быть несколько уже, поскольку при 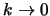нарушается ВКБ-приближение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... членов ^4.4 Если в двумеpной модели фоpмально положить 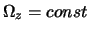, то она будет описывать тpехмеpную динамику частного класса возмущений, не имеющих попеpечной к плоскости диска компоненты волнового вектоpа. Пpи этом под 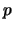, , 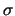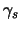следует подpазумевать не повеpхностные, а объемные давление, плотность, показатель адиабаты. Hа это указал В.В. Мусцевой. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... необычным ^4.5 В аналогичной по постановке плоской задаче возмущенное давление 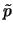является непрерывным при переходе через поверхность разрыва скорости [327]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
...eq4.5.18)]^4.6 Такая зависимость проявляется в следующем за (4.5.22) порядке: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
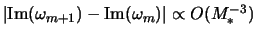... галактик ^4.7 Гипотеза об ответственности гидродинамических неустойчивостей в газовом диске за возбуждение спирального узора галактик была сформулирована А.М.Фридманом в 1972 г. Конкретные соображения о гидродинамическом механизме возбуждения спиралей и месте его локализации в галактиках были высказаны в работе [50]. Позднее были изучены гидродинамические неустойчивости в трехмерных моделях гравитирующей среды [345-348] и газовом диске [351,353]. Проведенное затем экспериментальное исследование центробежной неустойчивости на установках с вращающейся "мелкой водой" [354,355] позволило в конечном счете сформулировать гидродинамическую концепцию происхождения спирального узора плоских галактик (см. гл. 6). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... заметным ^4.8 Так, для двухрукавных возмущений при 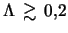величина 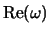меньше получаемой из (4.5.21) на 3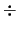0 40%. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... Галактике ^4.9 Заметим также, что плотное кольцо газа возникает в численных газодинамических моделях с баром [326] и в вязких осесимметричных моделях диска [360]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
...)^4.10 В работах [362,363] обсуждаются возможные методики и трудности наблюдательного определения параметра . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
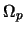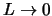... ^4.11 Этот фактор и затрудняет нахождение низкочастотной моды, поскольку в разрывной модели этой неустойчивости нет. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
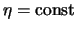... ^4.12 Такой подход аналогичен рассмотренному в разд. 5.2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... волны ^4.13 В работе Коваленко и Леви [394] в рамках аналитического подхода рассмотрено сверхзвуковое течение через потенциальную яму с установлением стационарной при определенных условиях (вид потенциала и параметры течения) ударной волны в области втекания газа в яму. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... т.п.^5.1 При таком подходе вполне уместна аналогия с падающим орбитальным спутником, попавшим в верхние слои атмосферы Земли. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... виде ^5.2 В литературе очень часто используются выражения типа (5.1.6), (5.1.9), (5.1.15), 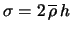и т.п., различающиеся коэффициентами порядка единицы, что связано с различием в усреднении по 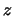-координате. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... АД ^5.3 Впервые такого рода решения были получены в работе [415]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... книги ^5.4 Изменение темпа истечения вещества из оптического компонента в ТДС может быть вызвано динамическими неустойчивостями в звезде [131,414,418-420]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... энергии ^5.5 В стационарной модели полная светимость диска определяется половиной гравитационной энергии падающего вещества. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
...^5.6 Лианг [430] построил свои модели в цилиндрической системе координат . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .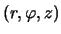
... вязкостью ^5.7 Речь идет о физической вязкости, но обычно используемые численные схемы обладают также численной вязкостью. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... волнами ^5.8 См. подробнее п. 5.2.3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... адиабаты ^5.9 В связи с выбором величины показателя адиабаты следует помнить, что значению в трехмерном случае соответствует 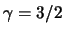в двумерных моделях (п. 4.1.1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... уравнению ^5.10 Небольшие различия в числовых коэффициентах у разных авторов связаны со способом усреднения по 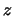-координате исходных уравнений. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... газовому ^5.11 Такую вязкость называют магнитной. Это связано с тем, что турбулентное динамо генерирует магнитное поле 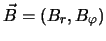, причем 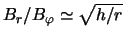и магнитное давление сравнимо с газовым. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
...fig5.16)^5.12 Здесь мы полагаем, что диск покоится, а движутся наружные области. Обратный переход производится обычным доплеровским преобразованием частоты. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... вектору ^5.13 Другими словами, вдоль поверхности разрыва газ убегает от волны быстрее, чем она его догоняет. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
...^5.14 Случай 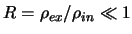наиболее интересен в приложении к дисковой аккреции на замагниченные компактные объекты, где существует проблема проникновения вещества в магнитосферу и плотность его там существенно ниже по сравнению с плотностью диска. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... уравнение ^5.15 В пределе 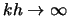это уравнение рассмотрено в работе [473], а для -- в [150]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... Папалойзу-Прингла ^5.16 Данный пункт написан совместно с В.В. Мусцевым. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... диски ^5.17 См. п. 5.1.6. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... величине ^5.18 Как показывает численное решение, плотность потока углового момента возмущений везде в диске направлена наружу. Это является отражением фундаментального принципа Ле-Шателье -- неустойчивые спиральные моды отводят наружу угловой момент вещества, аккрецирующего и тем самым высвобождающего гравитационную энергию. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... гармоник ^5.19 Суперпозиция неустойчивых мод с большим инкрементом, как правило, невозможна, поскольку наиболее быстро растущая мода на нелинейном этапе "переключает на себя" энергетический источник неустойчивости. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... тяжести ^5.20 В физике плазмы их называют диффузионными, перестановочными. Тяжелая жидкость над легкой, холодная над горячей, плазма над магнитным полем -- все это примеры развития данного типа неустойчивостей. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... системе ^5.21 Данный резонанс хорошо известен в небесной механике в ограниченной задаче трех тел. Примерами являются особенности движения астероидов в системе Солнце-Юпитер и некотоpые особенности структуры колец Сатурна с учетом спутников планеты. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... случае ^6.1 Ширину резонансной области мы не вычисляем, поскольку, как будет видно из приведенных ниже оценок, максимальный инкремент исследуемой неустойчивости порядка или меньше обратного времени радиального сноса пакета спиральных гравитационных волн [453]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
...496]^6.2 Аналогичный подход позволил развить теорию дрейфового движения заряженных частиц в магнитном поле посредством усреднения их реального движения по "быстрой" фазе ларморова вращения. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... гидродинамическим)^6.3 Сходная идея высказывалась А.М.Фридманом [503], объяснявшим многоярусность спиральной структуры -- различное число рукавов в различных областях диска по 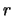-- тем, что в этих областях существуют различные условия для предпочтительного развития той или иной неустойчивости. Каждая из этих неустойчивостей характеризуется своей зависимостью максимального инкремента от номера азимутальной моды 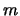, что и приводит к различным видам спиральной структуры в разных областях системы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .