Астронет > Закон Ампера

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Закон Ампера

Закон взаимодействия постоянных токов. Установлен А.Ампером в 1820. Согласно закону Ампера, сила $dF_{1\to2}$ , действующая со стороны одного элементарного "отрезка тока" $I_1d\vec l_1$ на другой $I_2d\vec l_2$ , убывает обратно пропорционально квадрату расстояния между ними $\vec r_{12}$ и в среде с магнитной проницаемостью $\mu$ . может быть представлена в виде
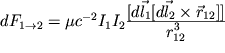$dF_{1\to 2}=\mu c^{-2}I_1 I_2{\displaystyle \lbrack d\vec l_1\lbrack d\vec l_2\times\vec r_{12}\rbrack\rbrack\over\displaystyle r_{12}^3}$ . (1)

Здесь использована Гаусса система единиц, с - скорость света в вакууме. Входящие в (1) элементарные отрезки токов являются частями замкнутых контуров, поскольку постоянные электрические токи всегда чисто соленоидальные (вихревые). Поэтому закон Ампера в форме (1) имеет лишь вспомогательный смысл, приводя к правильным (подтверждаемым на опыте) значениям силы только после интегрирования (1) по замкнутым контурам $l_1$ и $l_2$ .

Например, в общем случае элементарные силы между двумя отрезками токов оказываются невзаимными: $dF_{1\to 2}\neq dF_{2\to 1}$ однако при переходе к замкнутым контурам эта невзаимность устраняется. Из закона Ампера следует, в частности, что два прямых провода с токами $I_1$ и $I_2$ , текущими параллельно или антипараллельно друг другу на расстоянии d, соответственно притягиваются или отталкиваются с силой (на единицу длины), равной $F_{1\to 2}=F_{2\to 1}=\pm 2\mu I_1 I_2/c^2d$ . А два плоских контура с токами $I_1$ и $I_2$ на расстояниях, существенно превышающих их размеры, взаимодействуют между собой как два магнитных диполя и т. д. Из законов Ампера и Био-Савара вытекает выражение для силы, действующей на ток в заданном внешнем магнитном поле $\vec B=\mu\vec H$ ( $\vec H$ - напряженность магнитного поля, $\vec B$ - магнитная индукция), $d\vec F={\displaystyle 1\over\displaystyle c}I\lbrack d\vec l\times\vec B\rbrack$ . Отсюда в случае произвольно распределенных токов с объемной плотностью $\vec j=I\Delta\vec l/ \Delta V$ для силы на единицу объема $\vec f=\Delta\vec F/ \Delta V$ получается
$\vec f={\displaystyle 1\over\displaystyle c}\lbrack\vec j\times\vec B\rbrack$ . (2)

Величину (2) называют силой Ампера, а в случае конвективного тока, обусловленного движением заряженных частиц, $\vec j=\rho\vec v$ ( $\vec v$ - скорость, $\rho$ - объемная плотность заряда), она известна как сила Лоренца.

Иногда законом Ампера называется интегральное соотношение $\oint\limits_C \vec Hd\vec l=4\pi\cdot\vec I/c$ , где - полный ток, протекающий через поверхность, ограниченную замкнутым контуром С. Это соотношение аналогично теореме Гаусса в электростатике.

"Физическая Энциклопедия"/Phys.Web.Ru
Глоссарий Astronet.ru

L | R | А | Б | В | Г | Д | Е | Ж | З | И | Й | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Э | Ю | Я

Публикации с ключевыми словами: электричество - электрический ток - закон Ампера Публикации со словами: электричество - электрический ток - закон Ампера
См. также: Газовый разряд Вакуумный пробой Аномальное сопротивление плазмы Барионий Теорема Ампера Ампер

Обсудить эту публикацию

Версия для печати