args[0]=message
args[1]=DB::DB::Message=HASH(0x4538d00)
Re: Опыт Майкельсона и опыт Довженко
6.01.2014 17:27 | А.П. Васи
Собственно по теме
----------------------------------------------------------
http://sceptic-ratio.narod.ru/fi/es10.htm
\\\Опыт Ипполита Луи Физо (1819 1896), проведенный в 1851 г. и повторенный Майкельсоном в 1886 г., касался определения скорости света в движущейся среде. Упрощенная схема эксперимента выглядит как показано на .... 16, взятой из книги [17, с. 99].
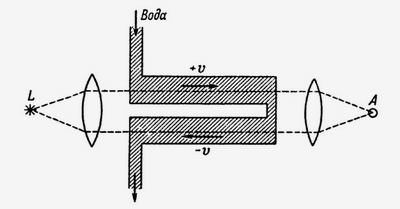
.... 16. Свет от источника L , разделяясь на два луча, проходит через трубу, по которой течет вода со скорость u. Из-за разности хода лучей в точке А появляется интерференционные полосы, которые можно сдвинуть, если изменить направление скорости u. По идее, результирующая скорость должна находиться по элементарной формуле сложения двух скоростей: V = c' u, где c' = c/n скорость света в среде с коэффициентом преломления n. Однако эксперимент показал, что эта формула не пригодна для расчета V.
Напомним, если скорость света в пустоте обозначить через c, то в среде с показателем преломления n она уменьшится: c' = c/n. В воздухе, как и в вакууме, она равна c' = c =300 000 км/с, так как для воздуха показатель преломления n близок к единице; для воды n = 1,33 и c' = 225 000 км/с, а для алмаза n = 2,42 и c' = 124 000 км/с. Получается, чем плотнее среда, тем меньше скорость света (плотность алмаза в 3,5 раза выше воды). В акустике, в общем, наблюдается обратная зависимость. Если в воздухе звук распространяется со скоростью 331 м/с, то в воде 1482 м/с, а в стали 6000 м/с. Однако зависимость скорости акустической волны от плотности среды не столь однозначна и зависит от строения вещества (см. табл. 3 Введение в акустику).
Фуко показал, когда водная среда начинает перемещаться, скорость света в ней находится по "релятивистской" формуле сложения двух скоростей:
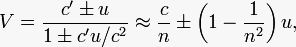
где u = 7 м/c, при которой не образуется турбулентных .... На одном участке трубы скорость движения воды u совпадает со скоростью c' и тогда в формуле фигурирует, на друго участке не совпадает и тогда ставится "".
Но ни о какой "релятивистской" трактовке последней формулы в середине XIX века не могло быть и речи. Интерпретации поддавалась ее приближенное значение, за которым скрывалось более сложная зависимость результирующей скорости V от длины волны светового излучения. Выражение стоящее в скобках называлось коэффициентом увлечения, который вывел и объяснил Огюстен Жан Френель (1788 1827) еще в 1818 году, после эксперимента, проведенного Домиником Франсуа Жаном Араго (1786 1853).
Араго экспериментировал с движущейся стеклянной призмой, измеряя при этом угол аберрации. Он рассчитывал, что два знакомых нам вектора скорости будут складываться и вычитаться обычным образом: V = c' u. Тогда, в соответствии с логикой эксперимента, должен был измениться угол аберрации. Однако с точностью до одной угловой секунды величина α = 20,45", найденная Дж. Брэдли, не менялась.
Цель эксперимента можно было сформулировать иначе и решать обратную задачу: как изменится показатель преломления призмы, находящейся на Земле, движущейся со скоростью 30 км/с, если через призму пропускать свет от неподвижной звезда. Тогда отрицательное заключение из этой постановки задачи выглядит так: показатель преломления призмы не меняется.
Френель принял, что световые волны носят продольный характер, как и акустические волны (поперечный характер световых волн был установлен им в 1821 году). Скорость звука в том или ином веществе, как мы уже знаем (Введение в акустику), зависит от плотности вещества. Избыток плотности возникает в результате различного рода возбуждений среды, например, воздушных и водных вихрей. Если акустические волны пропускать через движущийся со скоростью u вихрь, то их звуковая скорость внутри вихря будет реагировать на избыточную плотность в соответствии с "релятивистской" формулой. Кажется, что в вихре кружится весь заключенный в нем воздух и переносится вместе с вихрем. Если так, то результирующая скорость определялась бы по "классической" формуле сложения скоростей, но этого не случилось. На высоком формально-теоретическом уровне Френелю удалось провести параллель между оптическими и акустическими явлениями. Он показал, что увлечению подвергается лишь избыток плотности эфира в материальных телах по сравнению с плотностью эфира в открытом космосе.
Волновая теория Френеля, объясняющая целый комплекс оптических проблем, включая дифракцию и поляризацию, безмятежно господствовала при и его жизни и затем еще без малого два десятка лет после его смерти. Французская школа оптиков, прежде всего, в лице Араго, Френеля, Фуко и Физо, явно доминировала в мире. Англичане, вечные конкуренты французов, с завистью взирали на успехи своих противников не только в научной сфере, но также культурной, политической и военной.
Френель вывел коэффициент частичного увлечения, оперируя двумя характеристиками эфира, определяющими скорость света. Это его упругость, которая оставалась неизменной для движущихся сред, и его варьируемой плотности. Англичанин Джордж Габриэль Стокс (1891 1903) в середине 1840-х годов впервые высказал идею полного увлечения эфира движущимися объектами такими, например, как наша планета. При этом он опирался на третью механическую характеристику эфира вязкость. В 1849 году он опубликовал фундаментальную работу О теории внутреннего трения в движущихся жидкостях и о равновесии и движении упругих твёрдых тел, в которой получил знаменитое дифференциальное уравнение для описания движения вязких жидкостей.
Стокс считал, что Земля целиком увлекает эфир не только внутри своего объема, но и далеко за пределами своей поверхности. Как высоко простирается слой увлекаемого планетой эфира неизвестно. Миллер, пытаясь измерить скорость эфирного ветра, старался подняться вместе с интерферометр как можно выше: быть может, там высоко в горах или на высоте полета дирижабля дует ветер. Эксперимент Физо 1851 года был хорош как раз тем, что убедительно доказывал не состоятельность теории Стокса и справедливость теории Френеля.
В 1868 году всем известный англичанин, Джеймс Клерк Максвелл (18311879), сам проделал опыт, аналогичный опыту Физо. Однако, по итогам экспериментирования он вынужден был признать победу за теорией Френеля. Так как эксперимент Физо касался эффекта первого порядка по β, Максвелл высказал предположение, что эффект по β², возможно, даст о себе знать в будущем, когда физики научатся измерять столь малые величины.
Следующий за этим эксперимент, проведенный англичанином Джорджем Бидделем Эйри (18011892) в 1871 году по измерению звездной аберрации при наблюдении через телескоп, заполненный водой, также подтвердил правоту Френеля. Наконец, эксперимент 1886 года, осуществленный Майкельсоном и Морли, по схеме близкой к экспериментальной установке Физо 1851 года, еще раз доказали верность теории частичного увлечения эфира. Вот, как об этом говорил Майкельсон на юбилейной конференции 1927 года:
В 1880 году я задумался над возможностью измерения оптическим способом скорости v движения Земли в Солнечной системе. Ранние попытки обнаружить эффекты первого порядка основывались на идее движения системы сквозь стационарный эфир. Эффекты первого порядка пропорциональны v/c, где c скорость света. Исходя из представлений о любимом старом эфире (который теперь заброшен, хотя я лично еще его придерживаюсь), ожидалась одна возможность, а именно, что аберрация света должна быть различной для телескопов, заполненных воздухом или водой. Однако эксперименты показали вопреки существующей теории, что такой разницы не существует.
Теория Френеля первая объяснила этот результат. Френель предположил, что вещество захватывает эфир, частично (увлечение эфира), придавая ему скорость v, так что v' = kv. Он определил k коэффициент Френеля через показатель рефракции n: k = (n² 1)/n². Этот коэффициент легко получается из отрицательного результата следующего эксперимента.\\\
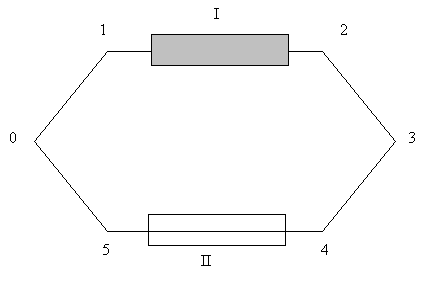 \\\
\\\
--------------------------------------------------
- Опыт Майкельсона и опыт Довженко
(В. Ш. Янбиков,
5.01.2014 23:55, 10.2 КБайт, ответов: 10)
Уважаемые коллеги. Прошу ознакомиться с опытом Довженко А.И.... - Re: Опыт Майкельсона и опыт Довженко
(А.П. Васи,
6.01.2014 11:52, 2.1 КБайт)
Собственно то что Вы пишите это и коню понятно.... - Re: Опыт Майкельсона и опыт Довженко
(А.П. Васи,
6.01.2014 13:18, 1.1 КБайт)
Вы если хотите что-то сказать... - >> Re: Опыт Майкельсона и опыт Довженко
(А.П. Васи,
6.01.2014 17:27, 9.0 КБайт)
Собственно по теме----------------------------------------------------------http://sceptic-ratio.narod.ru/fi/es10.htm... - Re: Опыт Майкельсона и опыт Довженко
(А.П. Васи,
6.01.2014 17:37, 1.5 КБайт)
И если нечего делать... - Re: Опыт Майкельсона и опыт Довженко
(А.П. Васи,
7.01.2014 22:13, 2.7 КБайт, ответов: 1)
Более простое и понятное объяснение.... - Re[2]: Опыт Майкельсона и опыт Довженко
(В. Ш. Янбиков,
11.01.2014 22:39, 102 Байт)
Уважаемый А.П. Васи. Спасибо за лекцию.... - Re: Опыт Майкельсона и опыт Довженко
(А.П. Васи,
11.01.2014 23:37, 6.9 КБайт)
Собственно... - Re: Опыт Майкельсона и опыт Довженко
(А.П. Васи,
11.01.2014 23:51, 1.0 КБайт)
http://lenta.ru/news/2014/01/10/electricsailuranus/ Движение электрического паруса... - Re: Опыт Майкельсона и опыт Довженко
(А.П. Васи,
16.01.2014 0:52, 2.1 КБайт)
Собственно я не понаслышке... - Re: Опыт Майкельсона и опыт Довженко
(А.П. Васи,
16.01.2014 22:53, 3.2 КБайт)
Естественно на плохой основе невозможно сделать ничего достаточно качественного....