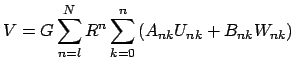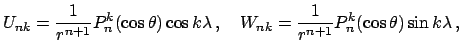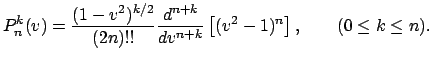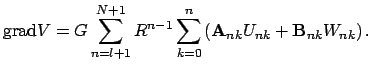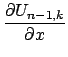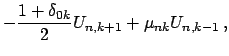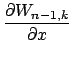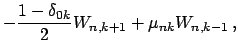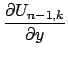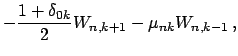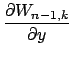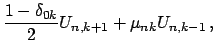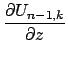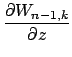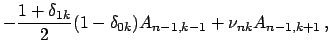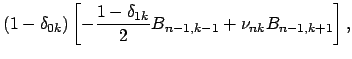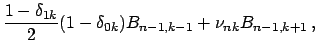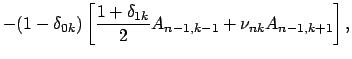 |
Астронет: К. В. Холшевников/Коуровка Простейшая форма представления градиента гравитационного потенциала небесных тел http://variable-stars.ru/db/msg/1202453/node3.html |
2. Гравитационное поле невращающегося тела
Рассмотрим тело 
, неподвижное относительно декартовой системы
координат 
. Его гравитационный потенциал 
может
быть представлен рядом Лапласа
по шаровым функциям
Здесь
- сферические координаты, 
-
произведение гравитационной постоянной на массу , 
-
масштабный фактор, 
и 
- безразмерные коэффициенты
Стокса, постоянные для данного тела. В общем случае 
, 
,
но иногда интерес представляет часть ряда (1), так что мы не
придерживаемся этих значений 
, ограничивая их лишь неравенствами
,
.
Хорошо известно, что градиент шаровой функции сам является шаровой функцией, а ее порядок повышается на единицу [2]:
Остается только выразить (также безразмерные) компоненты
, 
векторов
через
. Кратчайший
путь - использование слегка модифицированных соотношений [1]
где
- символ Кронекера, 
, 
.
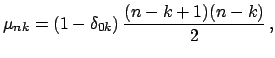
Сравнение (4) и (5) дает компоненты
векторов
как линейные комбинации
при 
, 
при 
:
при
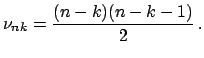
Замечание. Обычно считают 
и
вне пределов суммирования равными нулю. В частности,
Используя (6), мы можем не учитывать (7), так как все соответствующие коэффициенты обращаются в нуль.
Стоит заметить также, что 
, а если начало 
системы
отсчета 
помещено в центр масс , то
<< 1. Введение | Оглавление | 3. Среднеквадратическая нормализация >>