 |
Астронет: В. В. Нестеров/ГАИШ Стандарт основных вычислений астрономии http://variable-stars.ru/db/msg/1178709/node18.html |
1.14. И это тоже Ньюкомб
Теперь необходимо вычислить значения всех этих углов поворота. Это сделал Ньюкомб на основе
исходных данных и результатов наблюдений, известных 100 лет назад. С новыми значениями масс
Солнца, Земли, Луны и планет был выполнен пересчет. Нашли, чему равны 
и 
. Из
сферических треугольников получили 
, 
, 
, из тех же треугольников нашли
простые соотношения для прецессионных параметров Ньюкомба-Андуайе 
, 
, 
.
Поскольку исходные формулы для величин и являются полиномами по времени, то и формулы
для , , получены в том же виде.
Фундаментальная эпоха 
совпадает со стандартной эпохой J2000.0, 
- эпоха
даты, 
- любая фиксированная эпоха.
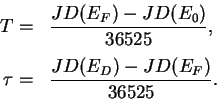
Величины 
и 
, как нетрудно видеть, измеряются в юлианских столетиях.
Повторю еще раз, что формулы справедливы на конечном интервале времени, две-три сотни лет. Экстраполяция здесь не приемлема.
Вот это одно преобразование, со значениями малых углов поворота , , - самое
важное, может заменить все остальные соотношения.
Прежде применяли числа Крюгера 
и 
при определении
прецессии по прямому восхождению 
и склонению 
,
этот способ для звезд с
дает точность
, а вот для близполюсных звезд точность гораздо хуже,
поэтому старый способ необходимо исключить. Это следует и из
постановления МАС1976: применять точные формулы и использовать
прямоугольные координаты.
В следующий раз рассмотрим вопрос о совместном учете прецессии и собственных движений.
<< 1.13. Между эклиптикой и ... | Оглавление | 1.15. Когда разгуляется >>