Astronet Астронет:  Научная Сеть/НС Колебания и волны
http://variable-stars.ru/db/msg/1175791/page9.html

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

Быстрые колебания.

Если $\omega \gg \omega _{0} ,$ то период вынужденных колебаний $T = {\displaystyle {\displaystyle 2\pi } / {\displaystyle \omega }}$ мал. Это означает, что масса $m$ испытывает действие лишь внешней силы $F(t),$ а сила упругости $ks$ и вязкого трения $\Gamma \dot {\displaystyle s}$ малы. Действительно, за половину короткого периода колебаний, когда масса движется в одном направлении, она не успевает набрать как заметную скорость $\dot {\displaystyle s},$ так и сместиться на достаточною величину $s$ от положения равновесия. Поэтому в уравнении (2.10) можно опустить члены, содержащие $s$ и $\dot {\displaystyle s},$ и записать его в другом приближенном виде:

$ \ddot {\displaystyle s} = {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle m}}}\sin \omega t. $(2.14)

Интегрируя это уравнение два раза, находим закон движения колеблющейся массы:

$ s(t) = - {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle m\omega ^{2}}}}\sin \omega t = {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle m\omega ^{2}}}}\sin (\omega t - \pi ). $(2.15)

Из (2.15) следует, что смещение по отношению к внешней силе запаздывает по фазе на $\pi (\varphi _{0} = - \pi ),$ а амплитуда, как мы и предполагали, убывает с увеличением частоты.

В схеме, изображенной на рис. 2.2, в таком режиме левый подвижный конец пружины и масса $m$ всегда движутся в противоположных направлениях:

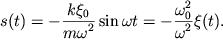$ s(t) = - {\displaystyle \frac{\displaystyle {\displaystyle k\xi _{0} }}{\displaystyle {\displaystyle m\omega ^{2}}}}\sin \omega t = - {\displaystyle \frac{\displaystyle {\displaystyle \omega _{0}^{2} }}{\displaystyle {\displaystyle \omega ^{2}}}}\xi (t). $(2.16)

По абсолютной величине смещение массы $m$ в ${\displaystyle {\displaystyle \omega ^{2}} / {\displaystyle \omega _{0}^{2} }} \gg 1$ раз меньше смещения левого конца пружины, т.е. практически не будет заметным.

Резонансный режим.

Если частота $\omega \approx \omega _{0} ,$ то вынужденные колебания происходят на собственной частоте колебаний. Это означает, что

$ \ddot {\displaystyle s} + \omega _{0}^{2} s = 0. $(2.17)

Следовательно, уравнение (2.10) при учете (2.17) примет вид:

$ 2\delta \dot {\displaystyle s} = {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle m}}}\sin \omega _{0} t. $(2.18)

Интегрируя его, получаем выражение для смещения:

$ s(t) = {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle 2\delta m\omega _{0} }}}\sin (\omega _{0} t - {\displaystyle {\displaystyle \pi } / {\displaystyle 2}}). $(2.19)

Последнее выражение удобно переписать в виде

$ s(t) = {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle k}}}Q\sin (\omega _{0} t - {\displaystyle {\displaystyle \pi } / {\displaystyle 2),}} $(2.20)

где $Q = {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle \delta T}}}$ - добротность маятника. Если добротность $Q \gg 1,$ то амплитуда колебаний может во много раз превышать амплитуду медленных квазистатических колебаний (ср. с (2.12)). Поэтому такой режим называется резонансным.

Велики также амплитуды скорости и ускорения. Поскольку скорость $\dot {\displaystyle s},$ как следует из (2.18), изменяется в фазе с внешней силой, то с энергетической точки зрения это весьма благоприятно для "подкачки" энергии в колебательную систему. Работа внешней силы за период колебаний равна:

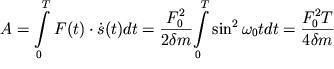$ A = {\displaystyle \int\limits_{0}^{T} {\displaystyle F(t) \cdot \dot {\displaystyle s}(t)dt = {\displaystyle \frac{\displaystyle {\displaystyle F_{0}^{2} }}{\displaystyle {\displaystyle 2\delta m}}}} }{\displaystyle \int\limits_{0}^{T} {\displaystyle \sin ^{2}\omega _{0} tdt = {\displaystyle \frac{\displaystyle {\displaystyle F_{0}^{2} T}}{\displaystyle {\displaystyle 4\delta m}}}} } $(2.21)

и значительно превосходит работу этой силы в обоих рассмотренных выше режимах. Такая большая работа необходима для компенсации значительных потерь из-за силы вязкого трения.

Для большей наглядности последнего результата обратимся к схеме с подвижным левым концом пружины, где, как это видно из решения (2.20),

$ s(t) = \xi _{0} Q\sin (\omega _{0} t - {\displaystyle {\displaystyle \pi } / {\displaystyle 2)}}. $(2.22)

Амплитуда смещения правого конца пружины в $Q$ раз превосходит амплитуду смещения левого конца. При прохождении массой $m$ положения равновесия $s = 0,$ когда ее скорость максимальна, левый конец пружины смещен на максимальную величину $\xi _{0}$ в направлении скорости движущейся массы. В этот момент времени мощность силы упругости пружины имеет максимально возможное положительное значение при заданной величине $\xi _{0} .$ В последующие моменты времени эта мощность будет оставаться положительной, что, естественно, обеспечивает наиболее эффективную передачу энергии движущемуся с трением телу.

Если сила (2.5) меняется с произвольной частотой $\omega ,$ то амплитуда $s_{0}$ и фаза $\varphi _{0} ,$ входящие в решение (2.7), могут быть найдены, как было сказано выше, подстановкой решения (2.7) в уравнение (2.10). Такую подстановку можно осуществить наиболее просто, если воспользоваться методом комплексных амплитуд, широко применяемым в различных областях физики: теории колебаний, теории волн, электромагнетизме, оптике и др.

Метод комплексных амплитуд.

Если в формуле Эйлера (1.53): $e^{i\varphi } = \cos \varphi + i\sin \varphi$ под $\varphi$ понимать фазу гармонических колебаний

$ \varphi = \omega t + \varphi _{0} , $(2.23)

то каждому такому колебанию $s(t)$ можно поставить в соответствие комплексное число

$ \hat {\displaystyle s}(t) = s_{0} e^{i\varphi } = s_{0} e^{i\varphi _{0} }e^{i\omega t} = s_{0} \cos (\omega t + \varphi _{0} ) + is_{0} \sin (\omega t + \varphi _{0} ) $(2.24)

Из (2.24) видно, что решение (2.7) является мнимой частью комплексного выражения:

$ s(t) = s_{0} \sin (\omega t + \varphi _{0} ) = Im\hat {\displaystyle s}_{0} e^{i\omega t}, $(2.25)

где $\hat {\displaystyle s}_{0} = s_{0} e^{i\varphi _{0} }$ - комплексная амплитуда, которая несет информацию об амплитуде $s_{0}$ и начальной фазе $\varphi _{0}$ колебаний. Надо отметить, что метод комплексных амплитуд является, фактически, аналитическим выражением метода векторных диаграмм. Если в последнем методе колебание с частотой $\omega$ полностью задается вектором ${\displaystyle \bf s_{0}} ,$ то в методе комплексных амплитуд колебание задается числом $\hat {\displaystyle s}_{0}$ на комплексной плоскости. Поскольку с комплексными числами удобно и просто производить математические операции, то мы используем это обстоятельство для получения решения уравнения вынужденных колебаний (2.10).

Назад| Вперед

Rambler's Top100 Яндекс цитирования