Астронет > Колебания и волны

Астронет: Научная Сеть/НС Колебания и волны
http://variable-stars.ru/db/msg/1175791/page25.html

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

Скорость волн в толстом стержне.

Пусть вдоль оси толстого стержня (оси х) распространяется продольная волна, при этом колеблются элементы стержня, находящиеся вблизи его оси.

Один из таких элементов показан на рис. 4.27. Под действием нормального напряжения $\sigma _{1}$ относительное удлинение $\varepsilon _{1}$ определяется первым уравнением (1.27), приведенным в лекции по деформации твердого тела:

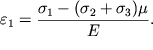$\varepsilon _{1} = {\displaystyle \frac{\displaystyle {\displaystyle \sigma _{1} - (\sigma _{2} + \sigma _{3} )\mu }}{\displaystyle {\displaystyle E}}}.$

(4.78)

Это уравнение отражает тот факт, что при удлинении элемента $dx,$ изображенного на рис. 4.27, площадь его поперечного сечения уменьшается (связь продольной и поперечной деформаций определяется коэффициентом Пуассона $0 \lt \mu \lt 1 / 2$ ). Этот элемент потянет к оси стержня окружающие его элементы, развивая напряжения $\sigma _{2}$ и $\sigma _{3}.$ Эти элементы (лежащие между плоскостями x = const и x + dx = const) начнут приходить в движение: сначала - находящиеся вблизи оси стержня, а затем и элементы, близкие к поверхности. 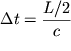Через время $\Delta t = {\displaystyle \frac{\displaystyle {\displaystyle L / 2}}{\displaystyle {\displaystyle c}}}$ ( $L$ - поперечный размер стержня, с - скорость распространения возмущения) все элементы сместятся, и напряжения $\sigma _{2}$ и $\sigma _{3}$ исчезнут.

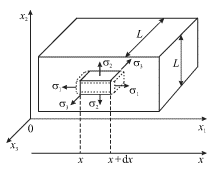Рис. 4.27.

Если длительность $\tau _{и}$ импульса, распространяющегося вдоль оси стержня, велика, так что $\tau _{и} \gg \Delta t = {\displaystyle \frac{\displaystyle {l}}{\displaystyle {\displaystyle 2c}}},$ то в (4.78) можно не учитывать $\sigma _{2}$ и $\sigma _{3}.$ Скорость такого длинного импульса будет определяться формулой (4.77). Такой режим можно реализовать, если

$L \ll c\tau _{и}.$

(4.79)

Условие (4.79) означает, что поперечный размер стержня $L$ значительно меньше длины импульса. Такой стержень можно считать тонким. Если речь идет о гармонической волне, распространяющейся вдоль стержня, то условие (4.79) имеет вид

$L \ll \lambda,$

(4.80)

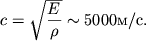где $\lambda = cT$ - длина волны, $Т$ - период колебаний. Так, например, для стального стержня $c = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle E}}{\displaystyle {\displaystyle \rho }}}} \sim 5000 м/с.$ При частоте $\nu = 5000 Гц,\; \lambda = c / \nu \sim 1 м,$ поэтому стержни с поперечным размером $L\sim 1 см$ могут считаться тонкими.

Если длительности импульса $\tau _{и} \ll \Delta t = {\displaystyle \frac{\displaystyle {l}}{\displaystyle {\displaystyle 2c}}}$ (стержень толстый), то в (4.78) следует учесть $\sigma _{2}$ и $\sigma _{3}$ . Чтобы найти связь $\varepsilon _{1}$ и $\sigma _{1},$ вместе с уравнением (4.78) запишем аналогичные для $\varepsilon _{2}$ и $\varepsilon _{3}$ и сложим все три уравнения:

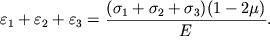$\varepsilon _{1} + \varepsilon _{2} + \varepsilon _{3} = {\displaystyle \frac{\displaystyle {\displaystyle (\sigma _{1} + \sigma _{2} + \sigma _{3} )(1 - 2\mu )}}{\displaystyle {\displaystyle E}}}.$

(4.81)

Для краткости выкладок введем средние значения

$\varepsilon = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 3}}}(\varepsilon _{1} + \varepsilon _{2} + \varepsilon _{3} ); \quad \sigma = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 3}}}(\sigma _{1} + \sigma _{2} + \sigma _{3} ).$

Тогда (4.81) перепишется в виде

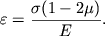$\varepsilon = {\displaystyle \frac{\displaystyle {\displaystyle \sigma (1 - 2\mu )}}{\displaystyle {\displaystyle E}}}.$

(4.82)

С учетом (4.82) уравнение (4.78) видоизменяется:

$\varepsilon _{1} + {\displaystyle \frac{\displaystyle {\displaystyle 3\mu \varepsilon }}{\displaystyle {\displaystyle 1 - 2\mu }}} = {\displaystyle \frac{\displaystyle {\displaystyle 1 + \mu }}{\displaystyle {\displaystyle E}}}\sigma _{1}.$

(4.83)

Если положить в толстом стержне $\varepsilon _{2} = \varepsilon _{3} = 0,$ то $\varepsilon = \varepsilon _{1} / 3,$ и искомая связь получится в виде:

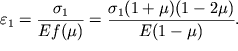$\varepsilon _{1} = {\displaystyle \frac{\displaystyle {\displaystyle \sigma _{1} }}{\displaystyle {\displaystyle Ef(\mu )}}} = {\displaystyle \frac{\displaystyle {\displaystyle \sigma _{1} (1 + \mu )(1 - 2\mu )}}{\displaystyle {\displaystyle E(1 - \mu )}}}.$

(4.84)

В этом случае связь деформации и напряжения определяется как модулем Юнга $Е,$ так и следующей функцией коэффициента Пуассона

$f(\mu ) = {\displaystyle \frac{\displaystyle {\displaystyle 1 - \mu }}{\displaystyle {\displaystyle (1 + \mu )(1 - 2\mu )}}}.$

(4.85)

Легко убедиться, что при любых возможных значениях коэффициента Пуассона $f(\mu ) \gt 1.$ Поэтому скорость продольной волны в этом случае

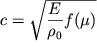$c = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle E}}{\displaystyle {\displaystyle \rho _{0} }}}f(\mu )}$

(4.86)

превышает скорость волны в тонком стержне. Величину $E \cdot f(\mu )$ обычно называют "модулем одностороннего растяжения".

Отметим, что наиболее сложен анализ для промежуточного случая, когда $L\sim \lambda.$ Для волн с такой длиной волны имеет место дисперсия (фазовая скорость гармонической волны зависит от ее частоты). Распределение амплитуды волны в поперечном сечении стержня вдоль осей $x_{2}$ и $x_{3}$ аналогично распределению амплитуды для шнура длиной $L$ со свободными концами при нормальном колебании. Стержень в этом случае выполняет роль волновода. При его плавном изгибании волна распространяется вдоль его оси.

Продольные волны переносят энергию, и для них справедливы все рассуждения и выводы, полученные для поперечных волн. Формально во все выражения для плотности энергии $w,$ вектора Умова $\bf J$ и др. следует вместо модуля сдвига $G$ подставить модуль Юнга $Е$ или $E \cdot f(\mu ).$ Предоставляем читателю проделать это самостоятельно.

Явления на границе двух сред.

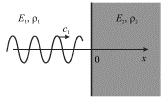
Рассмотрим подробнее прохождение продольной волны через границу раздела двух упругих сред при нормальном падении волны на эту границу.

Пусть продольная волна распространяется со скоростью $c_{1} = \sqrt {\displaystyle E_{1} / \rho _{1} }$ в среде с модулем Юнга $E_{1}$ и равновесной плотностью $\rho _{1}$ (рис. 4.28). Опыт показывает, что эта волна на границе раздела двух сред ( $х = 0$ на рисунке) частично отражается и частично проходит во вторую среду, которая характеризуется параметрами $E_{2}$ и $\rho _{2}.$ Следовательно, можем записать

1-я среда	2-я среда	(4.87)
(падающая + отраженная волна)	(прошедшая волна)
$s_{1} (x,t) = s_{01} \sin (\omega t - k_{1} x) + {\displaystyle s}'_{01} \sin (\omega t + k_{1} x)$	$s_{2} (x,t) = s_{02} \sin (\omega t - k_{2} x)$

Здесь $\omega$ - частота, $s_{01}, {\displaystyle s}'_{01}$ и $s_{02}$ - амплитуды падающей, отраженной и прошедшей волн соответственно, $k_{1} = \omega / c_{1}$ и $k_{2} = \omega / c_{2}$ - соответствующие волновые числа.

Рис. 4.28.

Чтобы найти соотношения между амплитудами трех волн, определяющие отражательную и пропускательную способность ("прозрачность") границы раздела, запишем два условия, которые должны выполняться на границе раздела при $х = 0.$

Первое - это условие неразрывности вещества:

$s_{1} (0,t) = s_{2} (0,t).$

(4.88)

Второе - равенство напряжений:

$\sigma _{1} (0,t) = \sigma _{2} (0,t), \; или \; E_{1} \varepsilon _{1} (0,t) = E_{2} \varepsilon _{2} (0,t).$

(4.89)

С учетом (4.87) из этих условий получаем:

$\begin{array}{l} s_{01} + {\displaystyle s}'_{01} = s_{02}, \\ - s_{01} E_{1} k_{1} + {\displaystyle s}'_{01} E_{1} k_{1} = - s_{02} E_{2} k_{2}. \\ \end{array}$

(4.90)

В акустике фундаментальным является понятие импеданса, или удельного волнового (акустического) сопротивления материала. Эта величина $z$ определяется как:

$z = {\displaystyle \frac{\displaystyle {\displaystyle сжимающее\; напряжение}}{\displaystyle {\displaystyle колебательная\; скорость}} = {\displaystyle \frac{\displaystyle {\displaystyle - \sigma }}{\displaystyle {\displaystyle v}}}}.$

(4.91)

Импеданс легко можно выразить через характеристики материала, воспользовавшись формулой (4.73):

$\varepsilon = {\displaystyle \frac{\displaystyle {\displaystyle \sigma }}{\displaystyle {\displaystyle E}}} = - {\displaystyle \frac{\displaystyle {\displaystyle v}}{\displaystyle {\displaystyle c}}}.$

(4.92)

Отсюда

$z = {\displaystyle \frac{\displaystyle {\displaystyle - \sigma }}{\displaystyle {\displaystyle v}}} = {\displaystyle \frac{\displaystyle {\displaystyle E}}{\displaystyle {\displaystyle c}}} = \rho c.$

(4.93)

С использованием этой величины и выражений для $k_{1}$ и $k_{2}$ условия (4.90) примут вид:

$\begin{array}{l} s_{01} + {\displaystyle s}'_{01} = s_{02} \\ - s_{01} z_{1} + {\displaystyle s}'_{01} z_{1} = - s_{02} z_{2}. \\ \end{array}$

(4.94)

Отсюда получаем искомую связь между амплитудами волн:

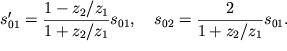${\displaystyle s}'_{01} = {\displaystyle \frac{\displaystyle {\displaystyle 1 - z_{2} / z_{1} }}{\displaystyle {\displaystyle 1 + z_{2} / z_{1} }}}s_{01}, \quad s_{02} = {\displaystyle \frac{\displaystyle {\displaystyle 2}}{\displaystyle {\displaystyle 1 + z_{2} / z_{1} }}}s_{01}.$

(4.95)

Для практических целей пользуются коэффициентами отражения $R$ и пропускания $Т,$ характеризующими отношение интенсивностей отраженной и прошедшей волн к интенсивности падающей волны. Эти коэффициенты получаются из (4.95) с учетом (4.65):

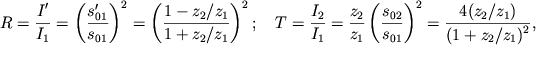$R = {\displaystyle \frac{\displaystyle {\displaystyle {\displaystyle I}'}}{\displaystyle {\displaystyle I_{1} }}} = \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle {\displaystyle s}'_{01} }}{\displaystyle {\displaystyle s_{01} }}}} \right)^{2} = \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle 1 - z_{2} / z_{1} }}{\displaystyle {\displaystyle 1 + z_{2} / z_{1} }}}} \right)^{2}; \quad T = {\displaystyle \frac{\displaystyle {\displaystyle I_{2} }}{\displaystyle {\displaystyle I_{1} }}} = {\displaystyle \frac{\displaystyle {\displaystyle z_{2} }}{\displaystyle {\displaystyle z_{1} }}}\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle s_{02} }}{\displaystyle {\displaystyle s_{01} }}}} \right)^{2} = {\displaystyle \frac{\displaystyle {\displaystyle 4(z_{2} / z_{1} )}}{\displaystyle {\displaystyle (1 + z_{2} / z_{1} )^{2}}}},$

(4.96)

где использовано то обстоятельство, что интенсивность бегущей волны (см. формулу (4.65))

$I = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}c\rho \omega ^{2}s_{0}^{2} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}z\omega ^{2}s_{0}^{2}$

(4.97)

зависит не только от амплитуды $s_{0}$ и частоты $\omega,$ но и пропорциональна акустическому сопротивлению $z.$ Следует отметить, что формулы (4.96) справедливы и для поперечных колебаний.

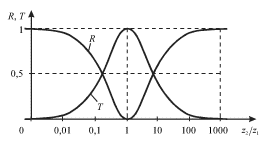
Из рисунка 4.29, на котором изображены зависимости (4.96), видно, что если $z_{1} = z_{2},$ отражения не происходит. Поэтому на практике, когда надо уменьшить отражение, стараются согласовать (сделать практически одинаковыми) волновые сопротивления двух сред.

Рис. 4.29.

Заметим также, что при $z_{2} \ll z_{1},$ как в случае свободного конца стержня ( $z_{2}$ - сопротивление воздуха), или $z_{2} \gg z_{1}$ (закрепленный конец), $R \approx 1,$ т.е. происходит практически полное отражение волны, что мы и использовали выше при рассмотрении отражения в этих предельных случаях.

Назад| Вперед