Астронет > Колебания и волны

Астронет: Научная Сеть/НС Колебания и волны
http://variable-stars.ru/db/msg/1175791/page23.html

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

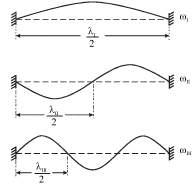
Для примера на рис. 4.14 изображены три возможные конфигурации шнура в момент времени, когда смещения элементов шнура максимальны. Колебания, соответствующие этим конфигурациям, являются нормальными колебаниями (модами), а частоты $\omega _{I}, \omega _{II}, \omega _{III}$ - нормальными частотами. Если действие внешней силы прекратится, то эти колебания будут продолжаться как собственные, пока не затухнут.

Рис. 4.14.

Условие (4.39) можно переписать в более наглядном виде, если перейти от частоты $\omega _{p}$ к длине волны $\lambda _{p} = 2\pi c_{0} / \omega _{p}$ :

$\ell = p{\displaystyle \frac{\displaystyle {\displaystyle \lambda _{p} }}{\displaystyle {\displaystyle 2}}}.$

(4.40)

Это условие означает, что при нормальных колебаниях на длине шнура должно укладываться целое число полуволн. Легко теперь видеть, что каждая из мод может быть возбуждена, если прикладывать силу нужной частоты к любому участку шнура, за исключением тех, которые совпадают с узлами данной моды.

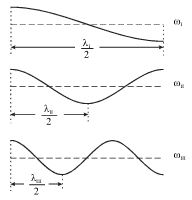
Видоизменим граничные условия и сделаем оба конца шнура свободными (привяжем их к натянутым легким нитям). Подсчитаем частоты вынуждающей силы, на которых возбуждаются стоячие волны (моды). Учтем, что после двух отражений импульс не меняет свою полярность, поэтому условие (4.40) останется прежним.

На рис. 4.15 показаны конфигурации мод для шнура со свободными концами. Видно, что при нормальных колебаниях на длине шнура также должно укладываться целое число полуволн, но таким образом, чтобы на концах шнура были пучности.

Рис. 4.15.

Закрепим теперь только левый конец шнура и будем двигать кронштейн с малой амплитудой $\xi _{0}.$ Условие оптимального возбуждения стоячих волн (мод) получается из тех соображений, что импульс обращается только при отражении от левого конца шнура. Для усиления импульса необходимо, чтобы левый конец в момент времени $t = \Delta t$ двигался вниз, проходя положение равновесия:

$\begin{array}{l} s(\Delta t) = \xi {\displaystyle }_{0}\sin (\omega \Delta t) = 0, \\ \dot {\displaystyle s}(\Delta t) = \xi _{0} \omega \cos (\omega \Delta t) = - \xi _{0} \omega. \\ \end{array}$

(4.41)

Поэтому частота \omega должна удовлетворять условию

$\omega _{p} \Delta t = (2p - 1)\pi,$

(4.42)

где $p = I, II, III, \ldots$

Отсюда

$\omega _{p} = {\displaystyle \frac{\displaystyle {\displaystyle \pi c_{0} }}{\displaystyle {\displaystyle 2\ell }}}(2p - 1).$

(4.43)

Последнее условие становится более наглядным, если перейти к длине волны $\lambda _{p}$ :

$\ell = (2p - 1){\displaystyle \frac{\displaystyle {\displaystyle \lambda _{p} }}{\displaystyle {\displaystyle 4}}},$

(4.44)

где $p = I, II, III, \ldots$ .

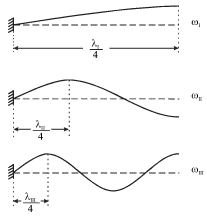
Соответствующие три низшие моды изображены на рис. 4.16. Очевидно, что это будут стоячие волны, отвечающие разным граничным условиям: на левом конце должен быть узел, а на правом - пучность. На длине шнура при этом укладывается нечетное число четвертей длин волн.

Рис. 4.16.

Замечание. При возбуждении моды мы задавали закон движения закрепленного конца шнура в виде $s(t) = \xi _{0} \sin \omega t,$ что может вызвать у читателя некоторое недоумение - как может двигаться закрепленный конец? Однако амплитуда колебаний $\xi _{0}$ обычно значительно меньше амплитуды колебаний в пучностях, поэтому незначительно вибрирующий конец шнура может рассматриваться, как неподвижный.

Волны в упругих телах.

Как мы видели, силы взаимодействия между соседними колеблющимися элементами шнура обеспечивают распространение в нем волн. В упругих телах такие силы сводятся к касательным и нормальным напряжениям, возникающим при деформациях сдвига и растяжения (сжатия). Этим деформациям соответствуют 2 типа волн: поперечные и продольные. Рассмотрим эти волны по отдельности.

Поперечные волны.

Если по стержню, изготовленному из упругого материала, ударить молотком в его средней части (рис. 4.17), то к его концам побегут импульсы, как это имело место в шнуре с грузами, изображенном на рис. 4.1. Однако поперечные смещения частиц стержня будут незаметны для глаза, поэтому для регистрации бегущих по стержню возмущений требуются специальные методы.

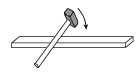Рис. 4.17.

Поскольку дисперсия волн механической природы в сплошной среде отсутствует, то скорость их распространения можно рассчитать с помощью волнового уравнения.

На рис. 4.18 показан фрагмент колеблющегося стержня. На средний элемент длиной $dx$ действуют касательные напряжения (слева $\sigma _{\tau } (x)$ и справа $\sigma _{\tau } (x + dx)$ ), величины которых пропорциональны деформациям сдвига соседних элементов:

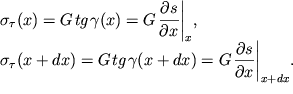$\begin{array}{l} \sigma _{\tau } (x) = G{\displaystyle \kern 1pt} tg{\displaystyle \kern 1pt} \gamma (x) = G{\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right|}_{x}, \\ \sigma _{\tau } (x + dx) = G{\displaystyle \kern 1pt} tg{\displaystyle \kern 1pt} \gamma (x + dx) = G{\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right|}_{x + dx}. \\ \end{array}$

(4.45)

Здесь $G$ - модуль сдвига, $\gamma$ - угол сдвига.

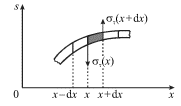Рис. 4.18.

Если площадь поперечного сечения стержня равна $S,$ то масса элемента $dm = S\rho dx$ ( $\rho$ - плотность материала). Следовательно, уравнение его движения может быть записано в виде:

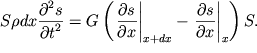$S\rho dx{\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial t^{2}}}} = G\left( {\displaystyle {\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right|}_{x + dx} - {\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right|}_{x} } \right)S.$

(4.46)

Поделив обе части (4.46) на $S$ и $dx,$ получаем волновое уравнение

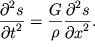${\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial t^{2}}}} = {\displaystyle \frac{\displaystyle {\displaystyle G}}{\displaystyle {\displaystyle \rho }}}{\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial x^{2}}}}.$

(4.47)

Его решением, как мы уже отмечали выше, является любая функция аргумента $\theta = t \mp x / c$ :

$s(x,t) = s(\theta ) = s\left( {\displaystyle t \mp {\displaystyle \frac{\displaystyle {\displaystyle x}}{\displaystyle {\displaystyle c}}}} \right),$

(4.48)

а скорость распространения волны

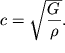$c = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle G}}{\displaystyle {\displaystyle \rho }}}}.$

(4.49)

Процессы распространения и отражения поперечных волн в стержне полностью аналогичны таковым в однородном натянутом шнуре, поэтому мы их рассматривать не будем. Сконцентрируем внимание на закономерностях переноса механической энергии бегущей волной.

Энергия, переносимая волной.

В лекции по деформациям упругих твердых тел мы отмечали, что при деформации сдвига в единице объема тела запасается потенциальная энергия

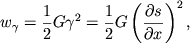$w_{\gamma } = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}G\gamma ^{2} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}G\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right)^{2},$

(4.50)

называемая объемной плотностью энергии деформации сдвига. В (4.50) полагаем $\gamma \approx tg\gamma = {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}.$

Помимо этого, единица объема с массой, равной $\rho,$ и колебательной скоростью $v = \partial s / \partial t$ имеет кинетическую энергию

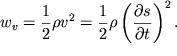$w_{v} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}\rho v^{2} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}\rho \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial t}}}} \right)^{2}.$

(4.51)

Полная энергия единицы объема равна

$w = w_{\gamma } + w_{v} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}{\displaystyle \left[ {\displaystyle G\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right)^{2} + \rho \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial t}}}} \right)^{2}} \right]}.$

(4.52)

Покажем, что в бегущей волне (4.48) $w_{\gamma } = w_{v}.$ Для этого вычислим производные:

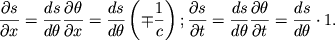${\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}} = {\displaystyle \frac{\displaystyle {\displaystyle ds}}{\displaystyle {\displaystyle d\theta }}}{\displaystyle \frac{\displaystyle {\displaystyle \partial \theta }}{\displaystyle {\displaystyle \partial x}}} = {\displaystyle \frac{\displaystyle {\displaystyle ds}}{\displaystyle {\displaystyle d\theta }}}\left( {\displaystyle \mp {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle c}}}} \right); {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial t}}} = {\displaystyle \frac{\displaystyle {\displaystyle ds}}{\displaystyle {\displaystyle d\theta }}}{\displaystyle \frac{\displaystyle {\displaystyle \partial \theta }}{\displaystyle {\displaystyle \partial t}}} = {\displaystyle \frac{\displaystyle {\displaystyle ds}}{\displaystyle {\displaystyle d\theta }}} \cdot 1.$

(4.53)

Из (4.53) получаем

${\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}} = \mp {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle c}}} \cdot {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial t}}},\; или \; \gamma = \mp {\displaystyle \frac{\displaystyle {\displaystyle v}}{\displaystyle {\displaystyle c}}}.$

(4.54)

Отметим, что в бегущей волне деформации $\gamma$ какого-либо элемента пропорциональны его колебательной скорости $v.$

Возводя в квадрат левое равенство (4.54), деля его пополам и учитывая, что $c^{2} = G / \rho,$ получаем

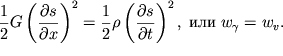${\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}G\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right)^{2} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}\rho \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial t}}}} \right)^{2}, \; или \; w_{\gamma } = w_{v}.$

(4.55)

Равенство величин $w_{\gamma }$ и $w_{v}$ позволяет записать полную плотность энергии w в виде:

$w = 2w_{\gamma } = 2w_{v}.$

(4.56)

Поскольку волна движется, то она осуществляет перенос механической энергии.

Так, например, за время $\Delta t$ через площадку единичной площади, заштрихованную на рис. 4.19, будет перенесена энергия, равная

$\Delta W = wc\Delta t.$

(4.57)

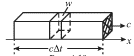Рис. 4.19.

Назад| Вперед