Астронет > Колебания и волны

Астронет: Научная Сеть/НС Колебания и волны
http://variable-stars.ru/db/msg/1175791/page18.html

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

Колебания систем со многими степенями свободы.

Основные идеи, сформулированные при рассмотрении колебаний систем с двумя степенями свободы, теперь могут быть с успехом использованы для анализа колебаний систем с тремя, четырьмя, $\ldots, N$ степенями свободы, и в пределе, при $N \to \infty ,$ для анализа колебаний в сплошных средах, т.е. волн.

Обратимся вначале к колебаниям трех одинаковых масс $m,$ закрепленных на равных расстояниях $а$ на натянутом легком резиновом шнуре, как показано на рис. 3.13а. Любое колебание этой системы может быть представлено как суперпозиция трех нормальных колебаний с частотами $\omega _{I} , \omega _{II}$ и $\omega _{III} .$ Опуская на время вопрос о величине частот, найдем конфигурацию этих мод. Примем во внимание, что квадрат частоты колебаний каждой массы в данной моде должен быть одинаков. Этого можно добиться в случае, когда отношения возвращающей силы к величине массы $m$ и ее смещению $s$ у всех грузов будут одинаковыми. Такие условия реализуются при смещении масс тремя способами (б, в и г на рис. 3.13). При отпускании грузов из положения (б) в системе будет происходить первое нормальное колебание на частоте $\omega _{I}$ ; из положения (в) - второе на частоте $\omega _{II}$ ; из положения (г) - третье на частоте $\omega _{III} .$ Очевидно, что $\omega _{III} \gt \omega _{II} \gt \omega _{I} .$

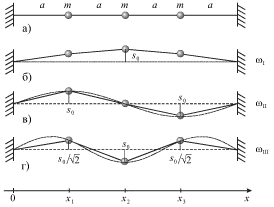Рис. 3.13.

Конфигурация каждой из мод может быть описана с помощью двух коэффициентов распределения амплитуд. Забегая вперед, отметим, что для четырех масс таких коэффициентов должно быть три, и т.д.

Однако ситуация может быть упрощена, если обратить внимание, что расположение масс в позициях (б), (в) и (г) на рис. 3.13 напоминает "синусоидальное" (пунктиром изображен фрагмент функции $\sin kx,$ где $k$ - некоторый параметр, характеризующий период этой функции). Тогда конфигурация первой моды будет описана следующим образом:

(3.44а)

$s_{0}^{I} (x) = s_{0} \sin k_{I} x; \quad k_{I} = {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle 4a}}}.$

Для второй моды:

(3.44б)

$s_{0}^{II} (x) = s_{0} \sin k_{II} x; \quad k_{II} = 2k_{I} .$

Для третьей моды:

(3.44в)

$s_{0}^{III} (x) = s_{0} \sin k_{III} x; \quad k_{III} = 3k_{I} .$

Роль безразмерных коэффициентов $\varsigma$ выполняет функция $\sin k_{p} x (p = I, II, III),$ вычисленная в точках $x = x_{1} = a, x = x_{2} = 2a, x = x_{3} = 3a.$

Другими примерами связанных осцилляторов являются атомы в молекулах CO₂, H₂O и т. д. На рис. 3.14 изображены конфигурации мод и приведены значения частот нормальных колебаний молекул. Обратим внимание, что эти частоты имеют порядок величины $(10^{13}\div 10^{14})$ с^-1 и значительно превышают (на несколько порядков) частоты механических колебаний макроскопических систем. Резонансные колебания этих (и других) молекул можно возбудить при взаимодействии разноименно заряженных ионов, составляющих эти молекулы, с электрическим полем световой электромагнитной волны инфракрасного (ИК) диапазона, имеющей близкую частоту.

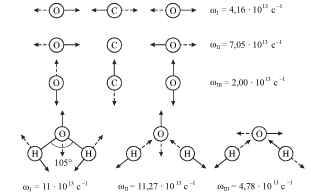Рис. 3.14.

В курсе "Оптика" мы познакомимся с таким взаимодействием, приводящим, в частности, к ослаблению (поглощению) энергии световой волны и ее рассеянию в среде с колеблющимися молекулами (комбинационному рассеянию).

Будем увеличивать число масс, закрепленных на шнуре через равные промежутки а. Если $N$ - число этих масс, то полная длина шнура равна $\ell = a(N + 1)$ (рис. 3.15). Рассчитаем нормальные частоты всех мод и их конфигурации. Будем считать, что невесомый шнур натянут с силой $F,$ и при малых отклонениях масс от положения равновесия $s \ll \ell$ эта сила не меняется. Каждая масса испытывает действие сил натяжения шнура по обе стороны от нее.

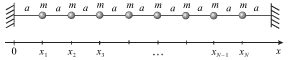Рис. 3.15.

На рис. 3.16 показано мгновенное положение фрагмента шнура и трех масс. Если углы $\theta _{1}$ и $\theta _{2}$ малы, то возвращающая сила, действующая на среднюю массу, равна:

(3.45)

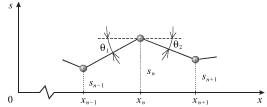$f = - F \cdot (\sin \theta _{1} + \sin \theta _{2} ) \approx - F(\theta _{1} + \theta _{2} ).$

Рис. 3.16.

Величины углов $\theta _{1}$ и $\theta _{2}$ определяются взаимным расположением масс:

(3.46)

$\theta _{1} \approx {\displaystyle \frac{\displaystyle {\displaystyle s_{n} - s_{n - 1} }}{\displaystyle {\displaystyle a}}}; \quad \theta _{2} \approx {\displaystyle \frac{\displaystyle {\displaystyle s_{n} - s_{n + 1} }}{\displaystyle {\displaystyle a}}}.$

С учетом (3.45) и (3.46) уравнение движения средней массы примет вид:

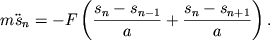(3.47)

$m\ddot {\displaystyle s}_{n} = - F\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle s_{n} - s_{n - 1} }}{\displaystyle {\displaystyle a}}} + {\displaystyle \frac{\displaystyle {\displaystyle s_{n} - s_{n + 1} }}{\displaystyle {\displaystyle a}}}} \right).$

Если колебания являются нормальными, то

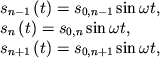(3.48)

$\begin{array}{l} s_{n - 1} \left( {\displaystyle t} \right) = s_{0,n - 1} \sin \omega t, \\ s_{n} \left( {\displaystyle t} \right) = s_{0,n} \sin \omega t, \\ s_{n + 1} \left( {\displaystyle t} \right) = s_{0,n + 1} \sin \omega t, \\ \end{array}$

где частоту $\omega$ и распределение амплитуд предстоит определить.

Подставляя (3.48) в (3.47), получим

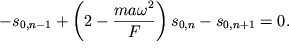(3.49)

$- s_{0,n - 1} + \left( {\displaystyle 2 - {\displaystyle \frac{\displaystyle {\displaystyle ma\omega ^{2}}}{\displaystyle {\displaystyle F}}}} \right)s_{0,n} - s_{0,n + 1} = 0.$

Поскольку $n = 1, 2, 3, \ldots, N,$ то (3.49) представляет собой систему $N$ линейных однородных уравнений. Из условия равенства нулю ее определителя можно рассчитать все $N$ нормальных частот, а затем для каждой из этих частот определить распределение амплитуд в каждой моде, число которых, очевидно, будет равно $N.$

Мы же используем уже описанный ранее более легкий путь и будем искать конфигурацию каждой моды в виде "синусоидальной" конфигурации:

(3.50)

$s_{0} (x) = s_{0} \sin kx,или \quad s_{0n} = s_{0} (x_{n} ),$

где $x_{1} = a, x_{2} = 2a,\ldots,x_{n} = na,\ldots,x_{N} = Na.$

Убедимся, что конфигурация (3.50) удовлетворяет уравнению (3.49), которое перепишем в виде:

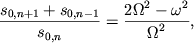(3.51)

${\displaystyle \frac{\displaystyle {\displaystyle s_{0,n + 1} + s_{0,n - 1} }}{\displaystyle {\displaystyle s_{0,n} }}} = {\displaystyle \frac{\displaystyle {\displaystyle 2\Omega ^{2} - \omega ^{2}}}{\displaystyle {\displaystyle \Omega ^{2}}}},$

где $\Omega ^{2} = {\displaystyle \frac{\displaystyle {\displaystyle F}}{\displaystyle {\displaystyle ma}}}.$

Подставим (3.50) в левую часть (3.51):

(3.52)

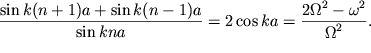${\displaystyle \frac{\displaystyle {\displaystyle \sin k(n + 1)a + \sin k(n - 1)a}}{\displaystyle {\displaystyle \sin kna}}} = 2\cos ka = {\displaystyle \frac{\displaystyle {\displaystyle 2\Omega ^{2} - \omega ^{2}}}{\displaystyle {\displaystyle \Omega ^{2}}}}.$

Очевидно, что (3.50) удовлетворит уравнению (3.49), если подобрать для данного $k$ подходящую частоту $\omega .$

Параметр $k$ назовем волновым числом. Объяснение этому будет дано в последующих лекциях. Этот параметр должен быть таким, чтобы на концах закрепленного шнура удовлетворялись граничные условия. При $x = 0$ эти условия выполняются: $\sin (k \cdot 0) = 0.$ На другом конце, где $x = a(N + 1),$ потребуем, чтобы

(3.53)

$\sin ka(N + 1) = 0,$

откуда получаем:

(3.54)

$k_{p} a(N + 1) = p \cdot \pi ,или \quad k_{p} = {\displaystyle \frac{\displaystyle {\displaystyle p\pi }}{\displaystyle {\displaystyle a(N + 1)}}},$

где целое число $p = I, II, \ldots, N$ характеризует номер моды (количество мод, как было показано выше, равно $N$ ). Каждой p-ой моде соответствует своя частота, которая легко находится из уравнения (3.52):

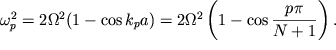(3.55)

$\omega _{p}^{2} = 2\Omega ^{2}(1 - \cos k_{p} a) = 2\Omega ^{2}\left( {\displaystyle 1 - \cos {\displaystyle \frac{\displaystyle {\displaystyle p\pi }}{\displaystyle {\displaystyle N + 1}}}} \right).$

Зная волновые числа $k_{p}$ и нормальные частоты $\omega _{p} ,$ не составляет труда записать выражения для смещений всех масс, как функций времени. Для р-ой моды можно записать:

(3.56)

$s_{p} (x_{n} ,t) = s_{0p} \sin k_{p} x_{n} \cdot \sin (\omega _{p} t + \varphi _{p} );$

здесь $x_{n} = na; n = 1, 2, \ldots, N.$

Амплитуда $s_{0p}$ и начальная фаза $\varphi _{p}$ определяются начальными условиями, а $k_{p}$ и $\omega _{p}$ - свойствами самой системы (формулы 3.54 и 3.55).

В силу линейности колебательной системы в самом общем случае колебаний получаем для смещения всех частиц выражение:

(3.57)

$s(x_{n} ,t) = {\displaystyle \sum\limits_{p} {\displaystyle s_{p} \left( {\displaystyle x_{n} ,t} \right),} }$

где суммирование проводится только по тем модам, которые "участвуют" в колебаниях.

Так, например, удерживая все время среднюю массу в положении равновесия, мы не можем возбудить моды с нечетными номерами $p = I, III, \ldots,$ поскольку эти моды "требуют" смещения центральной массы.

Пользуясь формулой (3.55), нетрудно вычислить нормальные частоты колеблющихся масс на шнуре.

На рис. 3.17 изображены моды колебаний в системе с одной, двумя и тремя массами и для каждой моды указаны величины нормальных частот.

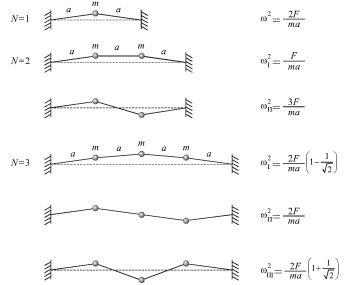Рис. 3.17.

В заключение отметим, что связь типа (3.55) между частотой $\omega$ и волновым числом $k$ называется дисперсионным соотношением. Это соотношение будет далее использовано при анализе распространения волн в периодических структурах.

Назад| Вперед