Астронет > Колебания и волны

Астронет: Научная Сеть/НС Колебания и волны
http://variable-stars.ru/db/msg/1175791/page16.html

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

Методика анализа колебаний связанных осцилляторов.

Выше мы рассмотрели колебания двух одинаковых связанных пружинных маятников, не прибегая к решению уравнений их движения. Однако, если жесткости пружин и массы тел имеют произвольные величины, то зачастую бывает трудно догадаться о конфигурации мод и их частотах. Поэтому представляется важным вооружиться универсальным методом, позволяющим по единой схеме провести последовательный анализ любой колебательной системы с двумя степенями свободы, являющейся системой любых связанных осцилляторов.

Запишем уравнения движения двух связанных пружинных маятников в виде:

(3.20)

$\begin{array}{l} m_{1} \ddot {\displaystyle s}_{1} = - k_{1} s_{1} - {\displaystyle k}'s_{1} + {\displaystyle k}'s_{2} ; \\ m_{2} \ddot {\displaystyle s}_{2} = - k_{2} s_{2} - {\displaystyle k}'s_{2} + {\displaystyle k}'s_{1} . \\ \end{array}$

Разделив первое уравнение на $m_{1} ,$ а второе - на $m_{2}$ и используя выражения (3.6) для парциальных частот, перепишем (3.20) следующим образом:

(3.21)

$\begin{array}{l} \ddot {\displaystyle s}_{1} = - \omega _{1}^{2} s_{1} - \alpha _{1} s_{2} , \\ \ddot {\displaystyle s}_{2} = - \alpha _{2} s_{1} - \omega _{2}^{2} s_{2} , \\ \end{array}$

где $\alpha _{1} = - {\displaystyle k}' / m_{1} , \alpha _{2} = - {\displaystyle k}' / m_{2}$ - коэффициенты, зависящие от жесткости ${\displaystyle k}'$ пружины связи. Обратим внимание, что уравнения (3.21) не могут решаться по отдельности, т.к. каждое из них содержит $s_{1}$ и $s_{2} .$ Поэтому целесообразно перейти от смещений $s_{1}$ и $s_{2}$ к новым функциям $\xi _{1}$ и $\xi _{2} ,$ называемым нормальными координатами. Смысл перехода состоит в получении двух независимых уравнений движения, которые можно решать по отдельности.

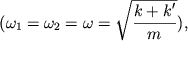Однако, в общем случае эти координаты найти не просто. 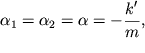Поэтому для иллюстрации такого перехода рассмотрим систему с одинаковыми массами $(m_{1} = m_{2} = m)$ и пружинами $(k_{1} = k_{2} = k).$ Поскольку парциальные частоты совпадают $(\omega _{1} = \omega _{2} = \omega = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k + {\displaystyle k}'}}{\displaystyle {\displaystyle m}}}} ),$ а также $\alpha _{1} = \alpha _{2} = \alpha = - {\displaystyle \frac{\displaystyle {\displaystyle {\displaystyle k}'}}{\displaystyle {\displaystyle m}}},$ то система уравнений (3.21) становится более простой. Сложив оба уравнения, получаем:

(3.22а)

$\ddot {\displaystyle \xi }_{1} = - (\omega ^{2} + \alpha )\xi _{1} ,$

где $\xi _{1} = s_{1} + s_{2}$ - первая нормальная координата. Вычитая второе уравнение из первого, находим:

(3.22б)

$\ddot {\displaystyle \xi }_{2} = - (\omega ^{2} - \alpha )\xi _{2} ,$

где $\xi _{2} = s_{1} - s_{2}$ - вторая нормальная координата. Теперь уравнения (3.22) независимы. Первое из них описывает колебание центра масс системы с частотой

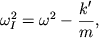(3.23)

$\omega _{I}^{2} = \omega ^{2} - {\displaystyle \frac{\displaystyle {\displaystyle {\displaystyle k}'}}{\displaystyle {\displaystyle m}}},$

меньшей парциальной частоты $\omega .$ Второе уравнение описывает изменение расстояния между двумя массами с частотой

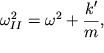(3.24)

$\omega _{II}^{2} = \omega ^{2} + {\displaystyle \frac{\displaystyle {\displaystyle {\displaystyle k}'}}{\displaystyle {\displaystyle m}}},$

превышающей парциальную частоту. Решения уравнений (3.22) очевидны:

(3.25а)

$\xi _{1} (t) = s_{1} (t) + s_{2} (t) = \xi _{01} \sin (\omega _{I} t + \varphi _{I} );$

(3.25б)

$\xi _{2} (t) = s_{1} (t) - s_{2} (t) = \xi _{02} \sin (\omega _{II} t + \varphi _{II} ).$

Возвращаясь к функциям $s_{1}$ и $s_{2} ,$ получаем:

(3.26а)

$s_{1} (t) = {\displaystyle \frac{\displaystyle {\displaystyle \xi _{01} }}{\displaystyle {\displaystyle 2}}}\sin (\omega _{I} t + \varphi _{I} ) + {\displaystyle \frac{\displaystyle {\displaystyle \xi _{02} }}{\displaystyle {\displaystyle 2}}}\sin (\omega _{II} t + \varphi _{II} );$

(3.26б)

$s_{2} (t) = {\displaystyle \frac{\displaystyle {\displaystyle \xi _{01} }}{\displaystyle {\displaystyle 2}}}\sin (\omega _{I} t + \varphi _{I} ) - {\displaystyle \frac{\displaystyle {\displaystyle \xi _{02} }}{\displaystyle {\displaystyle 2}}}\sin (\omega _{II} t + \varphi _{II} ).$

Четыре величины $\xi _{01} , \xi _{02} , \varphi _{I} и \varphi _{II}$ определяются из начальных условий: $s_{1} (t = 0), s_{2} (t = 0), \dot {\displaystyle s}_{1} (t = 0), \dot {\displaystyle s}_{2} (t = 0).$

Проиллюстрировав переход к нормальным координатам, вернемся к методике анализа колебаний в произвольных системах, описываемых уравнениями (3.21).

Пусть в системе происходит нормальное колебание с неизвестной пока частотой $\omega$ и коэффициентом распределения амплитуд $\varsigma = {\displaystyle \frac{\displaystyle {\displaystyle s_{02} }}{\displaystyle {\displaystyle s_{01} }}}$ :

(3.27)

$s_{1} (t) = s_{01} \sin (\omega t + \varphi ), \quad s_{2} (t) = s_{02} \sin (\omega t + \varphi ).$

Подставим (3.27) в систему уравнений (3.21). Тогда получим систему из двух алгебраических уравнений:

(3.28)

$\begin{array}{l} (\omega _{1}^{2} - \omega ^{2})s_{01} + \alpha _{1} s_{02} = 0; \\ \alpha _{2} s_{01} + (\omega _{2}^{2} - \omega ^{2})s_{02} = 0. \\ \end{array}$

Система линейных однородных уравнений (3.28) имеет отличные от нуля решения только в том случае, если ее определитель равен нулю:

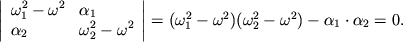(3.29)

${\displaystyle \left| {\displaystyle {\displaystyle \begin{array}{ *{20}c} {\displaystyle \omega _{1}^{2} - \omega ^{2}} \hfill & {\displaystyle \alpha _{1} } \hfill \\ {\displaystyle \alpha _{2} } \hfill & {\displaystyle \omega _{2}^{2} - \omega ^{2}} \hfill \\ \end{array} }} \right|} = (\omega _{1}^{2} - \omega ^{2})(\omega _{2}^{2} - \omega ^{2}) - \alpha _{1} \cdot \alpha _{2} = 0.$

Это - квадратное уравнение относительно $\omega ^{2},$ причем $\omega \gt 0.$ Поэтому, решая уравнение (3.29), можно найти нормальные частоты $\omega _{I}$ и $\omega _{II} .$ После нахождения частот не составляет труда найти конфигурацию мод, т.е. коэффициенты распределения амплитуд $\varsigma _{I}$ и $\varsigma _{II} .$ Их можно определить, например, из первого уравнения (3.28), причем очевидно, что для каждой нормальной частоты ( $\omega _{I}$ или $\omega _{II}$ ) эти коэффициенты различны:

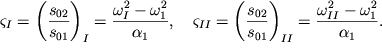(3.30)

$\varsigma _{I} = \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle s_{02} }}{\displaystyle {\displaystyle s_{01} }}}} \right)_{I} = {\displaystyle \frac{\displaystyle {\displaystyle \omega _{I}^{2} - \omega _{1}^{2} }}{\displaystyle {\displaystyle \alpha _{1} }}}, \quad \varsigma _{II} = \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle s_{02} }}{\displaystyle {\displaystyle s_{01} }}}} \right)_{II} = {\displaystyle \frac{\displaystyle {\displaystyle \omega _{II}^{2} - \omega _{1}^{2} }}{\displaystyle {\displaystyle \alpha _{1} }}}.$

Таким образом, уравнение (3.29) и равенство (3.30) позволяют полностью рассчитать параметры каждой из двух мод. Движение каждой из масс, как уже неоднократно отмечалось, является суперпозицией двух нормальных колебаний:

$s_{1} (t) = s_{01_{I} } \sin (\omega _{I} t + \varphi _{I} ) + s_{01_{II} } \sin (\omega _{II} t + \varphi _{II} ),$

$s_{2} (t) = \varsigma _{I} \cdot s_{01_{I} } \sin (\omega _{I} t + \varphi _{I} ) + \varsigma _{II} \cdot s_{01_{II} } \sin (\omega _{II} t + \varphi _{II} ),$

где амплитуды $s_{01_{I} }$ и $s_{01_{II} }$ и начальные фазы $\varphi _{I}$ и $\varphi _{II}$ определяются, как и раньше, из начальных условий: $s_{1} (0), s_{2} (0), \dot {\displaystyle s}_{1} (0), \dot {\displaystyle s}_{2} (0).$

Расчет мод для любой системы двух связанных осцилляторов читатель может проделать самостоятельно.

Соотношение между парциальными и нормальными частотами.

Для установления связи между парциальными и нормальными частотами перепишем (3.29) в виде

(3.31)

$(\omega _{1}^{2} - \omega ^{2})(\omega _{2}^{2} - \omega ^{2}) - \gamma ^{2}\omega _{1}^{2} \omega _{2}^{2} = 0,$

где

(3.32)

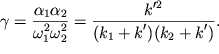$\gamma = {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{1} \alpha _{2} }}{\displaystyle {\displaystyle \omega _{1}^{2} \omega _{2}^{2} }}} = {\displaystyle \frac{\displaystyle {\displaystyle {\displaystyle k}'^{2}}}{\displaystyle {\displaystyle (k_{1} + {\displaystyle k}')(k_{2} + {\displaystyle k}')}}}.$

Безразмерный коэффициент связи \gamma между двумя системами может принимать значения $0 \lt \gamma \lt 1.$ Если из (3.31) определить нормальные частоты $\omega _{I}$ и $\omega _{II} ,$ то они будут выражаться через парциальные частоты $\omega _{1}$ и $\omega _{2}$ и коэффициент $\gamma .$ Эти четыре частоты будут располагаться на оси частот в последовательности, изображенной на рис. 3.9.

Рис. 3.9.

При слабой связи $(\gamma \ll 1)$ нормальные частоты близки к парциальным, а при сильной связи $(\gamma \leq 1)$ различие в частотах становится существенным. Это хорошо видно, если парциальные частоты совпадают $\left( {\displaystyle \omega _{1} = \omega _{2} = \omega _{0} } \right).$ Тогда (3.31) примет вид:

$(\omega _{0}^{2} - \omega ^{2})^{2} - \gamma ^{2}\omega _{0}^{4} = 0.$

Отсюда

(3.33)

$\omega _{I}^{2} = \omega _{0}^{2} \left( {\displaystyle 1 - \gamma } \right), \quad \omega _{II}^{2} = \omega _{0}^{2} \left( {\displaystyle 1 + \gamma } \right).$

Назад| Вперед