Astronet Астронет:  Научная Сеть/НС Колебания и волны
http://variable-stars.ru/db/msg/1175791/page12.html

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

Параметрические колебания.

В повседневной жизни мы сталкиваемся с незатухающими колебаниями, для поддержания которых требуется периодически менять какой-либо параметр колебательной системы. Одним из ярких примеров являются колебания качелей. Хорошо известно, что можно поддерживать колебания длительное время, если быстро приседать в момент наибольшего отклонения качелей и также быстро вставать при прохождении положения равновесия. Благодаря этому параметр физического маятника (качелей) - расстояние $a$ между осью вращения и центром масс - меняется скачкообразно на величину $\pm \Delta a (\Delta a \ll a)$.Величина $\Delta a$ должна быть такой, чтобы обеспечить баланс энергии системы: потери энергии маятника за период должны компенсироваться за счет совершения работы, осуществляемой при приседании и вставании.

Напишем условие энергетического баланса для простейшего случая колебаний математического маятника с длиной нити a, которая меняется на величину $\pm \Delta a$ (рис. 2.8.). Это можно осуществить, если пропустить нить маятника через отверстие в точке P (точке подвеса) и затем, прикладывая внешнюю силу ${\displaystyle \bf F}$ к концу нити, периодически менять ее длину.

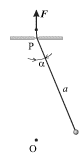Рис.2.8.

Рассмотрим установившиеся параметрические колебания маятника с не слишком большими амплитудами и будем считать, что затухание мало $(\delta \ll \omega _{0} ).$ Поскольку $\Delta a \ll a,$ то приближенно можно считать, что угол $\alpha$ отклонения маятника от положения равновесия меняется во времени по гармоническому закону

$ \alpha (t) = \alpha _{0} \sin \omega t, $(2.53)

где согласно (1.42) 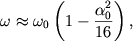$\omega \approx \omega _{0} \left( {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 16}}}} \right),$ а $\omega _{0} = \sqrt {\displaystyle {\displaystyle {\displaystyle g} / {\displaystyle a}}.}$

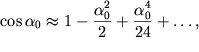В момент наибольшего отклонения на угол $\alpha _{0}$ сила натяжения нити равна $N_{1} = mg\cos \alpha _{0} .$ Поэтому, удлиняя нить на величину $\Delta a,$ внешняя сила $F_{1} = N_{1}$ совершает отрицательную работу $A_{ - } = - mg\cos \alpha _{0} \cdot \Delta a.$ Раскладывая $\cos \alpha _{0}$ в ряд $\cos \alpha _{0} \approx 1 - {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 2}}} + {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{4} }}{\displaystyle {\displaystyle 24}}} + \ldots,$ получим

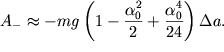$ A_{ - } \approx - mg\left( {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 2}}} + {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{4} }}{\displaystyle {\displaystyle 24}}}} \right)\Delta a. $(2.54)

При прохождении маятником положения равновесия 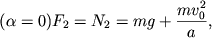$(\alpha = 0) F_{2} = N_{2} = mg + {\displaystyle \frac{\displaystyle {\displaystyle mv_{0}^{2} }}{\displaystyle {\displaystyle a}}},$ где $v_{0} = \alpha _{0} \omega a.$ Поэтому положительная работа при укорачивании нити с точностью до членов порядка $\alpha _{0}^{4}$ равна:

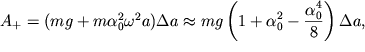$ A_{ + } = (mg + m\alpha _{0}^{2} \omega ^{2}a)\Delta a \approx mg\left( {\displaystyle 1 + \alpha _{0}^{2} - {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{4} }}{\displaystyle {\displaystyle 8}}}} \right)\Delta a, $(2.55)

где учтено, что $\omega _{0}^{2} a = g.$

Полная работа, совершаемая за период внешней силой ${\displaystyle \bf F},$ будет положительной и равной

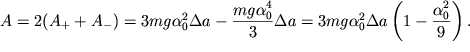$ A = 2(A_{ + } + A_{ - } ) = 3mg\alpha _{0}^{2} \Delta a - {\displaystyle \frac{\displaystyle {\displaystyle mg\alpha _{0}^{4} }}{\displaystyle {\displaystyle 3}}}\Delta a = 3mg\alpha _{0}^{2} \Delta a\left( {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 9}}}} \right). $(2.56)

Потери энергии за период численно равны работе силы трения:

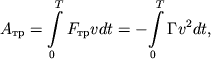$ A_{тр} = {\displaystyle \int\limits_{0}^{T} {\displaystyle F_{тр} vdt = - {\displaystyle \int\limits_{0}^{T} {\displaystyle \Gamma v^{2}dt,} }} } $(2.57)

где $F_{тр} = - \Gamma v.$

При гармонических колебаниях (2.53) скорость

$ v(t) = a\dot {\displaystyle \alpha }(t) = a\alpha _{0} \omega \cos \omega t. $(2.58)

Подставляя (2.58) в (2.57) и выполняя интегрирование, получаем:

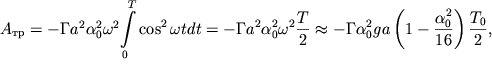$ A_{тр} = - \Gamma a^{2}\alpha _{0}^{2} \omega ^{2}{\displaystyle \int\limits_{0}^{T} {\displaystyle \cos ^{2}\omega tdt = - \Gamma a^{2}\alpha _{0}^{2} \omega ^{2}{\displaystyle \frac{\displaystyle {\displaystyle T}}{\displaystyle {\displaystyle 2}}} \approx - \Gamma \alpha _{0}^{2} ga\left( {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 16}}}} \right){\displaystyle \frac{\displaystyle {\displaystyle T_{0} }}{\displaystyle {\displaystyle 2}}}} }, $(2.59)

поскольку $\omega T = \omega _{0} T_{0} = 2\pi .$

Следовательно, условие баланса энергии состоит в равенстве нулю суммы работ: $A + A_{тр} = 0,$ или

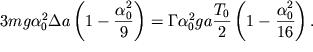$ 3mg\alpha _{0}^{2} \Delta a\left( {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 9}}}} \right) = \Gamma \alpha _{0}^{2} ga{\displaystyle \frac{\displaystyle {\displaystyle T_{0} }}{\displaystyle {\displaystyle 2}}}\left( {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 16}}}} \right). $(2.60)

Проводя сокращения и используя определение выражение для добротности $Q \approx {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle \delta T_{0} }}},$ получаем приближенное выражение для амплитуды $\alpha _{0}$ установившихся параметрических колебаний:

$ \alpha _{0} = {\displaystyle \frac{\displaystyle {\displaystyle 12}}{\displaystyle {\displaystyle \sqrt {\displaystyle 7} }}}\sqrt {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle 3Q(\Delta {\displaystyle {\displaystyle a} / {\displaystyle a}})}}}} . $(2.61)

Отношение $\Delta a / a$ называют глубиной модуляции параметра $a.$ Из (2.61) видно, что для возникновения параметрических колебаний глубина модуляции должна превзойти некоторое минимальное (пороговое) значение, примерно равное величине, обратной добротности:

$ {\displaystyle \frac{\displaystyle {\displaystyle \Delta a}}{\displaystyle {\displaystyle a}}} \geq {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle Q}}}. $(2.62)

Чем более добротна система, тем меньше пороговая глубина модуляции. С повышением величины $\Delta a / a$ амплитуда колебаний $\alpha _{0} ,$ как это следует из формулы (2.61), будет увеличиваться. Однако при больших амплитудах $(\alpha _{0} \gt 1)$ формула (2.61) становится мало приемлемой, поскольку сделанные нами приближения становятся неприменимыми.

Следует отметить, что параметрическое возбуждение является существенно нелинейным эффектом. Это видно, в частности, из уравнения (2.60): если пренебречь в нем малыми слагаемыми $\sim \alpha _{0}^{2} ,$ которые описывают нелинейность, то $\alpha _{0}$ из уравнения выпадает, и получается соотношение ${\displaystyle \frac{\displaystyle {\displaystyle \Delta a}}{\displaystyle {\displaystyle a}}} = {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle 3Q}}}.$ Физически это означает, что при этом значении глубины модуляции энергетический баланс в системе обеспечивается при любых амплитудах $\alpha _{0} ,$ что неверно.

Заметим, что возбуждение параметрических колебаний, вообще говоря, может происходить не только на удвоенной частоте собственных колебаний системы, когда параметр меняется один раз за каждые полпериода, но и при более редком воздействии: через один, два, три и т. д. полпериодов колебаний, т.е. на частотах $2\omega _{0} / n,$ где $n$ - любое целое число. Возбуждение также возможно внутри некоторой области - вблизи каждой из этих частот, но пороговые значения глубины модуляции для разных частот будут различны.

Автоколебания.

Наблюдая колебания листьев деревьев, дорожных знаков над проезжей частью улиц, полотнищ на ветру и др., мы понимаем, что во всех перечисленных случаях незатухающие колебания происходят за счет энергии постоянно дующего ветра. При этом сама колебательная система производит отбор энергии ветра в нужный момент времени и в количестве, требуемом для компенсации неизбежно присутствующих энергетических потерь. Колебания в этих системах начинаются самопроизвольно за счет начальных флуктуаций (дрожаний) колеблющихся предметов. Частота и амплитуда установившихся колебаний определяется как параметрами самой системы, так и параметрами ее взаимодействия с ветром. Такие колебания являются примерами автоколебаний, а сами системы - примерами автоколебательных систем.

Классическим примером автоколебательной системы служат механические часы с маятником и гирями. Эти часы периодически "черпают" энергию при опускании гирь, подвешенных к цепочке, перекинутой через шестерню часового механизма.

Принцип работы всех автоколебательных систем можно понять, обратившись к схеме, изображенной на рис. 2.9а.

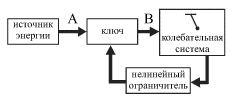Рис. 2.9а.

Периодическим поступлением энергии в колебательную систему от источника энергии по каналу АВ управляет сама колебательная система посредством обратной связи. Схематически это изображено в виде некоторого запирающего канал АВ устройства (ключа), который управляется самой системой. Так, в зависимости от положения и скорости колеблющегося листа на ветру будет различной мощность сил аэродинамического давления. В конструкции часового механизма (рис. 2.9б) присутствует специальное устройство - анкер, выполняющий роль ключа. Этот анкер, представляющий собой коромысло, приводится в колебание самим маятником часов. При определенных положениях он "отпирает" одну из шестерен часового механизма. В этот момент времени шестерня проворачивается за счет момента сил, приложенного со стороны натянутой цепи с грузом. Груз при этом опускается на небольшую величину. Количество энергии, поступающей в часовой механизм, равно по величине уменьшению потенциальной энергии груза в поле силы тяжести.

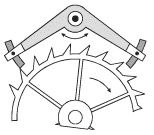Рис. 2.9б.

Важно отметить, что любая автоколебательная система нелинейна. На схеме это отражено наличием в системе обратной связи нелинейного ограничителя сигнала, управляющего ключом. Нелинейность системы проявляется в том, что при начальном нарастании амплитуды колебаний, порожденных флуктуациями, поступление энергии в систему за каждый последующий период колебаний увеличивается нелинейно, т.е. прирост поступающей энергии становится все меньше и меньше. Естественно, что амплитуда колебаний достигнет такой установившейся величины, при которой приток энергии и ее потери будут равны по величине.

Назад| Вперед

Rambler's Top100 Яндекс цитирования