Астронет > Механика твердого тела. Лекции.

Астронет: Физический факультет МГУ Механика твердого тела. Лекции.
http://variable-stars.ru/db/msg/1175788/page8.html

Механика твердого тела. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 1997 г. Содержание

Вычисление моментов инерции относительно оси.

Прямой расчет момента инерции тела относительно оси сводится к вычислению интеграла

$J = \int {\displaystyle \rho ^{2}} \cdot dm,$

(2.44)

где $\rho$ - расстояние элементарной массы $dm$ до оси вращения. При этом, естественно, необходимо учитывать симметрию системы.

Вычислим, к примеру, момент инерции шара (в сферических координатах $r, \theta , \varphi ,$ рис. 2.15) относительно произвольной оси, проходящей через его центр (в данном случае относительно оси Oz):

$dm = {\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle V}}} \cdot dV = {\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle V}}}r^{2}\sin \theta \cdot dr \cdot d\theta \cdot d\varphi ;$

(2.45)

$m$ - масса шара, $V$ - его объем.

$\rho = r\sin \theta ,$

(2.46)

поэтому

$dJ = \rho ^{2} \cdot dm = {\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle V}}}r^{4}\sin ^{3}\theta \cdot dr \cdot d\theta \cdot d\varphi ;$

(2.47)

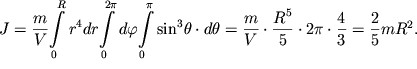$J = {\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle V}}}{\displaystyle \int\limits_{0}^{R} {\displaystyle r^{4}} }dr{\displaystyle \int\limits_{0}^{2\pi } {\displaystyle d\varphi } }{\displaystyle \int\limits_{0}^{\pi } {\displaystyle \sin ^{3}} }\theta \cdot d\theta = {\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle V}}} \cdot {\displaystyle \frac{\displaystyle {\displaystyle R^{5}}}{\displaystyle {\displaystyle 5}}} \cdot 2\pi \cdot {\displaystyle \frac{\displaystyle {\displaystyle 4}}{\displaystyle {\displaystyle 3}}} = {\displaystyle \frac{\displaystyle {\displaystyle 2}}{\displaystyle {\displaystyle 5}}}mR^{2}.$

(2.48)

Рис. 2.15.

Если считать, что наша Земля - шар с постоянной плотностью массы, то момент инерции Земли относительно центральной оси будет равен

$J_{Земли} = 0,4 M_{З} R_{З}^{2} = 0,4 \cdot 0,6 \cdot 10^{24} кг \cdot \left( {\displaystyle 6,4 \cdot 10^{6} м} \right)^{2} \approx 10^{38} кг \cdot м^{2}.$

Для сравнения рассчитаем момент инерции молекулы CO₂ относительно оси, проходящей через атом углерода перпендикулярно линии, вдоль которой расположены все три атома (рис. 2.16).

Рис. 2.16.

Основная масса атомов сосредоточена в их ядрах; размеры ядер (~10^-14 м) значительно меньше межядерного расстояния (~10^-10 м), поэтому атомы кислорода можно считать материальными точками, а моментом инерции атома углерода можно пренебречь. При этих условиях $J_{CO_{2} } = 2{\displaystyle \frac{\displaystyle {\displaystyle \mu _{O_{2} } }}{\displaystyle {\displaystyle 2N_{A} }}} \cdot \ell ^{2},$ где $\mu _{O_{2} }$ - молярная масса кислорода, $N_{A}$ - число Авогадро, $\ell$ - межядерное расстояние (см. рис. 2.16). Подставляя числовые значения этих величин, получим

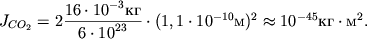$J_{CO_{2} } = 2{\displaystyle \frac{\displaystyle {\displaystyle 16 \cdot 10^{ - 3} кг}}{\displaystyle {\displaystyle 6 \cdot 10^{23}}}} \cdot (1,1 \cdot 10^{ - 10} м)^{2} \approx 10^{ - 45} кг \cdot м^{2}.$

Для плоской фигуры моменты инерции относительно трех взаимно перпендикулярных осей, две из которых лежат в плоскости фигуры, оказываются связанными между собой простым соотношением. Из рис. 2.17 следует, что

$dJ_{z} = \rho ^{2} \cdot dm = \left( {\displaystyle x^{2} + y^{2}} \right)dm = dJ_{y} + dJ_{x} ,$

(2.49)

откуда

$J_{z} = J_{x} + J_{y}$

(2.50)

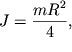Это соотношение позволяет, например, легко вычислить момент инерции тонкого диска массы $m$ и радиуса $R$ относительно оси, проходящей через центр диска и лежащей в его плоскости (любая такая ось будет главной): $J = {\displaystyle \frac{\displaystyle {\displaystyle mR^{2}}}{\displaystyle {\displaystyle 4}}},$ поскольку момент инерции диска относительно главной центральной оси, перпендикулярной плоскости диска, $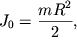J_{0} = {\displaystyle \frac{\displaystyle {\displaystyle mR^{2}}}{\displaystyle {\displaystyle 2}}},$ а $J_{0} = 2J.$

Рис. 2.17.

Теорема Гюйгецса-Штейнера.

Эта теорема связывает моменты инерции относительно двух параллельных осей, одна из которых проходит через центр масс тела.

Ось 1 на рис. 2.18 проходит через центр масс О, ось 2 параллельна ей; расстояние между осями равно $a.$ $\bf R}_{i$ и $\rho_{i}$ - векторы, перпендикулярные осям 1 и 2. Они проведены от осей в ту точку, где расположена масса $\Delta m_{i} .$

Рис. 2.18.

Момент инерции тела относительно оси 2

$J = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }\rho _{i}^{2} = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }\left( {\displaystyle {\displaystyle \bf R}_{i} - {\displaystyle \bf a}} \right)^{2} = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }R_{i}^{2} + {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }a^{2} - 2{\displaystyle \bf a}{\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }{\displaystyle \bf R}_{i} .$

(2.51)

Последняя сумма равна нулю, поскольку ось 1 проходит через центр масс, и

$J = J_{0} + ma^{2}.$

(2.52)

Если, например, ось - касательная к поверхности шара, то можно, не проводя громоздких вычисление, записать:

$J = J_{0} + mR^{2} = {\displaystyle \frac{\displaystyle {\displaystyle 2}}{\displaystyle {\displaystyle 5}}}mR^{2} + mR^{2} = {\displaystyle \frac{\displaystyle {\displaystyle 7}}{\displaystyle {\displaystyle 5}}}mR^{2}.$

(2.53)

Момент импульса тела относительно движущегося центра масс.

До сих пор, рассматривая момент импульса твердого тела, мы определяли его относительно некоторой неподвижной в лабораторной системе XYZ точки (например, точки закрепления тела). Во многих задачах динамики это оказывается неудобно. Например, решая задачу о диске, скатывающемся с наклонной плоскости, логично рассматривать момент импульса диска относительно его центра масс, а не относительно точки, принадлежащей наклонной плоскости.

Рассмотрим, как будут связаны моменты импульса тела, определенные относительно некоторой неподвижной точки О' и относительно центра масс тела О, движущегося произвольным образом (рис. 2.19).

Рис. 2.19.

Пусть ${\displaystyle \bf r}}'_{i$ и $\bf }r_{i$ - радиусы-векторы элементарной массы $\Delta m_{i}$ - тела относительно точек O' и O, R - радиус-вектор, проведенный из O' в O. Эти векторы связаны между собой очевидным соотношением

${\displaystyle \bf r}}'_{i} = {\displaystyle \bf R} + {\displaystyle \bf r}_{i$

(2.54)

Момент импульса тела относительно точки O' (см. формулу (2.1))

${\displaystyle \bf L}_{O'} = {\displaystyle \sum\limits_{i} {\displaystyle {\displaystyle {\displaystyle \bf r}}'_{i} } }\times \Delta m_{i} {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle {\displaystyle \bf r}}'_{i} }}{\displaystyle {\displaystyle dt}}} = {\displaystyle \sum\limits_{i} {\displaystyle {\displaystyle \left[ {\displaystyle \left( {\displaystyle {\displaystyle \bf R} + {\displaystyle \bf r}_{i} } \right)\times \Delta m_{i} \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf R}}}{\displaystyle {\displaystyle dt}}} + {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf r}_{i} }}{\displaystyle {\displaystyle dt}}}} \right)} \right]}} }.$

(2.55)

Воспользуемся очевидными равенствами

${\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } } = M$

(2.56)

( $М$ - масса всего тела);

${\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }{\displaystyle \bf r}_{i} = 0$

(2.57)

${\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }{\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf r}_{i} }}{\displaystyle {\displaystyle dt}}} = 0,$

(2.58)

поскольку точка О совпадает с центром масс тела. С учетом (2.56 - 2.58) из (2.55) получим

${\displaystyle \bf L}_{O'} = {\displaystyle \bf R}\times M{\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf R}}}{\displaystyle {\displaystyle dt}}} + {\displaystyle \sum\limits_{i} {\displaystyle {\displaystyle \bf r}_{i} } }\times \Delta m_{i} {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf r}_{i} }}{\displaystyle {\displaystyle dt}}} = {\displaystyle \bf R}\times {\displaystyle \bf p} + {\displaystyle \sum\limits_{i} {\displaystyle {\displaystyle \bf r}_{i} } }\times \Delta m_{i} {\displaystyle \bf v}_{i} ,$

(2.59)

где $\bf p} = M{\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf R}}}{\displaystyle {\displaystyle dt}}$ - полный импульс тела в лабораторной системе XYZ, $\bf v}_{i$ - скорость i-ой массы относительно центра масс.

Если момент импульса тела относительно его центра масс (относительный момент импульса) определить как

${\displaystyle \bf L}_{O} = {\displaystyle \sum\limits_{i} {\displaystyle {\displaystyle \bf r}_{i} } }\times \Delta m_{i} {\displaystyle \bf v}_{i} ,$

(2.60)

то из (2.59) следует искомое соотношение

${\displaystyle \bf L}_{O'} = {\displaystyle \bf L}_{O} + {\displaystyle \bf R}\times {\displaystyle \bf p}.$

(2.61)

Еще раз подчеркнем, что при определении момента импульса тела относительно его центра масс (величина ${\displaystyle \bf L}_O$ (следует брать относительные скорости всех точек тела, то есть скорости точек тела относительно центра масс, считая его как бы неподвижным.

Замечание. Соотношение (2.61) позволяет также связать моменты импульса относительно двух параллельных осей, одна из которых неподвижна, а другая проходит через центр масс движущегося тела.

Обратимся к примерам.

1. Момент импульса цилиндра, скатывающегося без проскальзывания с наклонной плоскости, относительно его оси равен $J_{0} \omega$ ( $J_{0}$ - момент инерции цилиндра относительно его оси, $\omega$ - мгновенная угловая скорость вращения цилиндра). Момент импульса того же цилиндра относительно мгновенной оси вращения, проходящей через точку касания цилиндра и плоскости, будет равен $J_{0} \omega + Rmv_{0} = J_{0} \omega + Rm\left( {\displaystyle \omega R} \right) = \left( {\displaystyle J_{0} + mR^{2}} \right)\omega = J\omega ,$ где $J$ - момент инерции цилиндра относительно мгновенной оси вращения, $R$ - радиус цилиндра.

2. Если шару массы $m$ сообщить скорость ${\displaystyle \bf v}_{0} ,$ обеспечивающую движение по круговой орбите вокруг гравитационного силового центра O', то он будет двигаться поступательно $\left( L_{O} = 0 \right),$ а его момент импульса относительно O' $L_{O'} = mv_{0} R$ (рис. 2.20а). Если при этом шар будет вращаться вокруг собственной оси с угловой скоростью $\omega ,$ как показано на рис. 2.20б, то постоянный относительно точки O' момент импульса шара будет равен $L_{O'} = L_{O} + mv_{0} R = J_{0} \omega + mv_{0} R.$

Рис. 2.20.

Расчеты показывают, что момент импульса планет Солнечной системы относительно собственного центра масс значительно меньше их орбитального момента импульса. Орбиты всех планет лежат приблизительно в одной плоскости, так что их орбитальные моменты импульса складываются арифметически. Интересно, что все 9 планет движутся вокруг Солнца в одном и том же направлении, так что суммарный момент импульса Солнечной системы отличен от нуля.

Назад| Вперед