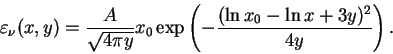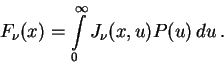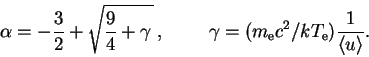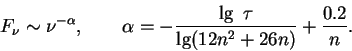|
Астронет: В. Ф. Сулейманов/КГУ Рентгеновская астрономия http://www.astronet.ru/db/msg/1174809/node6.html |
<< 4. Краткие характеристики источников | Оглавление | 6. Влияние межзвездного поглощения ... >>
5. Формирование рентгеновских спектров в процессе комптоновского рассеяния.
Процесс обмена энергией между нерелятивистскими фотонами (
![]() ) и нерелятивистскими тепловыми электронами (
) и нерелятивистскими тепловыми электронами (
![]() ) описывается уравнением
Компанейца (1956):
) описывается уравнением
Компанейца (1956):
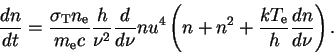 |
(15) |
| (16) |
| (17) |
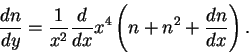 |
(18) |
- 1). Комптоновское рассеяние сохраняет число фотонов. Действительно,
- 2). Решением стационарного уравнения Компанейца (
- 3). Уравнение энергетического баланса.
| (19) |
| (20) |
| (21) |
Средняя энергия фотона в распределении Вина равна:
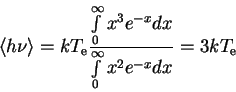 |
(22) |
Задача 2. Прямым вычислением убедиться, что распределение Б-Э
является решением стационарного уравнения Компанейца, а распределение Вина -
решением стационарного уравнения Компанейца без учета индуцированных процесов,
т.е. без члена ![]() .
.
Умножим уравнение Компанейца на
![]() и проинтегрируем его по
частоте. Интегрирование, произведенное по частям в пределах от нуля до
бесконечности дает (Левич и Сюняев, 1971):
и проинтегрируем его по
частоте. Интегрирование, произведенное по частям в пределах от нуля до
бесконечности дает (Левич и Сюняев, 1971):
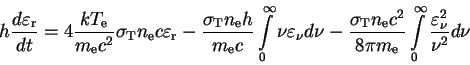 |
(23) |
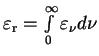 - интегральная
плотность энергии излучения. Так как при комптоновском рассеянии изменение
плотности энергии излучения равно изменению внутренней энергии электронов, то
- интегральная
плотность энергии излучения. Так как при комптоновском рассеянии изменение
плотности энергии излучения равно изменению внутренней энергии электронов, то
| (24) |
В стационарном случае
![]() , и можно найти температуру
электронов в поле излучения с заданным спектром
(Зельдович и Левич, 1970):
, и можно найти температуру
электронов в поле излучения с заданным спектром
(Зельдович и Левич, 1970):
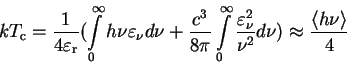 |
(25) |
Задача 3. Вывести уравнение энергетического баланса.
В том случае, когда фотоны низких энергий взаимодействуют с горячими
электронами, можно пренебречь первыми двумя членами в уравнении Компанейца, и
оно будет учитывать лишь доплеровское изменение частоты при рассеянии.
Зельдович и Сюняев (1969)
нашли решение получившегося диффузионного уравнения,
которое в случае бесконечно узкой линии имеет вид:
Отметим, что формулировка уравнения Компанейца как изменение спектра фотонов
от времени является очень удобной при рассмотрении космологических задач.
Однако при рассмотрении формирования рентгеновских спектров в стационарных
астрофизических объектах, таких как аккреционные диски, необходимо перейти
от времени к пространственной переменной. Это достаточно просто сделать,
так как введенное ранее безразмерное время является по смыслу также электронной
оптической толщой ![]() , умноженной на
, умноженной на
![]() .
Таким образом, чем большую оптическую толщу проходят фотоны, тем большее
время они подвергаются взаимодействию с электронами. В реальности картина
несколько сложнее, и время взаимодействия между фотоном и электронами
определяется числом рассеяний
.
Таким образом, чем большую оптическую толщу проходят фотоны, тем большее
время они подвергаются взаимодействию с электронами. В реальности картина
несколько сложнее, и время взаимодействия между фотоном и электронами
определяется числом рассеяний ![]() , испытанных фотоном
, испытанных фотоном
![]() . Исходя из свойств уравнения Компанейца, можно сказать,
что при большом количестве рассеяний, когда
. Исходя из свойств уравнения Компанейца, можно сказать,
что при большом количестве рассеяний, когда ![]() из среды выходит
излучение, имеющее спектральное распределение Бозе-Эйнштейна. Однако при
не очень большой оптической толще горячих электронов
из среды выходит
излучение, имеющее спектральное распределение Бозе-Эйнштейна. Однако при
не очень большой оптической толще горячих электронов ![]() имеются условия для формирования степенного спектра. Такая задача была
решена Сюняевым и Титарчуком (1980).
имеются условия для формирования степенного спектра. Такая задача была
решена Сюняевым и Титарчуком (1980).
Рассмотрим плоскопаралельный слой горячих электронов оптической толщины
![]() , через который проходит излучение низкой частоты со средней энергией
, через который проходит излучение низкой частоты со средней энергией
![]() . Среднее количество рассеяний, испытываемых фотонами
при прохождении через слой, равно
. Среднее количество рассеяний, испытываемых фотонами
при прохождении через слой, равно
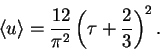 |
(27) |
Здесь
где
Здесь постоянные
Таким образом, мы видим, что в спектральной области
![]() формируется степеной спектр. Вполне очевидно, что при больших
частотах, когда начинает играть роль эффект отдачи, формируется Виновское
распределение с экспоненциальным завалом на высоких частотах.
Из формулы (30)
видно, что наклон спектра (значение
формируется степеной спектр. Вполне очевидно, что при больших
частотах, когда начинает играть роль эффект отдачи, формируется Виновское
распределение с экспоненциальным завалом на высоких частотах.
Из формулы (30)
видно, что наклон спектра (значение ![]() ) зависит от произведения
) зависит от произведения
![]() , т.е. от оптической толщины плазмы и ее электронной температуры.
Используя этот факт, можно по наклону спектра рентгеновского источника
попытаться оценить это значение. Более того, если в спектре имеется
экспоненциальный завал, то по энергии, где начинается этот завал
(
, т.е. от оптической толщины плазмы и ее электронной температуры.
Используя этот факт, можно по наклону спектра рентгеновского источника
попытаться оценить это значение. Более того, если в спектре имеется
экспоненциальный завал, то по энергии, где начинается этот завал
(![]() ), можно оценить значение температуры, и используя ее,
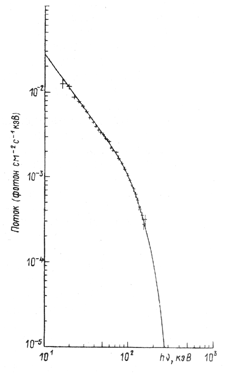
найти и оптическую толщину плазмы. Пример такой оценки дает кандидат в черные
дыры Cyg X-1. Его спектр, полученный на высотном баллоне группой Трюмпера
(Сюняев и Трюмпер, 1979)
прекрасно описывается формулой (29) с параметрами
плазмы
), можно оценить значение температуры, и используя ее,
найти и оптическую толщину плазмы. Пример такой оценки дает кандидат в черные
дыры Cyg X-1. Его спектр, полученный на высотном баллоне группой Трюмпера
(Сюняев и Трюмпер, 1979)
прекрасно описывается формулой (29) с параметрами
плазмы ![]() = 26.5 кэВ и
= 26.5 кэВ и ![]() =2 (рис. 10).
=2 (рис. 10).
Когда плазма является релятивистской, т.е.
![]() ,
уравнение Компанейца неприменимо, и неоходимы расчеты методом Монте-Карло
(Поздняков, Соболь и Сюняев, 1982)
,
уравнение Компанейца неприменимо, и неоходимы расчеты методом Монте-Карло
(Поздняков, Соболь и Сюняев, 1982)
Такие расчеты показали, что рассеяние низкочастотных фотонов в облаке
релятивистской плазмы с температурой
![]() формирует степенной спектр с показателем
формирует степенной спектр с показателем ![]() , линейно зависящим от
, линейно зависящим от
![]() , логарифма оптической толщины облака:
, логарифма оптической толщины облака:
Остроумный способ аналитической оценки показателя степени в спектре для такой
задачи был предложен Я.Б. Зельдовичем. Действительно, как отмечалось ранее,
при каждом рассеянии фотона на ультрарелятивистском электроне с энергией
![]() частота фотона возрастает в
частота фотона возрастает в ![]() раз.
Предположим, что при максвелловском распределении электронов по скоростям
энергия фотона возрастает в среднем в
раз.
Предположим, что при максвелловском распределении электронов по скоростям
энергия фотона возрастает в среднем в
![]() раз. После
раз. После ![]() рассеяний энергия возрастает в
рассеяний энергия возрастает в
![]() раз, т.е.
раз, т.е.
![]() . С другой стороны, в плазме малой оптической
толщины вероятность, что фотон испытает одно рассеяние, равна
. С другой стороны, в плазме малой оптической
толщины вероятность, что фотон испытает одно рассеяние, равна
![]() , а
, а ![]() рассеяний - по порядку величины
рассеяний - по порядку величины ![]() . Ясно, что
интенсивность излучения на частоте
. Ясно, что
интенсивность излучения на частоте ![]() пропорциональна
пропорциональна ![]() рассеяниям:
рассеяниям:
| (32) |
<< 4. Краткие характеристики источников | Оглавление | 6. Влияние межзвездного поглощения ... >>